|
Energie mécanique : physique concours ECE 08
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||
| .
. |
||||||
|
||||||
|
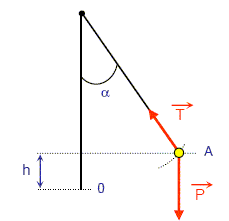
Répondre par vrai ou faux. Un pendule est constitué d’une bille de masse m fixée à l’extrémité d’un fil de masse négligeable et de longueur l. La bille est écartée de sa position d’équilibre, le fil fait un angle a avec la verticale, il est alors lâché sans vitesse initiale. On négligera la résistance de l’air et on considère que l’énergie potentielle est comptée à partir du point 0, c'est-à-dire la position la plus stable de la bille.
A- La bille en A, en équilibre, possède une énergie potentielle et une énergie cinétique nulles. Faux. La bille est lâchée sans vitesse en A : l'énergie cinétique est nulle. L'altitude du point A n'est pas nulle : l'énergie potentielle de pesanteur en A n'est pas nulle. B- L’énergie mécanique totale est Em = mg l (1-cos a). Vrai. L'altitude du point A est l(1-cos a ) ; l'énergie potentielle de pesanteur en A est : mgl(1-cos a ). L'énergie cinétique est nulle en A ; l'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle. C- Arrivée au point O, la masse m possède une énergie potentielle nulle et une énergie cinétique Ec(O) =½mv02. Vrai. D- Le travail de la tension du fil est positif. Faux. La tension est constamment perpendiculaire à la vitesse : une force perpendiculaire à la vitesse ne travaille pas.
L’ensemble est placé sur un plan incliné d’angle a = 30 ° supposé parfaitement lisse. On prendra g=10 N/Kg. travail résistant du poids en
montée : W = -mgd sin a
= -0,030*10*0,8 * sin 30 = -0,12 J. Energie minimale du joueur : 0,12 J. énergie potentielle élastique : ½kx2 = 0,5*120*x2 = 0,12 ; x2 = 2 10-3 ; x ~ 0,045 m ~ 4,5 cm. C- On peut négliger la valeur x devant la distance d. Vrai. x/d~ 4/80 = 0,05 ( 5 %) D- La vitesse initiale de propulsion pour que la bille atteigne le point d est v= 28 m/s. Faux. Conservation de l'énergie mécanique : ½mv2= 0,12 ; 0,5*0,03v2 = 0,12 ; v2 = 8 ; v ~ 2,8 m/s.
Un homme, de masse m=70 kg, fait un saut à l'élastique du haut d'un pont de pierre élevé. Le tablier du pont est situé à une hauteur de 60 m au dessus du fond de la vallée, l'élastique a une longueur de 15 m et son extrémité est accrochée sur la partie inférieure de l'arche du pont, 5 m sous l'endroit où se tient l'homme et d'où il saute. On choisit enfin la position de l'homme avant le saut comme niveau de référence de l'énergie potentielle gravitationnelle, et on prend g=10 N/kg. Au cours de la chute, l'élastique commence à se tendre au point A. A- L'énergie potentielle de l'homme vaut 28 kJ quand il est en A. Faux. altitude de A : hA = -20 m ; énergie potentielle de pesanteur : mghA =70*10*(-20) =-14 kJ. B- La vitesse du centre d'inertie de l'homme en A vaut 10 m s-1. Faux. Energie mécanique à la position de l'homme avant le saut : 0 Energie mécanique de l'homme en A : mghA +½mv2. l'énergie mécanique se conserve : mghA +½mv2. =0 ; -14000 +35 v2=0 ; v2=400 ; v = 20 m/s. L'élastique atteint sa tension maximale en B, on indique que sa longueur vaut alors 45 m. C- La raideur de l'élastique est donc de 178 N /m. Faux. allongement : 45-15 = 30 m. Si la tension maximale est atteinte, l'homme ne descendra pas plus bas : sa vitesse et en conséquence son énergie cinétique sont nulles. Energie mécanique de l'homme en B : mghB +½kx2. l'énergie mécanique se conserve : mghB +½kx2 =0 70*10*(-50) + 0,5 k *302 = 0 ; -35000+450 k =0 ; k ~ 78 N/m. D- Juste après le point B le mouvement de l'homme est uniforme. Faux. L'homme commence à remonter ; sa vitesse va croître puis décroître. Dans un mouvement uniforme, la valeur de la vitesse est constante.
Un pendule simple est constitué par une petite masse m= 100 g suspendue à l'extrémité d'un fil inextensible de longueur l=40 cm. On écarte le fil de sa position d'équilibre d'un angle a0 = 9° puis on le lâche sans vitesse initiale. Le plan horizontal contenant la position d'équilibre du solide est choisi comme plan de référence où l'énergie potentielle de pesanteur est nulle. On donne cos 9 = 0,99 ; sin 9 = 0,14 ; 2½ =1,4 ; g = 10 m s-2. A- La période du pendule T = 12,5 s . Faux. T = 2 pi (L/g)½ = 6,28 (0,4/10) ½ =6,28*(0,04) ½ =6,28*0,2 =1,25 s. B- L'énergie mécanique du pendule est de 4 J. Faux. E = mgL(1-cos a0 ) =0,1*10*0,4 (1-0,99) = 0,4*0,01= 4 10-3 J = 4 mJ. C- La vitesse maximale de l'objet est d'environ 2,8 m/s. Faux. Conservation de l'énergie mécanique : 4 10-3 = ½mv2max ; v2max = 8 10-3 /0,1 = 2*4 10-2 ; vmax =1,4*0,2 =0,28 m/s. D- Lorsque l'énergie cinétique du pendule est égale au quart de son énergie mécanique, la vitesse de la masse est égale à la moitié de sa vitesse maximale. Vrai. 10-3 =½mv2 ; v2 = = 2 10-3 /0,1 = 2 10-2 ; v =1,4*0,1 =0,14 m/s.
|
||||||
|
|
||||||
|
|