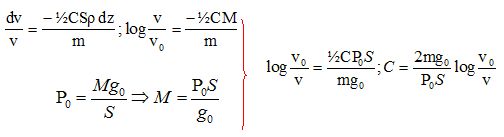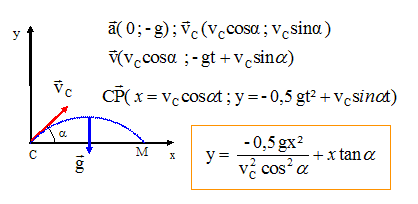|
Chute verticale, projectile : physique concours ECE 08
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||
| .
. |
||||||
|
||||||
|
Répondre par vrai ou faux. Un parachute de 80 kg a sur le dos un parachute de masse 20 kg. Il saute hors d’un avion en vol. Au début du saut, la pression atmosphérique est très faible: l'air est raréfié et son action sur le parachutiste peut être négligée. On prendra g = 10 m s-2. A- Pendant cette première phase, le parachutiste a une vitesse de chute constante. Faux. Le parachutiste n'est soumis qu'à son poids : mouvement de chute libre sans vitesse initiale : v = gt. Une fois le parachute ouvert, celui-ci est soumis à la résistance de l’air, assimilable à une force de frottement de module F= k v2 avec k = 20 kg m-1. B- La vitesse limite vlim atteinte par le parachutiste est v2lim =(M+m)g/k. Vrai. On néglige la poussée d'Archimède due à l'air. Quand la vitesse limite est atteinte le mouvement est rectiligne uniforme : le poids et la force de frottement se neutralisent. (M+m)g = k v2lim. C- Elle est donc d’environ 25 km.h-1. Vrai. v2lim= (M+m)g / k = 100*10/20 = 50 ; vlim~ 7,1 m/s = 7,1*3,6 km/h ~ 25 km/h. D- Pour arriver au sol avec la même vitesse lim V , mais en chute libre il suffirait de partir de la hauteur 2,5 m à vitesse initiale nulle. Vrai. On choisit un axe vertical, orienté vers le bas ; l'origine est choisie à l'altitude initiale. v = gt ; t = v/g = 7,1/10 = 0,71 s ; z = ½gt2 = 0,5*10*0,712 ~2,5 m.
- FA, la
poussée d'Archimède, verticale,
orientée vers le haut, - P son
poids, - f , la force de
frottement de l'air sur le système,
verticale, orientée vers le bas qui est
négligeable au début du
mouvement.
Vrai. rair Vb g -Mg > 0 soit M < rair Vb. Vrai. La poussée d'Archimède est supérieure au poids pour qu'il y ait décollage. On accroche une nacelle de masse m=200 g pour transporter du matériel météo de masse m’ à ce ballon. C- La masse maximale m’ de matériel scientifique que l'on peut embarquer dans la nacelle est de 9,8 kg. Vrai. Valeur de la poussée d'Archimède rair Vb g = 1,2*10 g = 12 g. Poids total (M+ m+m')g = (2,2+m')g. La poussée d'Archimède doit être supérieure au poids pour qu'il y ait décollage : 12 > 2,2+m' ; m' < 9,8 kg. D- L’équation différentielle régissant le mouvement du ballon peut se mettre sous la forme : dv/dt = Av2 +B avec A = -krair/M et B = [rairVb/M-1]g. Système : ballon + nacelle et matériel. Faux.
Système : ballon sans nacelle sans matériel : m + m' = 0. Vrai.
Un obus de masse m est propulsé à partir d’un canon avec une vitesse initiale v0 . On note r la masse volumique de l'air qui dépend de l'altitude z, v la vitesse de l'obus, S la section droite de l'obus. La force F de freinage est du type F=½C S r v2 où C est une constante dépendant de la forme de l'obus, l'atmosphère ayant une épaisseur h de 10 km. On considère que la pression atmosphérique au sol est P0 = 105 Pa et g0= 10 m s-2. On étudie le système sur les premiers kilomètres où l’on peut considérer le poids de l'obus comme étant négligeable par rapport à la force de freinage. A- La seconde loi de Newton se réduit à dV/dt= -F/m. Vrai.
B- On a la relation suivante entre la variation de la vitesse et d’altitude dv/v = - CSr /(2m) dz. Vrai. C-
La masse M d'une colonne d'air de
section S comprise entre le sol et une altitude infinie
s’écrit : D- La constante C de la force de freinage s’exprime en fonction de la vitesse initiale v0, de la vitesse finale v après traversée de l'atmosphère et des autres données sous la forme : C =2mg0/(P0S) ln( v0/v). Vrai.
On laisse tomber sans vitesse initiale, d'une hauteur h = 1,80 m, deux corps différents, une bille Bl métallique, de masse m1 = 0,7 kg, et une bille plus légère, B2, de masse m2 = 0,056 kg. On admet l’existence d’une force supplémentaire de frottement visqueux proportionnelle à la vitesse de valeur f = a v ; a = m / t = 14 10-6 S.I. A- La vitesse v d’une bille satisfait à l’équation différentielle dv/dt - v/t=g selon la verticale descendante Ox. Faux. La bille est soumise à son poids et à la force de frottement visqueux ; la seconde loi de Newton s'écrit suivant un axe vertical descendant : mg - a v = m dv/dt ; mg - m v / t = m dv/dt ; g - v / t = dv/dt ; dv/dt + v / t = g. On considère que v(t) = g t [ 1- exp(-t/t) ] vérifie convenablement l’équation de mouvement de chute de ces billes. B- L'équation horaire est x(t) =g t [ t + t + t exp(-t/t) ]. Faux. La position est une primitive de la vitesse : x(t) = g t [ t + t exp(-t/t) ] + constante. A t = 0, x(0) =0 : 0 = g t [ 0 + t ] + constante ; constante = -gt2. x(t) = g t [ t - t + t exp(-t/t) ]. C- Une expression approchée de x(t) pour t << t est x(t) = ½ gt2, comme s'il n'y avait pas de frottement. Vrai. exp(-t/t) ~ 1 ; x(t) ~ g t [ t - t + t ] ~g t t. Au début de la chute, la vitesse est faible ; la force de frottement étant proportionnelle à la vitesse, celle-ci peut être négligée devant le poids : la chute est libre. D- Lorsque la force de frottement est faible, la durée de chute est de 0,6 s et est identique pour les deux billes. Vrai. La chute est libre : 1,8 = 5 t2 ; t2 = 1,8/5= 0,36 ; t = 0,6 s.
|
||||||
|
|
||||||
|
|
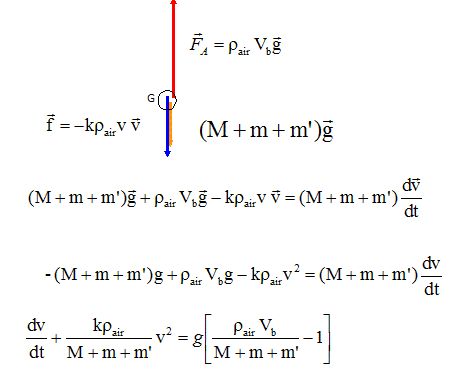
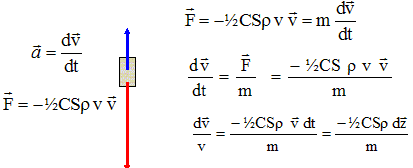
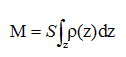 .
Vrai.
.
Vrai.