La lumière : diffraction, réfraction : physique concours ECE 08 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

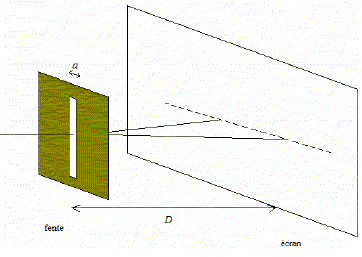
Répondre par vrai ou faux. On utilise un laser à CO2 produisant une lumière de longueur d’onde l comprise entre 9 micromètres et 11,5 micromètres placé devant une fente de largeur a et d’un écran. A- les limites des longueurs d’onde du domaine du visible sont 600 nm < l <800 nm. Faux. 400 nm à 800 nm. B- les radiations du laser utilisé appartiennent au domaine des U. V. Faux. 9 micromètres à 11,5 micromètres, valeurs supérieures à 0,8 micromètres ( 800 nm) : domaine des infrarouges. On observe la figure suivante, constituée de tâches lumineuses, sur l’écran placé à une distance D de la fente. C- On observe un phénomène d’interférences. Faux. diffraction par une fente de largeur voisine de la longueur d'onde de la lumière. D- La taille de la fente doit être de l’ordre de grandeur de la longueur d’onde pour que l’on obtienne cette figure. Vrai. On considère un prisme, d’arrête A , constitué d’un verre d’indice n pour une radiation jaune. On fait arriver une radiation jaune sur la face d’entrée du prisme sous une incidence i. A-Les radiations bleues seront moins déviées que des radiations jaunes. Faux. 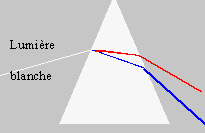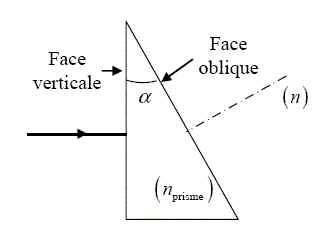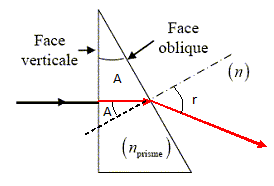Les radiations bleues sont les plus déviées. B- La déviation D totale du rayon incident après la traversée du prisme est inversement proportionnelle à l’indice n. Faux. La déviation D varie dans le même sens que l'indice n. C- En passant du jaune au bleu, la longueur d’onde augmente. Faux. En passant du jaune ( ~ 630 nm ) au bleu (~ 400 nm) , la longueur d’onde diminue. D- La radiation de la lumière rouge est l = 486 nm. Faux. Dans le vide la longueur d'onde de la lumière rouge est voisine de 700 nm. On utilise un laser à CO2 produisant une lumière de longueur d’onde l comprise entre 9 micromètres et 11,5 micromètres placé devant une fente de largeur a et d’un écran située à une distance D. On fait varier la largeur a de la fente tout en maintenant tous les autres paramètres constants et on mesure les dimensions de la tache centrale d correspondantes. On sait que d est proportionnelle à la longueur d’onde de la lumière et à la distance fente écran. 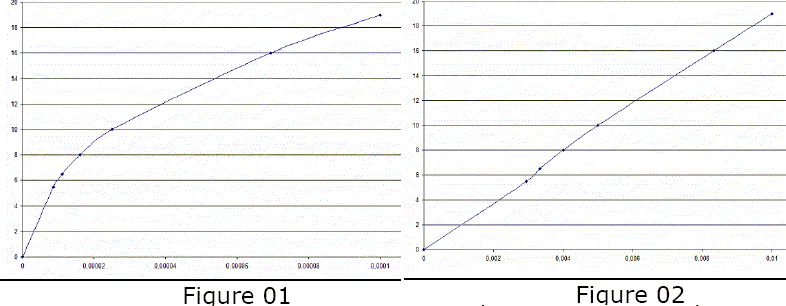On peut alors représenter les courbes suivants : La figure 01 représente la distance d (en mm) fonction de 1/a2 ( en mm-2) ; la figure 02 représente la distance d (en mm) fonction de 1/a en mm-1. A- Une analyse de ces courbes permet d’écrire que : d = AlD/a2 avec A étant une constante sans dimension. Faux. la figure 02 indique que d est proportionnelle à 1/a et on sait que d est proportionnelle à la longueur d’onde de la lumière et à la distance fente écran. d'où : d = AlD/a. 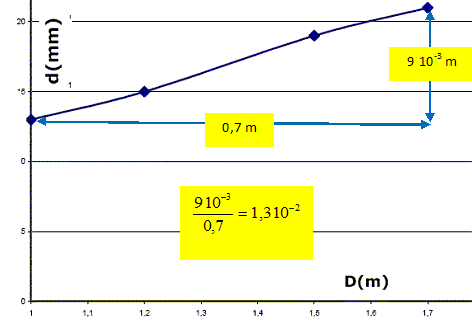On fixe l et a et on fait varier D, on obtient la courbe ci-dessous permettant de vérifier la relation entre d et D .   B- le coefficient directeur a de la droite est d’environ 15 10-3. Vrai. On effectue des mesures pour l = 600 nm et a = 100 micromètres. C- on trouve la constante de proportionnalité A=1,8. Faux. d = AlD/a ; d /D~ 13 10-3 ; l = 6 10-7 m ; a = 10-4 m. A = ad / (lD) = 10-4 *15 10-3 / 6 10-7 =13/6 ~ 2. On dispose d'un autre laser de longueur d’onde l = 700 nm pour mesurer le diamètre a d’un fil placé sur le support et on obtient une tâche centrale de largeur d = 20 mm lorsque l’écran est à D = 1,50 m du fil en prenant comme valeur pour la constante A la valeur 2. D- Le diamètre du fil est de 115 micromètres. Faux. d = AlD/a ; a = AlD/d = 2*7 10-7*1,5 /2 10-2 = 10,5 10-5 m= 105 micromètres. Un laser rouge He-Ne émet à la longueur d'onde 0,6 micromètre dans le vide. Sa puissance est de 0,5 mW. La vitesse de propagation de la lumière dans le vide est c= 3 108 m/s ; pi ~ 3. 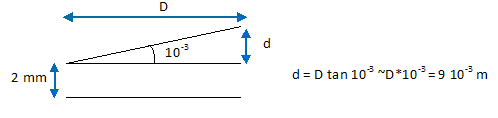A- La fréquence f de la radiation émise est de 0,5 1014 Hz. Faux. f = c/l = 3 108 / 6 10-7 =0,5 1015 Hz. A sa sortie du tube, le faisceau a un diamètre d = 2 mm et il a un demi-angle de divergence de 1 mrad. B- Le diamètre de la tache produite sur un écran placé à D=9 m est de 2 mm. Faux. diamètre= 2 d+ 2 10-3 = 2 10-2 m = 2 cm. C- La surface couverte sur l’écran est de 3.10-6 m2. Faux. S = pi d2/4 = 3*(2 10-2)2/4 =3 10-4 m2. D- La puissance lumineuse reçue par l'écran est d’environ 1,67 W m-2. Vrai. 5 10-4 / 3 10-4 ~1,67 W m-2. Un faisceau lumineux atteint en incidencenormale la face verticale d’un prisme d’angle au sommet A. L’indice de l’air est égal à 1. L’indice du prisme est noté nprisme . On note (n) la normale à la face oblique. On donne les valeurs suivantes des sinus : i ° 5 10 15 20 25 30 35 40,5 45 50 60 70 80 sin i 0,09 0,17 0,26 0,34 0,42 0,5 0,57 0,65 0,71 0,76 0,87 0,94 0,98 A- Le rayon incident n’est pas dévié à la traversée de la face verticale. Vrai. angle d'incidence i =0 ; sin 0 = 0 ; loi de Descartes pour la réfraction nair sin i = nprisme sin i2. 1*sin 0 = nprisme sin i2 : 0 = nprisme sin i2 d'où sin i2 = 0 ; i2 = 0. B- Avec nprisme = 4 /3 , le rayon émergent de la face oblique fait l’angle A avec (n) , la normale à la face de sortie. Faux. nprisme sin A = nair sin r ; 4/3 sin A = sin r. C- Avec nprisme = 4 /3 et A = 40,5° le rayon émergent de la face oblique fait l’angle de 40,5° avec (n) , la normale à la face de sortie. Faux. 4/3 sin A = sin r ; 4/3 sin 40,5 = sin r ; 4/3*0,65 = sin r ; sin r = 0,87 ; r = 60°. D- Avec A =30° et un rayon émergent faisant un angle de 45° avec (n), nprisme = 1,42. Vrai. nprisme sin A = nair sin r ; nprisme sin 30 = sin 45 ; nprisme *0,5 = 0,71 ; nprisme = 1,42. E- Avec nprisme = 1,5 et et un rayon émergent faisant un angle de 60° avec (n), A est de l'ordre de 35°. Vrai. nprisme sin A = nair sin r ; 1,5 sin A = sin 60 ; 1,5 sin A = 0,87 ; sin A =0,87/1,5 = 0,58 ; A ~ 35°.

retour -menu