Hydroxyde de zinc, ion tétrahydroxozincate concours caplp interne 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Dans un becher contenant une solution de chlorure de zinc de concentration initiale 0,01 mol/L, on ajoute goutte à goutte une solution d'hydroxyde de sodium de concentration 1 mol/L. On observe tout d'abord l'apparition d'un précipoté d'hydroxyde de zinc (II) qui fini par disparaître complétement lorsque la quantité d'hydroxyde de sodium ajoutée est suffisante. L'hydroxyde de zinc a réagi avec les ions hydroxydes pour donner l'ion complex Zn(HO)42-. La variation du volume de la solution est considérée comme négligeable. Zn2+ + 4HO- = Zn(HO)42- avec log K3 = 15,3 ( K3 constante de formation du complexe) Définir un ion complexe. Expliquer la formation de l'ion tétrahydroxozincate (II) et sa géométrie. Un complexe est un édifice polyatomique comprenant un cation central entouré de plusieurs ligands ( molécules ou ions ) ; ces derniers délocalisent une partie de leur densité électronique sur le cation central. L'ion tétrahydroxozincate (II) est tétraèdrique ( type AX4) Q'appelle t-on indice de coordination ? Donner l'indice de coordination de l'ion tétrahydroxozincate (II). Le nombre de coordination est égal au nombre de liaisons sigma entre les ligands et l'atome central. ( 4 dans le cas présent) Donner 3 exemples d'applications dans lesquelles la formation des complexes est utilisée. - Solubiliser un métal contenu dans un minerai ( l'or est solubilisé comme un complexe cyanuré) - Caractériser la présence d'une espèce chimique par formation d'un complexe coloré. - Des complexes de platine sont utilisés dans le traitement de certains cancers (cisplatine, carboplatine, oxaliplatine…). - La capacité complexante de l'EDTA est mise à profit dans le traitement d'intoxication par des métaux, - Les complexes métalliques sont extrêmement utiles en catalyse.   Formation des complexes. Ecrire l'équation de la formation du précipité d'hydroxyde de zinc. Donner l'expression de la constante d'équilibre K1. Zn2+ + 2HO- = Zn(OH)2 (s) ; K1 = 1/ ([Zn2+][HO-]2). Ecrire l'équation de la réaction de dissolution du précipité d'hydroxyde de zinc (II). Donner l'expression de la constante d'équilibre K2. Zn(OH)2 (s) + 2HO- = Zn(OH)42- ; K2 = [Zn(OH)42-]/ [HO-]2. Donner l'expression de la constante globale d'équilibre K3 de la réaction de formation de Zn(OH)42-. Donner la relation liant les trois constantes d'équilibre. Zn2+ + 4HO- = Zn(HO)42- avec log K3 = 15,3 ( K3 constante de formation du complexe) K3= [Zn(OH)42-]/ ([HO-]4[Zn2+]) avec K1 K2 = K3. Calcul des constantes d'équilibre. Ecrire l'expression du produit de solubilité de l'hydroxyde de zinc. Donner sa valeur. Zn(OH)2 (s) =Zn2+ + 2HO- ; Ks = [Zn2+][HO-]2. On donne pKs = 16,3 ; Ks = 10-16,3 = 5,0 10-17. Calculer la valeur de chaque constante d'équilibre. K1 = 1/Ks = 1016,3 = 2,0 1016 ; K3 = 1015,3 =2,0 1015 ; K2 = K3 / K1 =2,0 1015 /2,0 1016 = 0,1. Calcul des valeurs de pH lors de la formation et de la dissolution du précipité. Calculer la valeur du pH à partir de laquelle le précipité d'hydroxyde de zinc apparaît. Le précipité d'hydroxyde de zinc apparaît dès que [Zn2+][OH-]2=10-16,3. " Dans un becher contenant une solution de chlorure de zinc de concentration initiale 0,01 mol/L..." A ce moment [Zn2+] =10-2 molL-1 et [OH-]=racine carrée( 10-16,3/10-2) = 7,1 10-8 mol L-1. pH = 14 + log( 7,1 10-8 )= 6,9. Calculer la valeur du pH à partir de laquelle le précipité d'hydroxyde de zinc est totalement transformé en ion Zn(OH)42-. Le précipité d'hydroxyde de zinc disparaît dès que tous les ions Zn2+ sont engagés dans le complexe [Zn(OH)4] 2- c'est à dire [Zn(OH)4] 2- =10-2 mol L-1. Zn(OH)2 (s) + 2HO- = Zn(OH)42- ; K2 = [Zn(OH)42-]/ [HO-]2. [HO-]2 = [Zn(OH)42-]/K2 = 10-2/0,1 = 0,1 ; [HO-] =0,1½ =0,316 pH = 14 + log( 0,316) = 13,5. 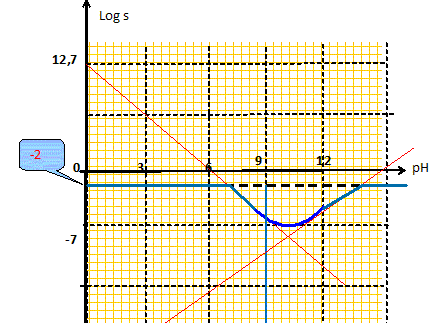Diagramme de prédominance des ions. Déterminer l'expression des concentrations [Zn2+] et [Zn(OH)42-] en fonction de la concentration en ion H+ si la solution est saturée. d'une part : Zn(OH)2(s) = Zn2+ + 2HO-  Ks=[Zn2+][HO-]2 = [Zn2+]Ke2 / [H+]2 soit [Zn2+]= Ks[H+]2 / Ke2 = 10-16,3 / 10-28 [H+]2 =1012,7 [H+]2. Zn(OH)2 (s) + 2HO- = Zn(OH)42- ; K2 = [Zn(OH)42-]/ [HO-]2 = [Zn(OH)42-]Ke2 / [H+]2 [Zn(OH)42- ] = K2 10-28/[H+]2/= 10-29/[H+]2. Calculer la valeur du pH pour laquelle [Zn2+] = [Zn(OH)42-]. 1012,7 [H+]2 = 10-29/[H+]2 ; [H+]4 = 10-29 /1012,7 = 10-41,7 ; [H+] =3,75 10-11 ; pH =10,4. Calculer la valeur du pH pour laquelle la solubilité est minimale. s = [Zn2+] + [Zn(OH)42-] =1012,7 [H+]2 +10-29/[H+]2 ; dériver : ds/d[H+] = 2 1012,7 [H+] -2 10-29/[H+]3 cette dérivée s'annule pour [H+]4 = 10-29/1012,7 [H+] =3,75 10-11 ; pH =10,4. Quelle est la valeur de cette solubilité minimale ? s = [Zn2+] + [Zn(OH)42-] =1012,7 [3,75 10-11]2 +10-29/[3,75 10-11]2 = 1,4 10-8 mol/L. Tracer log s = f(pH) et commenter. log s =log [1012,7 [H+]2 +10-29/[H+]2 ] en milieu acide ( pH <5) : log s ~ log(1012,7 [H+]2 ) ~ 12,7 -2pH. en milieu basique ( pH >11) : log s ~ log (10-29/[H+]2 ) ~ -29 +2pH. On plonge un morceau de grenaille de zinc dans la solution saturée d'hydroxyde de zinc (II). Ecrire les deux équilibres dont la grenaille de zinc est le siège. Zn(s) = Zn2+ + 2e- (1) ; Zn(s) +2HO- = Zn(OH)2 (s) + 2e- (2). Ecrire les deux expressions de la loi de Nernst pour l'électrode ainsi constituée et établir la relation entre Ks, E°(Zn2+/Zn) et E°( Zn(OH)2/Zn ). E =E°(Zn2+/Zn) +0,03 log[Zn2+] avec  Ks=[Zn2+][HO-]2 ; E =E°(Zn2+/Zn) +0,03 log(Ks/[HO-]2) = E°(Zn2+/Zn) +0,03 log(Ks) + 0,03 log (1/[HO-]2) d'autre part : E = E°( Zn(OH)2/Zn ) + 0,03 log (1/[HO-]2) Par identification : E°(Zn2+/Zn) +0,03 log(Ks) = E°( Zn(OH)2/Zn ). Calculer le potentiel de l'électrode de zinc si pH = 9. E°( Zn(OH)2/Zn ) = -0,762 + 0,03 log (5,0 10-17) = -1,25 V. E = E°( Zn(OH)2/Zn ) + 0,03 log (1/[HO-]2) = -1,25 + 0,03 log ( 1/10-10) = -0,95 V.

retour -menu