du monophasé au triphasé concours caplp interne 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Extrait d'un sujet de bac professionnel : Une bobine (R, L) assimilable à une bobine parfaite d'inductance L, en série avec une résistance R. Cette bobine est alimentée sous une tension sinusoïdale u(t), de valeur efficace égale à 24 V. Elle est traversée par un courant d'intensité i't), de valeur efficace I =0,24 A. Le diagramme de Fresnel lié au fonctionnement de la bobine est donné ci-dessous : f = 50 Hz. Mesurer au rapporteur la valeur du déphasage entre l'intensité du courant et la tension, représentés par les vecteurs associés. Calculer l'échelle de représentation de U si la mesure de la norme de ce vecteur est 4,8 cm. Indiquer parmi les grandeurs i(t) et u(t), celle qui est en avance sur l'autre. Calculer l'impédance de la bobine (R, L) Calculer la puissance électrique ( puissance active) absorbée par la bobine. Rédiger une solution de cet exercice et donner les expressions de i(t) et u(t). Déphasage : j ~ 15° = p/12 radians. u(t) est en avance sur i(t). 4,8 cm dcorrespondent à 24 V soit 1 cm correspond à 5 V. Impédance de la bobine Z = U/I = 24/0,24 = 100 ohms. Puissance active = UI cosj = 24*0,24*cos15 =5,6 W. i(t) = 0,24 *2½ cos ( 314 t) ; u(t) = 24 *2½ cos ( 314 t+ p /12). Un récepteur (R, X) est assimilé à un dipôle purement résistif de résistance R en série avec un dipôle purement réactif de réactance X. Il est alimenté par une tension sinusoïdale u(t) = 325 sin(100pt-p/3) et est traversé par un courant d'intensité i(t) = 9,6 sin(100pt-p/18). Ces grandeurs sont données dans le systéme internationnal. Représenter avec soin le diagramme de Fresnel. Déterminer les valeurs des puissances apparente, active et réactive mises en jeu par le dipôle. U = 325 /2½ ; I = 9,6 /2½ ; UI = 325*9,6/2 =1560 ; S = UI = 1560 VA = 1,56 kVA. P = UI cos (-5p/18) = 1,0 kW ; Q = UI sin(-5p/18) = -1,2 kvar. Déterminer les valeurs de R et X. P= RI2 avec I2 = 9,62/2 =46,1 ; R = 1000 / 46,1 = 21,7 ohms. tan (-5p/18) = X/R ; X = -21,7 * 1,19 = -25,9 ohms. Indiquer la nature de la réactance. Calculer la capacité du condensateur ou l'inductance de la bobine qui en est la source. La tension u(t) est en retard sur i(t) : la réactance est un condensateur. 1/(Cw)= 25,9 avec w = 50*2*3,14 = 314 rad/s. C = 1/(25,9*314) = 1,2 10-4 F. Tension triphasée et transport du courant électrique. Un atelier peut être alimenté depuis un transformateur par une ligne monophasée ( 2 câbles de cuivre, la résistance de chaque câble est notée RM) ou par une ligne triphasée ( 3 câbles de cuivre, la résistance de chaque câble est notée RT). Des quantités identiques de cuivre sont utilisées pour fabriquer la ligne monophasée et la ligne triphasée. Calculer le rapport RT/RM. Les câbles ont la même longueur L ; la section des câbles de la ligne monophasée est notée SM, celle de la ligne triphasée est notée ST. Volume du cuivre : 2L SM = 3 L ST ; SM = 1,5ST. Résistance d'un câble : RT = rL/ST ; RM = rL/SM =rL/(1,5ST ) ; RT/RM = 1,5. L'atelier consomme une puissance active P et possède un facteur de puissance de valeur cos j. Donner l'expression des pertes par effet Joule PM et PT dans chacune des lignes. Calculer le rapport PT/PM. Conclure. Résistance de la ligne monophasée : 2RM ; pertes en ligne : PM=2RM IM2. Résistance de la ligne triphasée : 3RT =3RM*1,5 = 4,5RM ; pertes en ligne : PT=4,5RM IT2. Puissance active dans l'installation triphasée : P = 3½U IT cos j. Puissance active dans l'installation monophasée : P =U / 3½ *IM cos j. d'où 3IT =IM ; PM=2RM IM2 = 18RM IT2 Les pertes joule sont 4 fois plus grande dans le cas de la ligne monophasée, par rapport à la ligne triphasée. 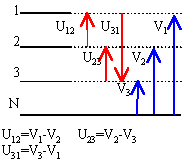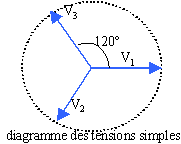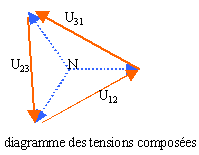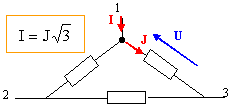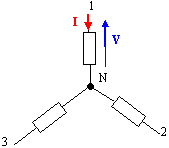Système triphasé de tension. Donner la définition d'un système triphasé de tensions. Quand dit-on qu'un système est équilibré ? Le triphasé est un système composé de trois tensions sinusoïdales, ayant même fréquence et en général la même amplitude ; ces tensions sont déphasées entre elles de 120 °. Lorsque les trois conducteurs sont parcourus par des courants de même valeur efficace, le système est dit équilibré. Un réseau triphasé comporte 3 fils de phase et un neutre. La figure 1 représente les 3 fils de phases numérotés 1, 2, 3 et le neutre N. les tensions v(t) entre fil de phase et neutre sont les tensions simples, ayant même valeur efficace V, déphasées de p/3 ( 120°) ; les tensions entre fils de phases u(t) sont appelées tensions composées : elles ont même valeur efficace U et sont déphasées de p/3 ( 120°) les vecteurs de Fresnel associés à ces tensions sont représentés sur les figure 4 et 3.   figure 1 figure 2   figure 3 figure 4 L'oscillogramme de la tension instantanée V1(t) est visualisée sur l'écran d'un oscilloscope. Représenter les traces que laisserait la tension V2(t) ainsi que la tension U12(t). Justifier. V2(t) présente un retard de 120 ° par rapport à V1(t). U12(t) = V1(t) -V2(t). Il existe deux façons de coupler des récepteurs sur un réseau triphasé. Représenter par des schémas les couplages qu'il est possible de réaliser. montage triangle montage étoile Le fil de neutre est indispensable dans le montage étoile non équilibré. Etude d'un cas. Un système triphasé de tensions équilibré (230 V / 400 V, 50 Hz) alimente un récepteur triphasé équilibré couplé en triangle. Chaque récepteur monophasé est équivalent à une résistance R= 30 ohms en série avec une inductance L= 0,07 H. Donner la signification des grandeurs 230 V / 400 V, 50 Hz. 230 V : tension simple entre phase et neutre ; 400 V : tension composée entre phases f=50 Hz : fréquence. Donner l'expression de l'impédance complexe d'un des récepteurs monophasés. Z = R + jLw avec w = 2pf = 314 rad/s Calculer les valeurs de l'impédance et de l'angle de déphasage. Z = [R2+(Lw)2]½ = [302+(0,07*314)2]½ =37,2 ohms. tan j = Lw / R = 0,07*314 / 30 =0,733 ; j = 36,2 °. Calculer l'intensité des courants qui parcourent les récepteurs et l'intensité des courants en ligne. intensité du courant dans un récepteur : J = U/Z = 400 / 37,2 =10,8 A. intensité du courant en ligne : I = 3½J =18,6 A. Calculer les puissance active, réactive et apparente. P = 3½UI cosj = 3½ *400*18,6 cos 36,2 =10,4 kW. Q = 3½UI sinj = 3½ *400*18,6 sin 36,2 =7,6 kvar. S = 3½UI =12,9 kVA. Préciser un schéma de montage avec un ou plusieurs wattmètres qui permettrait de vérifier expérimentalement la valeur de la puissance active. méthode des deux wattmètres : montage triangle ou étoile P1 = UI cos ( I1, U13) = UI cos ( -30 +j) ; P2 = UI cos ( I2, U23) = UI cos ( +30 +j) P1 + P2 =UI [cos ( -30 +j) +cos ( 30 +j)] P1 + P2 = 2UI cos j cos 30 = 3½UIcos j =P On considère que le facteur de puissance est égal à 0,8. Pour ramener ce facteur à 1, le circuit précédent est complété par une batterie de condensateurs montés en étoile. Faire le schéma du montage. 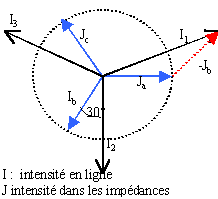Calculer la capacité des condensateurs qui ramèneront à 1 la valeur du facteur de puissance. puissance réactive des condensateurs : Q1= - 3 Cw U²= -7,6 103. tension aux bornes des condensateurs : 230 V ; C = 7,6 103 /(3*2302*314) =1,5 10-4 F. On préfère montés les condensateurs en triangle (tension aux bornes 400 V) : les capacités sont trois fois plus faibles. Calculer la puissance active P. Les condensateurs ne consomment pas de puissance active ; P reste donc inchangée ( 10,4 kW). Calculer l'intensité des courants en ligne. P= 3½UI ; I = 10,4 103 / (3½ *400) = 15 A. Calculer l'intensité des courants dans chaque récepteur monophasé et l'intensité des courants dans les condensateurs. I : intensité en ligne, I1 intensité dans un condensateur, I2 intensité dans un récepteur monophasé. I1 sin 60 = I2 sin 36,2 ; 0,866 I1 = 0,59 I2 ; I1 =0,682 I2 ; 15 = I1 cos60 + I2 cos36,2 ; 15 = 0,5 I1 + 0,8 I2 ; 15 = (0,341+0,8)I2 ; I2 =13 A ; I1 =8,9 A.

retour -menu