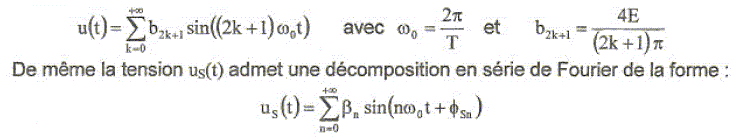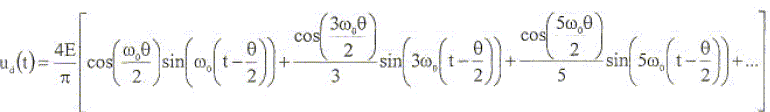Etude d'un onduleur, série de Fourier, nombres complexes concours physique Capes 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

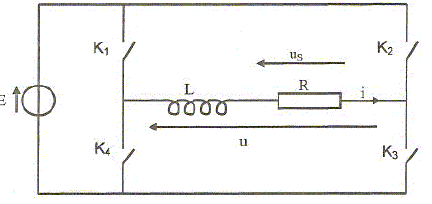
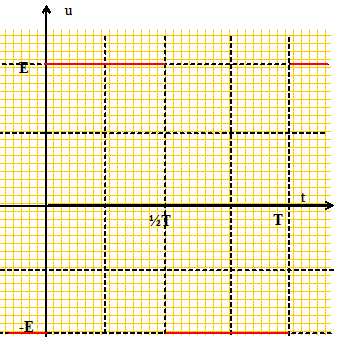
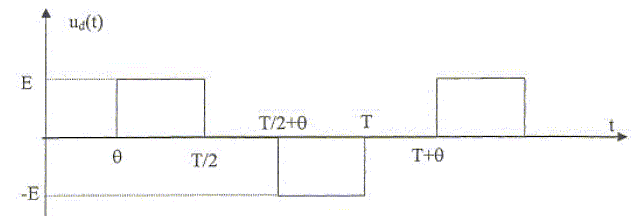
Cette partie étudie un onduleur de tension autonome à commande symétrique ou décalée. Un onduleur est un convertisseur de tension alternative. Le montage est celui représenté sur la figure ci-dessous : les quatre interrupteurs bidirectionnels K1, K2, K3, K4 sont commandés électriquement de telle façon que : pour nT< t < (n+½)T K1 et K3 fermés K2 et K4 ouverts pour (n+½) T< t < (n+1)T K1 et K3 ouverts K2 et K4 fermés Le générateur est une source de tension idéale de f.e.m E constante. L est une inductance pure dite de lissage et R représente la charge. Tracer la courbe u(t) en indiquant les points remarquables. Ecrire l'équation différentielle vérifiée par i(t), courant circulant dans la charge. 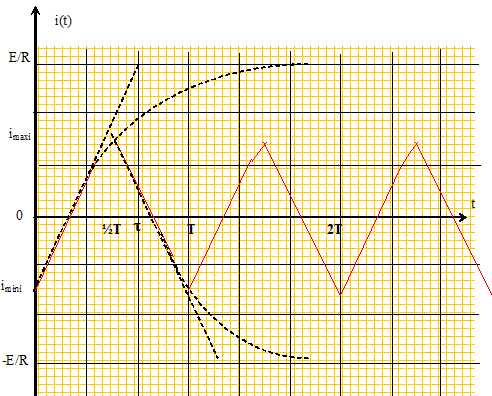u(t) = Ldi/dt +Ri avec u(t) = E si nT< t < (n+½)T et u(t) = -E si (n+½) T< t < (n+1)T Si i1(t) est la solution de cette équation pour 0 < t< ½T et i2(t) la solution de cette équation pour ½T < t < T, Déterminer les expressions de i1(t) et i2(t) en fonction de R, L et E et en fonction des deux constantes d'intégration A1 et A2 ( que l'on ne cherchera pas à calculer pour l'instant). On pose t = L/R.  nT< t < (n+½)T : solution particulière i1 = E/R ; solution gnérale de di/dt+ 1/t i =0 : i1 (t) =A1 exp(-t/t). i1(t) = A1 exp(-t/t) +E/R. (n+½) T< t < (n+1)T :solution particulière i2 = -E/R ; solution gnérale de di/dt+ 1/t i =0 : i2 (t) =A2 exp(-t/t). i2(t) = A2 exp(-t/t) -E/R. On se place en régime permanent et on cherche à déterminer les valeurs de A1 et A2. On pose a = exp(-T/(2t)). Ecrire la condition de raccordement pour le courant t = ½T ; justifier. La continuité de l'énergie stockée dans la bobine entraîne la continuité de l'intensité. i1(½T) = A1 exp(-T/(2t)) +E/R = A1a+E/R ; i2(½T) = A2 exp(-T/(2t)) -E/R = A2a-E/R i1(½T) =i2(½T) ; A1a+E/R =A2a-E/R ; A2a -A1a =2E/R. En écrivant que le courant est périodique, écrire une seconde relation entre A1 et A2. Résoudre le système. i2(T) =i1(0) : A2 exp(-T/t) -E/R = A1 +E/R ; A2a2= A1 +2E/R. A1 = A2 -2E/(Ra) ; A2a2=A2 -2E/(Ra) + 2E/R ; A2(a2-1) =2E/R(1-1/a) ; A2 = 2E/( a (a+1)R). A1 = A2 -2E/(Ra) = 2E/( a (a+1)R)-2E/(Ra) ; A1 = -2E/((1+a)R). Exprimer i1(t) et i2(t). Tracer le graphe i(t) en faisant apparaître les points remarquables. i1(t) =-2E/((1+a)R) exp(-t/t) +E/R ; i1(t) =E/R [ 1-2/(1+a)exp(-t/t) ]. i2(t) = 2E/( a (a+1)R) exp(-t/t) -E/R ; i2(t) =E/R [ -1+2/(1+a)a)exp(-t/t) ]. On va maintenant étudier l'influence de l'inductance de lissage. 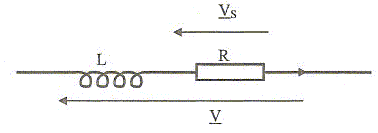Montrer que pour une tension sinusoïdale V de pulsation w, l'ensemble R et L se comporte comme un filtre passe-bas du premier ordre. Pour cela, on calculera en notant V et Vs les grandeurs complexes associées aux tensions, la fonction de transfert H(jw) = Vs /V que l'on exprimera en fonction de w et t. Puis on étudiera le comportement du module H de H(jw) pour les grandes et les petites pulsations. V = (jLw +R) i ; Vs = R i ; Vs /V = R / (jLw +R) = 1 /(jLw/R +1) ; H(jw) = 1/(1+jwt ). H(jw) = (1-jwt ) / ( 1+(wt)2) ; H = 1/( 1+(wt)2)½. si w tend vers zéro, H tend vers 1 ; si w tend vers l'infini, H ~ 1/(wt). Comportement d'un filtre passe-bas du 1er ordre. Déterminer la pulsation de coupure wc du filtre. H(wc) = Hmax / 2½ = 1 /2½ ; ½ = 1/( 1+(wct)2) ; 1+(wct)2) = 2 ; (wct)2 = 1 ; wc = 1/t. La tension en crénaux u(t) admet une décomposition en série de Fourier de la forme : Justifier le fait que seuls les coefficients ßn correspondants à des n impairs soient différents de zéro. La fonction sinus et la tension crénaux sont des fonctions impaires. Calculer les coeficients ß1 et ß3 de la décomposition en série de Fourier de la tension uS(t). Vs(t) = H V(t) = (1-jwt ) V(t) / ( 1+(wt)2) exp(jq) = cos q + j sin q ; -j exp(jq) = -j cos q +sin q ; sin q est la partie réelle de -j exp(jq). à b2k+1sin((2k+1)w0t) on associe la partie réelle du complexe : -jb2k+1 exp(j(2k+1)w0t) ; à ß2k+1sin((2k+1)w0t +Fs 2k+1) on asocie la partie réelle du complexe : -jß2k+1exp(jFs 2k+1 )exp(j(2k+1)w0t) -jß2k+1exp(jFs 2k+1 )exp(j(2k+1)w0t) = -(1-j(2k+1)wt ) jb2k+1 exp(j(2k+1)w0t) /( 1+(2k+1)2(wt)2) ß2k+1exp(jFs 2k+1 ) =(1-j(2k+1)wt ) b2k+1/( 1+(2k+1)2(wt)2) Le nombre complexe a+jb s'écrit r exp(jq) avec r =(a2+b2)½ et tan q = b/a. ici a = b2k+1/( 1+(2k+1)2(wt)2) et b =-(2k+1)wt ) b2k+1/( 1+(2k+1)2(wt)2) Identifier les parties réelles : ß2k+1 = b2k+1/( 1+(2k+1)2(wt)2)½. b2k+1= 4E/((2k+1)p) ; ß2k+1 = b2k+1/( 1+(2k+1)2(wt)2)½. b1 =4E/p ; ß1 = 4E/(p ( 1+(wt)2)½ ; b3 =4E/(3p) ; ß3 = 4E/(3p ( 1+9(wt)2)½. Déterminer le rapport B = ß3/ß1 et le calculer si w = wc. B = ( 1+(wct)2)½ / [3( 1+9(wct)2)½ ]; avec wct = 1 B = 2½/(3*10½) =0,15. Pour alimenter la charge avec un courant quasi-sinusoïdal, on modifie la commande des interrupteurs pour modifier la tension u(t) et obtenir une tension ud(t) représentée ci-dessous : Cette tension admet la décomposition en série de Fourier suivante : Comment faut-il choisir q pour que l'harmonique de rang 3 soit nul ? Dans ce cas, calculer pour la plus petite valeur positive de q et pour w = wc, le rapport D = d5/d1, où d5 est l'amplitude de l'harmonique de rang 5 et d1 est l'amplitude du fondamental ( ou harmonique de rang 1) de la tension aux bornes de R. Conclure. cos (1,5w0q) = cos((2k+1) p /2) ; 1,5w0q=(2k+1) p /2 ; q=(2k+1) p /(3w0). La plus petite valeur de q est : q= p /(3w0) b1 = cos (w0q/2) = cos ( p/6) =0,866 ; b5 = cos (5w0q/2)/5 = cos ( 5p/6) /5= -0,173. D = d5/d1 =| b5 H(5wc)/ (b1 H(wc) ) |; H(5wc) =1/( 1+25(wct)2)½ = 1/26½ =0,196 ; H(wc) =1/( 1+(wct)2)½ = 1/2½ =0,709 ; D =|-0,173*0,196 /(0,866*0,709) |= 0,055. L'harmonique de rang trois a une amplitude nulle ; l'harmonique de rang 5 a une amplitude égale à 5,5 % de l'amplitude du fondamental. La tension us(t) est quasiment sinusoïdale.   Donner dans ces conditions en fonction de E et R, la puissance moyenne sur une période reçue par la charge. La puissance moyenne est voisine de la puissance du fondamental. us(t) = 4E/p b1 sin (w0(t-½q)) H(wc) = 4E/p*0,866 *0,709 sin (w0t-p/6) =0,782 E sin (w0t-p/6). p(t) = u2(t) / R =( 0,782 E)2 sin2 (w0t-p/6) / R ; la valeur moyenne de sin2 est ½) puissance moyenne : (0,782 E)2/(2R) =0,31 E2/R.

retour -menu