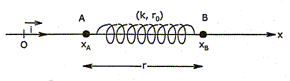|
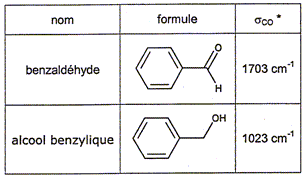
Diodes, modèle harmonique de la liaison de valence concours Capes interne 2009
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
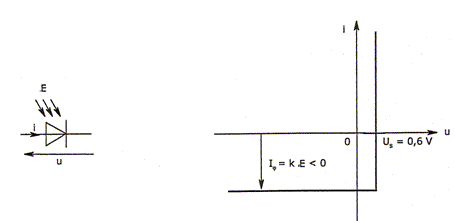
La figure ci-dessous présente une modélisation très simple de la caractéristique courant-tension d'une photodiode pour la convention donnée :
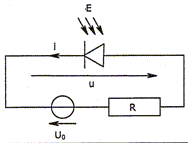
L'intensité notée Ij <0, appelée courant inverse, est proportionnelle à l'éclairement E qui irradie la photodiode. Pour utiliser la photodiode en capteur, on l'alimente de manière à ce qu'elle soit polarisée en inverse ( u<0 et i<0). Le circuit est représenté ci-dessous :
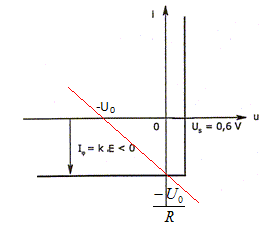
Reproduire sur la copie l'allure de la caractéristique de la diode. Superposer la caractéristique i(u) du générateur de Thévenin ( U0, R) branché aux bornes de la diode de manière à ce que le point de fonctionnement du circuit soit bien dans la zone de polarisation de la diode.
u = -U0-Ri avec i = -kE ; u = -U0+ R k E si u est nulle : -U0+ Rlim k E < 0 ; Rlim < U0 /(kE). Déterminer la valeur numérique de Rlim pour E = 0,20 mW cm-2. On donne k = 50 µA mW-1 cm2 = 5 10-5 A mW-1 cm2 = et U0 = 5,0 V. kE = 5 10-5 * 0,20 = 10-5 A ;
Rlim <5,0 /10-5 ;
Rlim < 5,0
105 ohms.
On étudie un modèle très simple de liaison covalente polaire entre deux atomes A et B : A et B sont assimilables à deux points matériels de masse respective mA et mB liés par un ressort de constatnte de raideur k, de longueur au repos r0. A et B coulissent sur un axe horizontal sans frottement. Ils sont repérés sur cet axe par leur abscisses respectives xA et xB. On note r = xB-xA, la longueur du ressort.
A t=0, on écarte A et B de manière à ce que r = rm, on lâche ensuite les masses sans vitesse initiale. On s'intéresse à l'évolution de r en fonction du temps. Faire le bilan des forces exeercées sur A puis sur B. Le poids des atomes est négligeable devant la force de rappel F = - k ( r-r0) On note r1 : position de A par rapport au centre de masse de la molécule AB et r2 : position de A par rapport au centre de masse de la molécule AB. mA r1 = mB r2 et r1 + r2 = r ; mA r1 = mB ( r - r1) ; r1 = mB r / (mA+mB). (1) En appliquant la relation fondamentale de la dynamique, montrer que l'équation différentielle vérifiée par r peut se mettre sous la forme : r" +W02r = W02 r0. W0 est une constante que l'on exprimera en fonction de mA, mB et k et dont on donnera la dimension. mAd2r1/dt2 = -k(r-r0) ; (1) donne : d2r1/dt2 = mB / (mA+mB) d2r/dt2 ; mAmB / (mA+mB) d2r/dt2= -k(r-r0). On pose µ = mAmB / (mA+mB) , la masse réduite. d2r/dt2=-k / µ (r-r0) ; d2r/dt2 + k/µ r = k/µ r0 avec W02 = k/µ. raideur k : force / longueur ; force = masse fois accélération = masse * longueur / temps2. [k]= M T-2. [µ] = M d'où [k /µ] = T-2 et [(k /µ)½] = T-1. Résoudre l'équation différentielle pour établir l'expression de r en fonction du temps en tenant compte des conditions initiales. Solution générale de r" +W02r =0 ; r(t) = A cos (W0t + j) avec A et j des constantes. solution particulière de r" +W02r = W02 r0 : r = r0. Solution générale de r" +W02r = W02 r0 : r(t) = A cos (W0t + j) + r0. A t = 0 : rm = A cos j + r0. [dr/dt]t=0 =[-AW0 sin (W0t + j)]t=0 =-AW0 sin j = 0 ; par suite j = 0 A = rm - r0. r(t) = (rm - r0) cos (W0t )+ r0. Lorsqu'un rayonnement IR de pulsation w interagit avec une liaison polaire A-B, le ressort modélisant la liaison décrit des oscillations forcées, à la pulsation w, et absorbe pour ce faire, l'énergie du rayonnement lumineux. Lorsque w =W0, l'absorption est maximale et de traduit sur un spectre, par une faible transmittance. Les oscillations observées sont appelées vibrations de valence de la liaison A-B.
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|