Statique des fluides, thermique, chimie, pH, Bts enveloppe du bâtiment 2009 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

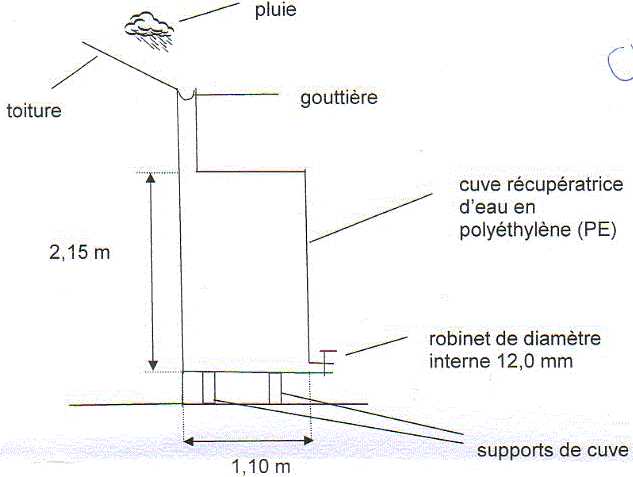
Un particulier décide de placer sous un gouttière du toit de sa maison une cuve récupératrice d'eau de pluie. Cette cuve est en polyéthylène(PE) et a la forme d'un cylindre de diamètre interne 1,10 m et une hauteur interne de 2,15 m. Le robinet de sortie est placé en bas de la cuve. Le diamètre du robinet est de 12,0 mm. Statique des fluides. 7 points On considère que la surface de la toiture utile pour récupérer cette eau de pluie est de 90,0 m2. Une pluie moyenne apporte 3,00 litres par mètre carré de toiture utile par heure. Montrer que l'unité L m-2 h-1 correspond à la dimension d'une vitesse. L est l'unité d'un volume ; m2 est l'unité d'une surface ; L m-2 est l'unité d'un volume divisé par une surface, c'est donc un longueur. Une longueur divisée par des heures correspond bien à une vitesse. Calculer l'eau de pluie que peut contenir la cuve. Volume du cylindre : pi D2/4 h = 3,14 *1,102/4*2,15 =2,04 m2. Pendant combien de temps doit-il pleuvoir pour remplir la cuve en totalité ? 3,00 * 90 = 270 litres = 0,27 m3 par heure de pluie. 2,04 / 0,27 = 7,57 h = 7 h 34 min. On considère que la cuve est remplie sur une hauteur de 1,50 m. Calculer les pressions absolue et relative ( effective) de l'eau au niveau du robinet. p0 = 1,01 105 Pa ; masse volumique de l'eau : r = 1,00 103 kg m-3 ; g=9,81 N/kg. Diférence de hauteur entre la surface et le centre du robinet : h = 1,50- 6 10-3 = 1,494 m pRob-p0= rgh = 103*9,81*1,494 =1,4657 104 = 1,47 104 Pa. pRob=p0+ rgh =1,01 105 + 1,4657 104 =1,1566 105 = 1,16 105 Pa. Lorsque la hauteur d'eau est de 50,0 cm, calculer la pression relative au niveau du robinet. Diférence de hauteur entre la surface et le centre du robinet : h = 0,50- 6 10-3 = 0,494 m pRob-p0= rgh = 103*9,81*0,494 =4,8461 103 = 4,85 103 Pa. Calculer la variation de pression au niveau du robinet lorsque la surface libre de l'eau passe de 1,50 m à 0,500 m. 4,8461 103 - 1,4657 104 =-9,81 103 Pa. (le signe moins indique une diminution de pression). Thermique. 7 points Un jour d'hiver ensolleillé la température de l'eau, à l'intérieur de la cuve, passe de 5°C à 12 °C. Lorsque la cuve contient 2,00 m3 d'eau, calculer la quantité de chaleur que celle-ci emmagasine lorsque la température de l'eau passe de 5°C à 12°C. capacité thermique massique de l'eau c = 4,18 103 J K-1 kg-1. Q = m c (tf-ti) avec m = 2000 kg et tf-ti= 7 °C Q = 2000*4,18 103*7 =5,85 107 J. Calculer la quantité de chaleur perdue Q0 par cette eau liquide si elle passe de 12 °c à 0°C puis Q1 lorsqu'elle passe entièrement de l'état liquide à l'état solide à 0°C. Chaleur latente de fusion de la glace L = 3,33 105 J kg-1 ; Q0 = m c (tf-ti) avec m = 2000 kg et tf-ti= -12 °C Q = 2000*4,18 103*(-12) = -1,00 108 J. Q1 =-L m ; Q1 = 2000*(-3,33 105) = -6,66 108 J. L'épaisseur de la cuve en polyéthylène est ePE = 5,00 mm. Calculer la résistance thermique surfacique de la paroi latérale de la cuve lorsque celle-ci est remplie d'eau. Résistances thermiques superficielles rSi = 1/heau = 2,04 10-4 m2 K W-1 et rSE = 1/hair =0,110 m2 K W-1. Conductivité thermique lPE =0,400 W m-1K-1. R = rSi + ePE / lPE +rSE =2,04 10-4 + 5 10-3 / 0,4 + 0,110 = 0,1227 = 0,123 m2 K W-1. On considère que le flux thermique total au travers de la totalité de la cuve est FT=930 W lorsque l'eau passe de 12°C à 0°C. Calculer le temps nécessaire pour que l'eau passe de 12°C à 0°C en considérant le flux thermique constant. Dans l'hypothèse où l'eau reste liquide : t = Q0/FT=1,00 108 / 930 = 1,08 105 s = 29,9 h. A travers la paroi latérale le flux surfacique est de 98,0 W m-2. Calculer le flux thermique perdu au travers de cette paroi latérale ( il y a de l'eau sur toute la hauteur de la cuve). Surface latérale du cylindre S = pi D h = 3,14*1,10*2,15 = 7,43 m2. Flux = - 98*7,43 = 728 W. Pour diminuer de moitié la perte de flux thermque à travers la paroi latérale, le particulier souhaite disposer autour de la surface latérale de la cuve un isolant. Calculer l'épaisseur e de l'isolant pour satisfaire cette diminution. Conductivité thermique lisolant = 0,0300 W m-1K-1. Nouvelle résistance thermique R' = R + e/li ; e = (R'-R) li . Nouveau flux thermique ( cuve isolée) : 728/2 = 364 W 364 = S(tf-ti) /R' ; R' = 7,43*12/364 =0,2449 m2 K W-1. e =(0,2449-0,1227) *0,03 =3,67 10-3 m = 3,67 mm.   Chimie : 6 points On considère maintenant que l'eau de la cuve est à 25°C Le particulier teste le pH de l'eau de pluie et trouve 6,7. La cuve est en polyéthylène ; Donner la formule du polymère et du monomère éthylène ou éthène. Polymère --[-CH2--CH2-]n-- ; monomère CH2=CH2 ou C2H4. L'eau de pluie est-elle acide, basique ou neutre ? A 25°C, un milieu acide a un pH inférieur à 7. L'eau de pluie est acide. Calculer la concentration des ions oxonium H3O+ et hydroxyde HO- présents dans la cuve. Concentration ion oxonium : 10-pH = 10-6,7 =2,0 10-7 mol/L. Concentration en ion hydroxyde : Ke / 10-pH = 10-14 / 10-6,7 = 10-7,3 = 5,0 10-8 mol/L. Le particulier souhaite fire un complément d'eau de sa piscine de 2,00 m3 à l'aide de l'eau de pluie. le pH de l'eau de la piscine doit être de 7,4. Le particulier dispose de deux correcteurs de pH : le premier nommer pH+ est à base de soude, le second nommé pH- est à base d'acide. Lequel choisir ? Il faut élever le pH de l'eau de pluie de 0,7 unité : on choisit donc la soude ( pH+) Sur la notice des deux produits,il est indiqué : " pour faire varier le pH de 0,1 il faut aouter 0,500 kg pour 50,0m3 d'eau". Calculer la quantité de produit qu'il faut ajouter pour faire paser le pH de 2 m3 de 6,7 à 7,4. 7*0,500 *2/50 = 0,140 kg = 140 g.

retour -menu