Analyse par activation neutronique : Bts chimiste 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

L’analyse par activation neutronique est une technique qui consiste à soumettre l’échantillon à analyser à un flux de neutrons, ce qui conduit à activer un certain nombre d’éléments. Après l’irradiation, les radio-isotopes ainsi créés peuvent être identifiés avec certitude et quantifiés avec précision ; ce qui permet de connaître la nature des éléments initialement présents dans l’échantillon tout en effectuant leur dosage. C’est une méthode d’excellence dans la recherche de traces et d’ultra-traces. Elle s’applique à de très nombreux matériaux (métaux, semi-conducteurs, échantillons archéologiques, biologiques, géologiques…) et également dans l’environnement (dosage des poussières atmosphériques…) et en criminologie (détection de l’arsenic…). C’est une technique analytique souvent non destructive, très sensible (limite de détection inférieure à 10-12 g) et qui permet le dosage simultané multi élémentaire. 1. Source de neutrons. La principale source de neutrons est constituée par des réacteurs nucléaires. Cependant, les sources isotopiques sont un moyen d’irradiation autonome et relativement moins coûteux, qui se prête bien à l’utilisation industrielle pour les dosages rapides et en série de certains éléments. Les neutrons sont alors générés par une source « américium-béryllium ». L’américium 24195Am est un émetteur α. Écrire l’équation de la réaction de désintégration sachant qu’il donne naissance au neptunium Np. 24195Am ---> AZNp + 42He. Conservation de la charge : 95 = Z+2 d'où Z = 93 Conservation du nombre de nucléons : 241 = A +4 d'où A = 237. 24195Am ---> 23793Np + 42He. L’américium est intimement mélangé au béryllium 9. Les particules α émises vont réagir sur le béryllium 9 suivant la réaction : α + 94Be --->AZX + ... n Recopier l’équation de la réaction en la complétant. Identifier l’élément X formé. 42He + 94Be --->AZX + 10n. Conservation de la charge : 2+4 = Z d'où Z = 6 ( élément carbone) Conservation du nombre de nucléons : 4+9 = A +1 d'où A = 12. 42He + 94Be --->126C + 10n. Nature de l’échantillon. L’échantillon est un tensioactif qui contient des impuretés (comme le chlore et le brome). Les films de tensioactifs sont utilisés pour construire des matériaux nano-structurés qui connaissent aujourd’hui un essor considérable en raison de leurs propriétés particulières, propriétés qui dépendent de la composition élémentaire des nano-objets. Il est donc nécessaire de contrôler leur pureté par l’analyse élémentaire. Ce film tensioactif agit sur la tension superficielle de l’eau, comme le font les savons ou les détergents. Il comprend deux parties aux propriétés antagonistes : une partie polaire et une partie comprenant une ou plusieurs chaînes hydrocarbonées. Comment sont représentées schématiquement ces deux parties ? Quelles sont les propriétés antagonistes de ces deux parties ? -------------------O longue chaine carbonée lipophile ; tète hydrophile Irradiation de l’échantillon On s’intéresse ici plus particulièrement à la présence de chlore dans l’échantillon, que l’on soumet à un flux de neutrons issus d’un réacteur nucléaire.  Ecrire l’équation de la réaction nucléaire subie par un noyau de chlore 3717Cl absorbant un neutron. 3717Cl + 10n ---> 3817Cl L’isotope instable du chlore formé dans la réaction précédente est radioactif ß-, de temps de demi-vie (ou période radioactive) T½ = 37 min. Ecrire l’équation de cette désintégration sachant que le noyau formé est de l’argon (Ar). 3817Cl ---> 3818Ar +0-1eeci l. e rend très dangereux pour les yeux Analyse qualitative et quantitative. L’énergie totale libérée lors de cette réaction de désintégration ß- vaut E = 4,91 MeV. A l’aide d’un détecteur semi-conducteur au germanium associé à un amplificateur et un analyseur multicanaux, on obtient le spectre de rayons γ accompagnant cette désintégration. On observe l’émission de photons γ d’énergie E1 = 1,64 MeV et E2 = 2,17 MeV. Le bruit de fond étant très bas, on atteint une excellente limite de détection. On fournit  le schéma de désintégration ß- de l’isotope du chlore 37. 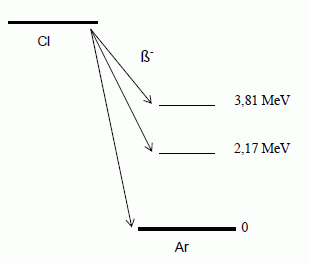  Web www.chimix.com Expliquer quelle est l’origine du rayonnement γ. Le noyau fils d'argon se trouve dans un état excité ; il libère son surplus d'énergie  sous forme de photon gamma, afin de revenir  à un état de moindre énergie.. Les deux énergies des photons γ sont-elles compatibles avec le schéma de désintégration ? Justifier. On observe l’émission de photons γ d’énergie E1 = 1,64 MeV et E2 = 2,17 MeV. L'énergie du noyau est quantifiée : l'énergie des photons gamma doit correspondre  à la différence d'énergie entre deux niveaux d'énergie du noyau. 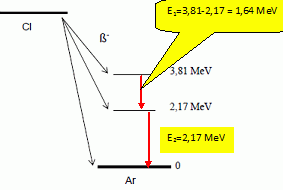 Quand le noyau d’argon est produit dans l’état excité d’énergie E3 = 3,81 MeV, quelle est l’énergie maximale Emax des rayons ß- ? L’énergie totale libérée lors de cette réaction de désintégration ß- vaut E = 4,91 MeV. L'énergie  libérée est la somme des énergies du rayon ß- et du rayon gamma : E = E3 +Emax  ;  Emax   = E - E3 =4,91 -3,81 = 1,10 MeV.  L’activité de l’échantillon, contenant l’isotope Cl instable, au moment du comptage est A = 2,5 x 104 Bq. Sachant que cette activité a été mesurée 37 min après la fin de l’irradiation, quel était l’ordre de grandeur de l’activité à la fin de l’irradiation (c'est-à-dire juste après avoir obtenu le chlore radioactif) ? L’isotope instable du chlore formé  a un de temps de demi-vie (ou période radioactive) T½ = 37 min. Durant une période, l'activité initiale A0 diminue de moitié : A0 = 2 A = 5,0 x 104 Bq. Quel est alors l’ordre de grandeur de la masse de chlore 37 contenu dans l’échantillon ? On donne : la constante d’Avogadro NA = 6 x 1023 mol-1 ; A = λ.N ; ln 2 ≈ 0,7.  l T½ = ln2 avec  T½ = 37 min = 37*60 =2220 s. l = ln2 / T½ =0,7 / 2220 = 3,12 10-4 s-1. A0 = λ.N0 ;  N0 = A0 / λ= 5,0 104 / 3,12 10-4 =1,6 108 noyaux Quantité de matière de chlore 37 : n = N0 / NA =2,7 10-16 mol. Masse molaire du chlore 37 : M = 37 g/mol. masse de chlore 37 dans l'échantillon : m = n M = 2,7 10-16 *37 ~ 10-14 g.

retour -menu