|
La harpe celtique ( bac S Amérique du Nord 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
Données :
Quelles sont les deux fonctions que doit remplir un instrument de musique pour produire un son ? Parmi les différents éléments qui constituent la harpe, quels sont ceux qui assurent ces fonctions ? Instruments de musique : il doit vibrer et émettre. Un excitateur ( corde, anche, membrane frappée...) produit une vibration ; le son est émis grâce à un couplage ( caisse de résonance pour les instruments à cordes, colonne d'air pour les instruments à vent, micro + amplificateur pour les guitatres électroniques) entre l'excitateur et l'air. On considère la corde "la3" de longueur L = 72 cm. Lorsqu'on pince la corde, elle vibre suivant ses différents modes propres de vibration. Représenter l'allure de la corde lorsqu'elle vibre dans le mode fondamental. En déduire, pour
ce mode, la relation entre la longueur L de la
corde et la longueur d'onde l. La distance
séparant deux noeuds consécutifs est
égale à une demi-longueur d'onde :
L =
½l. Etablir la relation liant la fréquence f du fondamental et la célérité v de l'onde sur la corde. f = v / l = v / (½L) = 2 v/L ; v = 2f L. En déduire la valeur de la célérité de l'onde se propageant sur la corde. v = 2 * 440 * 0,72 = 633,6 ~6,3 102 m/s. Quelle devrait être la longueur L1 d'une corde de même nature que la précédente et utilisée dans les mêmes conditions pour émettre le son "la1" ? Une telle longueur est-elle envisageable ? La nature de la corde et les conditions d'utilisation sont identiques : la célérité reste la même. v = 2f L. Si on divise la fréquence par quatre, alors la longueur doit être multipliée par quatre : L1 = 4L = 4*0,72 = 2,88 ~2,9 m. Cette longueur est trop grande pour une harpe. Sur quels paramètres est-il possible d'agir et dans quel sens pour obtenir le son "la1", avec une corde de longueur proche de 72 cm ? v = 2f L. Il faut diviser la célérité par quatre, la fréquence étant 4 fois plus petite. or v = [T/µ]½ : il va falloir augmenter la masse linéique µ ou/et diminuer la tension T de la corde. Si le musicien soulève une palette de l'une des cordes, le son émis par cette corde sera t-il plus grave ou plus aigu ? Justifier. " En soulevant les palettes, on racourcit de quelques centimètres la longueur de chaque corde" La nature de la corde et la tension de la corde sont inchangées : donc la célérité reste la même. v = 2f L. Si la longueur diminue, la fréquence va augmenter : le son sera plus aigu.
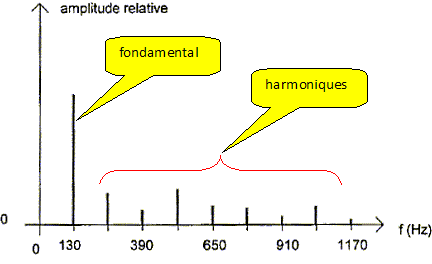
Le musicien joue un "do2". On analyse le son émis et on obtient le spectre suivant. Quelle est la hauteur du son émis ? A quoi correspondent les différentes fréquences obtenues ? Par quelle(s) relation(s) sont-elles liées ? La hauteur du son est la fréquence du fondamental. soit f = 130 Hz. les fréquences des harmoniques sont des multiples de la fréquence du fondamental.
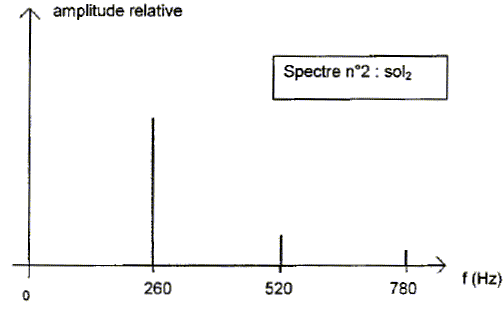
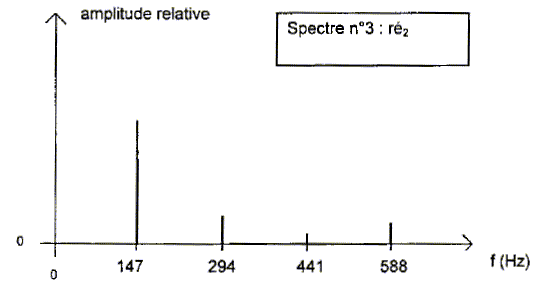
Lorsque le musicien joue deux notes simultanément, l'effet produit à l'oreille dépend de l'intervalle entre les deux notes jouées. On appelle intervalles consonants ou consonances, les intervalles agréables à l'oreille, et intervalles dissonants ou dissonances, ceux pour lesquels l'impression est plus ou moins désagréable. L'effet de consonance peut s'expliquer par le recouvrement plus ou moins important des harmoniques de chacune d'elles, autrement dit, les deux notes doivent avoir des harmoniques en commun.
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||