Etude d'une solution d'hydroxylammonium ( bac S Polynésie 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . .

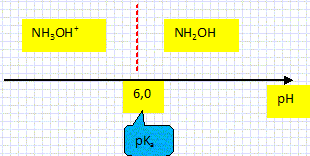
Le chlorure d'hydroxylammonium de formule NH3OHCl est un solide ionique blanc qui, industriellement, est utilisé dans la synthèse de colorants et de produits pharmaceutiques. Il est très soluble dans l'eau. On se propose d'étudier le caractère acide d'une solution aqueuse S de chlorure d'hydroxylammonium préparée au laboratoire. On donne : pKa ( NH3OH+aq / NH2OH aq) = 6,0 à 25°C. Ecrire l'équation de dissolution du chlorure d'hydroxylammonium dans l'eau. NH3OHCl (s) = NH3OH+aq + Cl-aq. Donner la définition d'un acide selon Bronsted. Espèce, ion ou molécule susceptible de céder un proton H+. Ecrire l'équation (1) de la réaction entre l'ion hydroxylammonium et l'eau. NH3OH+aq + H2O(l) = NH2OH aq + H3O+aq. (1) Déterminer le domaine de prédominance de chaque espèce du couple. Dosage de la solution S. 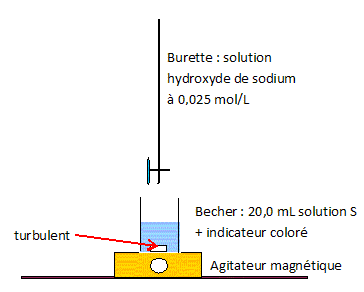On dose un volume VA = 20,0 mL de la solution S par une solution aqueuse d'hydroxyde de sodium Na+aq + HO-aq de concentration molaire en soluté apporté cB= 2,5 10-2 mol/L. On repère l'équivalence à l'aide d'un indicateur coloré acido-basique. Faire un schéma annoté du montage nécessaire à ce dosage. Ecrire l'équation (2) de la réaction de dosage entre les ions hydroxylammonium et les ions hydroxyle. NH3OH+aq + HO-aq = NH2OH aq +H2O(l) (2)   Web www.chimix.com Définir l'équivalence. A l'équivalence les quantités de matière de réactifs mis en présence sont en proportions stoechiométriques ; avant l'équivalence l'un des réactif est en excès, après l'équivalence, l'autre réactif est en excès. Le pH du mélange à l'équivalence vaut 9,1. Choisir l'indicateur coloré dans la liste suivante et préciser le changement de couleur à l'équivalence. teinte de la forme acide teinte de la forme basique zone de virage hélianthine rouge jaune 3,1 - 4,4 rouge de méthyle rouge jaune 4,2 - 6,2 phénolphtaléine incolore rose 8,2 - 10,0 La zone de virage de l'indicateur coloré doit contenir le pH du point équivalent : la phénolphtaléine convient. Dans le becher, avant l'équivalence, l'acide est en excès ( solution incolore) ; après l'équivalence, la soude est en excès et le pH est supérieur à 9,1, donc teinte rose. Le virage de l'indicateur coloré est obtenu pour un volume versé de la solution aqueuse d'hydroxyde de sodium Véq = 24,0 mL. Calculer CA. Quantité de matière d 'acide : CA VA ; quantité de matière de base : CB Véq ; à l'équivalence CA VA = CB Véq. CA = CB Véq / VA = 0,025 * 24,0 / 20,0 = 0,030 mol/L. Le pH de la solution aqueuse S est 3,8. En déduire la concentration des ions oxonium dans cette solution. [H3O+] = 10-pH = 10-3,8 1,585 10-4 ~ 1,6 10-4 mol/L. Etablir le tableau d'avancement de la réaction (1). avancement (mol) NH3OH+aq + H2O(l) = NH2OH aq + H3O+aq initial 0 n0 solvant 0 0 état final réel xf n0-xf large excès xf xf état final si réaction totale xmax n0-xmax xmax xmax Donner l'expression du taux d'avancement final t en fonction de n0 et nf( H3O+) puis en fonction des concentrations molaires CA et [ H3O+].Calculer sa valeur. Cette réaction est-elle totale ? t = nf( H3O+) / n0. nf( H3O+) = [H3O]f V avec V volume de la solution. n0 = CA V ; t =[H3O]f / CA. t =1,6 10-4 / 3,0 10-2 = 5,3 10-3. t est inférieur à 1 : la réaction de l'ion hydroxylammonium avec l'eau est limitée ; elle n'est pas totale. En déduire la constante d'acidité Ka de la réaction (1) puis la calculer. Ka = [NH2OH aq]éq [H3O+aq]éq / [NH3OH+aq]éq [NH2OH aq]éq =[H3O+aq]éq = xf /V avec V : volume de la solution. [NH2OH aq]éq =[H3O+aq]éq = 1,6 10-4 mol/L. [NH3OH+aq]éq =(n0-xf) / V = CA - [H3O+aq]éq =0,030 - 1,6 10-4= 2,984 10-2 mol/L. Ka = (1,585 10-4)2 / 2,984 10-2 = 8,4 10-7. En déduire la valeur du pKa puis la comparer avec celle donnée. pKa = - log ( 8,4 10-7) = 6,07 ~ 6,1. écart relatif : ( 6,1-6) *100/ 6 = 1,7 %. La valeur trouvée et la valeur donnée sont identiques à 1,7 % près.

retour -menu