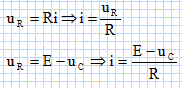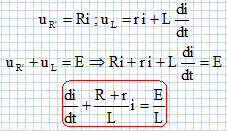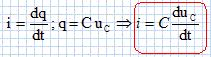Etude expérimentale de dipôles électriques ( bac S Polynésie 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . .

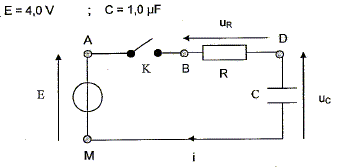
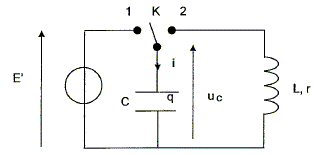
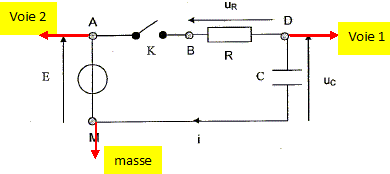
Dipôle résistance et condensateur en série. On réalise le circuit représenté ci-dessous, constitué d'un générateur idéal de tension continue de force électromotrice E, d'un interrupteur K, d'un conducteur ohmique de résistance R et d'un condensateur de capacité C. On utilise une interface d'acquisition pour observer les tensions uC et E en fonction du temps. A quels points A, B, D ou M du circuit doit-on relier les voies 1 et 2 et la masse de l'interface pour visualiser uC sur la voie 1 et E sur la voie 2 ? Pour visualiser uC= uDM, on relie le point D à la voie 1 et M à la masse. Pour visualiser E= uAM, on relie le point A à la voie 2 et M à la masse. 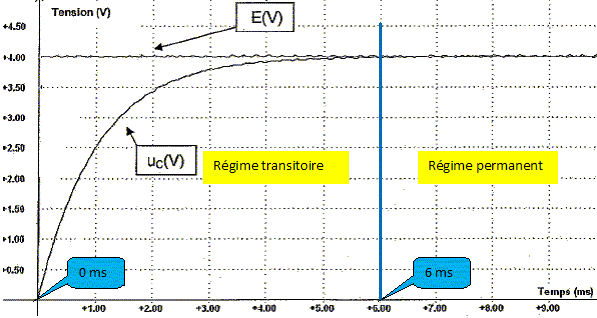A t=0, on déclenche l'acquisition en fermant l'interrupteur K. Les courbes uC(t) et E= f(t) sont données. Qualifier les deux régimes de fonctionnement du circuit en choisissant parmi les adjectifs suivants : périodique, permanent, pseudo-périodique, transitoire. Préciser les dates limitant chacun des régimes. Quel phénomène physique se produit pendant le premier régime ? 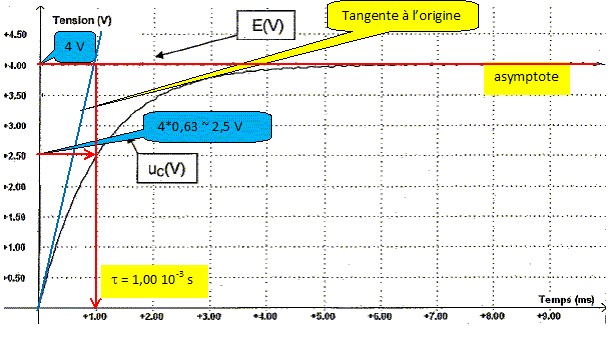Pendant le régime transitoire, le condensateur se charge : la tension uC croît de 0 à E. Déterminer graphiquement la valeur de la constante de temps t en expliquant la méthode utilisée. Donner l'expression littérale de t et en déduire la valeur dela résistance R. t = RC ; R = t / C = 1,00 10-3 / 1,0 10-6 = 1,0 103 ohms. En appliquant la loi d'additivité des tensions, donner la relation liant E, uR et uC. uR + uC = E. Exprimer uR en fonction de i et en déduire une expression littérale de l'intensité du courant i en fonction de E, uC et R. Calculer i pour t1=0 et t2 = 9 ms. date (ms) uC (V) i (A) 0 0 4,0 10-3 9 4,0 0 Représenter, sans considération d'échelle , l'allure de la courbe i =f(t).   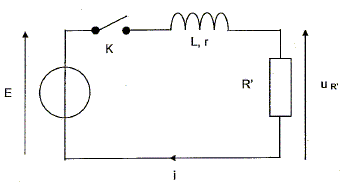Web www.chimix.com Dipôle résistance et bobine série. Le circuit étudié est constitué d'une bobine de résistance r et d'inductance L, d'un générateur idéal de tension de force électromotrice E, d'un interrupteur K et d'un conducteur ohmique de résistance R'. E = 4,0 V ; L = 11 mH , R' = 10 ohms. 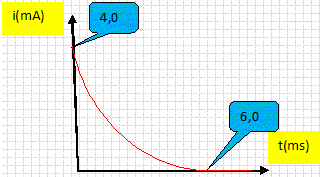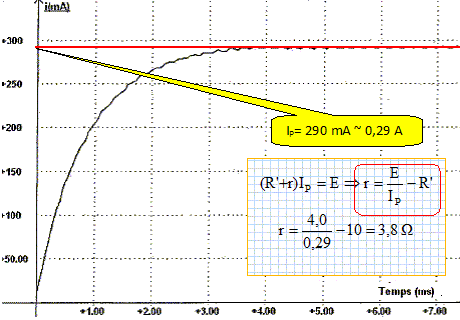A partir de la fermeture de l'interrupteur K, on observe la tension uR à l'aide d'une interface d'acquisition reliée à un ordinateur. Quel est l'intérêt de faire le relevé de cette tension uR' ? La tension uR' aux bornes d'un conducteur ohmique et l'intensité i qui le traverse sont proportionnelles : l'image de uR' est celle de l'intensité au facteur R' près. i(t) = uR'(t) / R' = uR'(t) /10 avec uR'(t) en volt et i(t) en ampère. Le tableur du logiciel d'acquisition nous permet de calculer les valeurs de i et de tracer la courbe i(t). Quel est le phénomène physique mis en évidence dans ce cas ? Quel élément du circuit est la cause de ce phénomène ? La bobine d'inductance L introduit un retard à l'établissement du courant i. En appliquant la loi d'additivité des tensions, déterminer l'équation différentielle vérifiée par l'intensité i. En régime permanent, i vaut alors IP. Que devient l'équation différentielle ? L'intensité étant constante en régime permanent, la dérivée de l'intensité par rapport au temps est nulle : dIP/dt = 0. L'équation différentielle s'écrit : (R'+r) IP= E. En déduire l'expression littérale de la résistance r de la bobine puis déterminer sa valeur. Dipôle bobine et condensateur en série. Quel est le phénomène physique se produisant lorssque l'interrupteur est placé en position 1 ? Est-il lent ou instantané ? Justifier. K en position 1 : le condensateur se charge. La résistance R du circuit de charge est très faible ( celle des fils électriques) ; la constante de temps du circuit de charge vaut t = RC ; t est donc très faible. La durée de la charge étant voisine de 5 t, la charge est quasiment instantanée. On bascule alors l'interrupteur en position 2 et, à partir de cet instant choisi comme origine des dates, on relève la tension uC en fonction du temps à l'aide de l'interface d'acquisition reliée à un ordinateur. On obtient le graphe suivant. En puisant dans le vocabulaire suivant, décrire le phénomène qui se produit dans le circuit : apériodique, annulation, électrique, forcée, mécanique, libre, non amortie, installation, amortie, oscillation. Oscillation électrique libre amortie. On souhaite suivre l'évolution énergétique du circuitRLC en fonction du temps. Il faut calculer à l'aide d'un tableur, l'énergie électrique Ee accumulée dans le condensateur et l'énergie magnétique Em accumulée dans la bobine. Donner les expressions littérales de Ee et Em. Ee = ½u2C/C ; Em = ½Li2. En respectant les conventions du schéma, exprimer i en fonction de la dérivée de uC par rapport au temps. 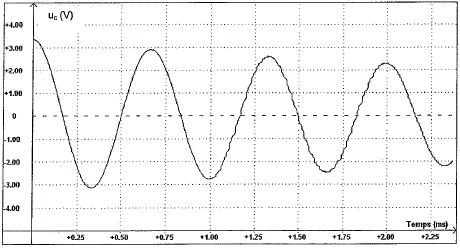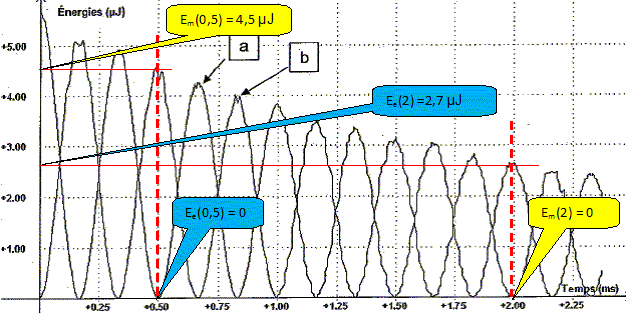Les courbes Ee(t) et Em(t) sont données : En justifiant attribuer les grandeurs Ee ou Em aux courbes a et b. A la date t = 0, la charge du condensateur est maximale et l'intensité du courant i est nulle : le condensateur stocke alors toute l'énergie du dipôle RLC tandis que la bobine ne stocke pas d'énergie. Courbe a : Ee(t) ; courbe b : Em(t). Donner les valeurs des deux énergie Ee et Em aux dates t1 = 0,5 ms et t2 = 2,0 ms. Comparer les variations simultanées des énergies emmagasinées par le condensateur et la bobine entre ces deux dates. Condensateur : Ee(2)-Ee(0,5) = 2,7-0 = 2,7 µJ Bobine : Em(2)-Em(0,5) = 0-4,5 = -4,5 µJ Em(2)-Em(0,5) est, en valeur absolue, supérieure à Ee(2)-Ee(0,5). Comment évolue l'énergie totale du circuit entre les instants de dates t1 et t2 ? A quoi cette évolution est-elle due ? L'énergie totale du circuit diminue : lors des échanges d'énergie entre condensateur et bobine, une partie de l'énergie est dissipée sous forme de chaleur ( effet Joule) dans les parties résistives du circuit.

retour -menu