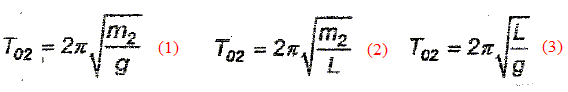Sur une balançoire : chute libre, corrosion et protection du fer ( bac S Nlle calédonie mars 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

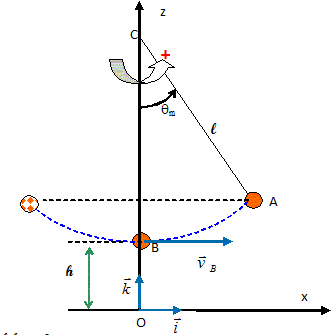
Deux enfants, Pierre (10 ans) et Sophie (7 ans) font de la balançoire dans un square. Pour simplifier l'étude mécanique, le système S1 {Sophie sur le siège, balançoire} peut être modélisé par un pendule simple de longueur L et de masse m1. De même, le système S2 {Pierre sur le siège, balançoire} peut être modélisé par un pendule simple de longueur L et de masse m2 > m1. Toute l'étude mécanique est effectuée dans le référentiel terrestre considéré comme galiléen. Données : L = 1,80 m ; distance sol-extrémité du pendule à l'équilibre : h = 0,50 m ; intensité de la pesanteur : g = 9,8 N.kg-1. Oscillations libres. Cette première partie permet de savoir si l'affirmation suivante de Pierre est correcte : " Je suis plus lourd que toi, je me balancerai donc plus rapidement ". Cette affirmation peut être traduite en langage scientifique par : " la période de mes oscillations sera plus courte ". Dans le cas d'oscillations de faibles amplitudes l'expression de la période propre des oscillations du système S2 est l'une des trois proposées ci-dessous : En procédant à une analyse dimensionnelle, proposer la seule possible. pi est sans dimension, T est un temps, donc l'expression sous le radical doit être homogène à un temps au carré. (1) m est une masse ; g est une accélération, une longueur divisée par un temps au carré ; [m/g] = M L-1T2. [m/g]½ = M½ L-½T, non homogène à un temps. (2) m est une masse ; L est une longueur ; [m/L] = M L-1. [m/L]½ = M½ L-½, non homogène à un temps. (3): L est une longueur ; g est une accélération, une longueur divisée par un temps au carré ; [L/g] = L L-1T2. [L/g]½ = T, homogène à un temps. En déduire si l'affirmation de Pierre est correcte ou non. L'affirmation est incorrecte : la période est indépendante de la masse.  Sophie, assise sur la balançoire, est lâchée à la date t0 = 0, sans vitesse initiale, d'un point A d'abscisse angulaire qA =qm = 50°. En considérant qu'il n'y a pas de frottements choisir, en justifiant parmi les quatre courbes suivantes, celle qui correspond à l'évolution temporelle de l'abscisse angulaire q du système S1 en fonction du temps. 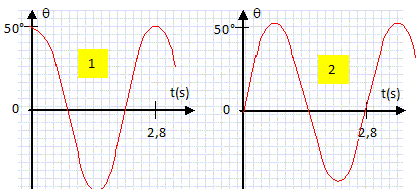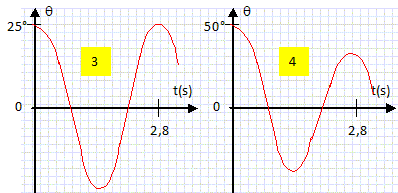(1) : à t = 0, l'angle q vaut 50° et il n'y a pas d'amortissement. (2) : à t = 0, l'angle q vaut 0° ( ne convient pas). (3) : à t = 0, l'angle q vaut 25° ( ne convient pas). (4) : amortissement important ( ne convient pas). Mesurer alors la valeur de la période propre T01 du système. 2,8 s. 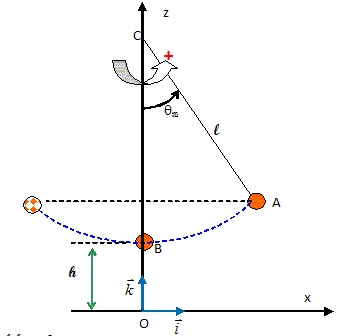Chutes libres. Lors des oscillations, Sophie procède à une expérience en lâchant une bille de métal pendant le mouvement de façon à ce qu'elle touche le sol loin du point O. Pierre dit : " pour que la bille aille loin du portique, tu dois la lâcher lorsque tu arrives tout en haut ". Sophie répond : " non, la bille ira encore plus loin si je la lâche du point le plus bas car c'est là qu'elle va le plus vite ". Dans toute la suite de l'exercice, on considère que la bille est assimilable à un point matériel de masse m = 30 g, que la position initiale de la bille avant la chute est confondue avec l'extrémité du pendule simple et que le mouvement s'effectue sans frottement. Quelle est la valeur de vA, vitesse de la bille au point A, si l'on considère que Sophie lâche la bille sans lui donner d'impulsion ? Au point le plus haut, l'énergie mécanique du système {bille}est entièrement sous forme potentielle de pesanteur : vA=0. Quelle est la nature du mouvement de la bille après avoir été lâchée du point A ? La bille n'est soumise qu'à son poids : il s'agit d'une chute libre verticale sans vitesse initiale. Déterminer l'abscisse x1 de la bille lorsqu'elle atteint le sol. x1 est égale à l'abscisse du point A : x1 = L sin qm = 1,80 sin 50 = 1,38 m. On étudie maintenant le cas où la bille est lâchée du point B. Au cours du mouvement, l'énergie potentielle de pesanteur de la bille est maximale au point A et vaut EPA = 0,34 J. L'origine des énergies potentielles est choisie à l'altitude du point O tel que z = 0. En appliquant la loi de conservation de l'énergie mécanique entre A et B, donner l'expression littérale de la vitesse vB de la bille et montrer que sa valeur est vB = 3,6 m.s-1. En A, l'énergie mécanique est entièrement sous forme potentielle de pesanteur ; En B, l'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle de pesanteur : ½mvB2 + mgh. Seul le poids travaille entre A et B : l'énergie mécanique se conserve : ½mvB2 + mgh = 0,34 vB = [2(0,34/m -gh)]½ = [ 2(0,34/0,03 -9,81*0,5)]½ =3,6 m/s. On a représenté ci-dessous sans souci d'échelle le vecteur vitesse de la bille, lors du second passage de Sophie par la verticale. Donner les valeurs des coordonnées vBx et vBz du vecteur vitesse. vBx = 3,6 m/s ; vBz= 0 m/s. En utilisant la seconde lui de Newton, donner les coordonnées ax et az du vecteur accélération de la bille au cours de sa chute. La bille n'est soumise qu'à son poids, d'où : ax =0 ; az = -g = -9,81 m s-2. Établir les équations horaires x(t) et z(t) en prenant pour origine des dates l'instant de passage au point B dans le sens indiqué sur la figure. Le vecteur vitesse est une primitive de l'accélération : vx = 3,6 : vy = -gt = -9,81 t. Le vecteur position est une primitive du vecteur vitesse : x = vBxt + xB = vBxt = 3,6 t (1) y = -½gt2 +yB = -½gt2 + h = -4,9 t2 + 0,5.(2) Equation de la trajectoire de la bille : (1) donne t = x/vBx ; repport dans (2) : y = -½g x2/v2Bx +h y = -4,9 /3,62 x2+0,5 =-0,378 x2+0,5 Donner l'expression littérale de l'abscisse x2 de la bille lorsqu'elle atteint le sol et calculer sa valeur. Au sol y=0 : -½g x2/v2Bx +h =0 ; x2 = 2 hv2Bx /g ; x = vBx [2h/g]½ =3,6[2*0,5 /9,81]½ =1,15 m. Comparer x1 et x2 et dire si Sophie a raison dans ce cas d'étude. x2 < x1, Sophie a tord. Corrosion et protection du fer : Dans cette partie, on s'intéresse à la corrosion du fer constituant le portique. Pour comprendre ce phénomène, on réalise au laboratoire les expériences suivantes. A. Mise en évidence de la corrosion du fer. On considère le dispositif expérimental suivant : Dans le compartiment 1, on fait barboter un courant de diazote afin de désoxygéner la solution ; dans le compartiment 2, on fait barboter du dioxygène. Après une dizaine de minutes, on arrête les ajouts de gaz et on introduit dans chaque compartiment un gros clou en fer. On relie les deux clous en série avec un conducteur ohmique et un ampèremètre utilisé en continu. L'ampèremètre indique une valeur positive. En déduire le sens du courant puis les signes respectifs des bornes de la pile ainsi fabriquée. Dans cette pile, quel est le rôle de la laine de verre imbibée de chlorure de potassium ? Elle joue le rôle d'un pont salin ( assure entre autre la continuité électrique) et évite le mélange des solutions contenues dans chaque branche. Les couples oxydant-réducteur intervenant dans le fonctionnement de la pile sont : Fe2+ (aq) / Fe (s) et O2(aq) / H2O (l ). Quelle est l'espèce réduite lors du fonctionnement de cette pile ? A la cathode positive, l'oxydant, le dioxygène est réduit. Écrire la demi-équation électronique traduisant cette réduction. O2(aq) + 4 e- +4H+(aq) = 2 H2O ( l). ou encore O2(aq) + 4 e- +2 H2O ( l)= 4HO-(aq) . Comment nomme-t-on l'électrode à laquelle a lieu la réduction ? Cathode. On observe à l'autre électrode une oxydation du fer. Écrire la demi-équation électronique traduisant cette oxydation. Fe (s) = Fe2+ (aq) + 2 e-. On considère un morceau de fer (extrémité du portique) enfoncé en partie dans le sol. Prévoir si le métal fer sera oxydé plutôt dans le sol (zone moins aérée) ou dans l'air. Dans l'expérience ci-dessus, le fer est oxydé dans le compartiment de gauche, le moins riche en dioxygène. Le fer sera donc plutôt oxydé dans le sol. 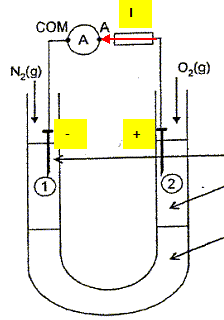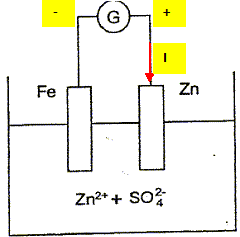Protection du fer. Pour empêcher l'oxydation du fer dans le portique, celui-ci est recouvert d'une couche de zinc métallique. Dans l'industrie, on utilise pour cela diverses techniques en fonction du type de pièces métalliques à protéger. Une de ces techniques est l'électrozingage dont un schéma simplifié est proposé ci-dessous. G représente un générateur de tension continue. Les lames de fer et de zinc plongent dans une solution aqueuse de sulfate de zinc. Préciser le sens du courant dans la partie métallique du circuit et les signes des bornes du générateur sachant que la lame de fer se recouvre de zinc métallique. Justifier. Les ions zinc Zn2+(aq) se réduisent à la cathode négative. Zn2+(aq) + 2e- = Zn(s). Le métal zinc recouvre le fer.

retour -menu