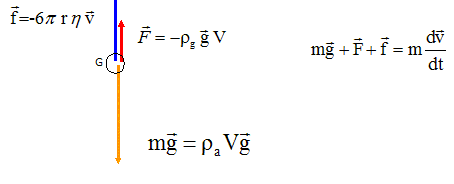Chute d'une bille dans un fluide visqueux ( bac S Inde 2009). En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

Une éprouvette contenant un liquide visqueux sert de support à l'étude de la chute d'une bille d'acier. Le schéma ci-dessous, qui donne une idée du montage, n'est qu'indicatif. En particulier, il ne respecte pas d'échelle et ne peut pas servir de support pour des mesures. Les vecteurs sont écrits en gras et en bleu. La bille, qui constitue le système étudié, est lâchée sans vitesse initiale à l'instant t 0. Au même instant, une acquisition vidéo assurée par une webcam couplée à un ordinateur est déclenchée de manière à enregistrer 25 images par seconde. La position instantanée x du centre G de la bille est repérée par l'axe vertical orienté vers le bas Ox, de vecteur unitaire i . A t =0, G est en G0. Le vecteur-vitesse de G est noté v = v. i . La vidéo est ensuite analysée à l'aide d'un logiciel approprié qui permet de repérer aux dates t i les positions successives x i de G lors de son mouvement descendant et de calculer approximativement la vitesse moyenne v i entre les dates t i -1 et t i + 1. La détermination des vitesses v i aux instants t i donne l'enregistrement suivant : Expliquer comment le logiciel permet de déterminer les vitesses v i à partir des positions x i aux instants t i. 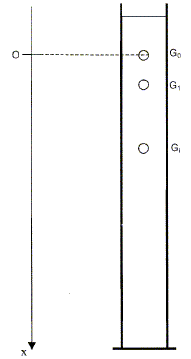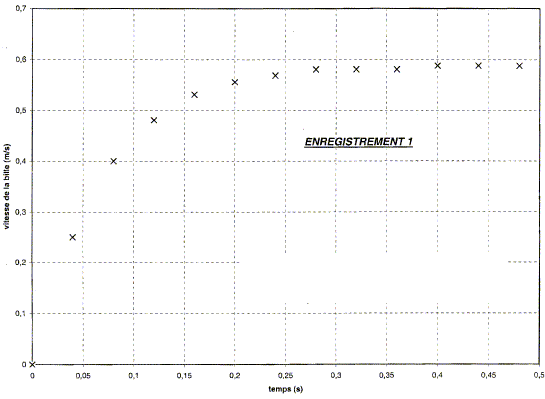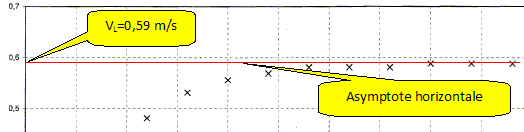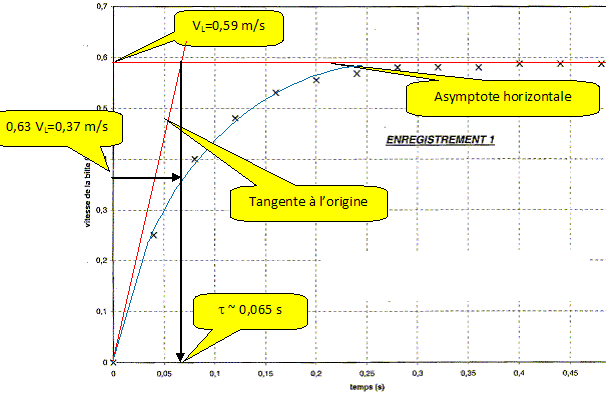Calcul de la vitesse moyenne sur une durée aussi petite que possible ( deux fois la durée séparant deux images consécutives) v i = ( x i +1 - x i - 1 ) / ( t i +1 - t i - 1) Mettre en évidence l'existence d'une vitesse limite VL dont on donnera la valeur. Equation du mouvement. On considère comme système la bille plongée dans le liquide et en mouvement par rapport à celui-ci. Faire le bilan des forces qui s'exercent sur le système. Les représenter sur un schéma. La bille est soumise à son poids, à la poussée d'Archimède et à une force de frottement fluide. On note m et V la masse et le volume de la bille, ra et rg les masses volumiques respectives de l'acier qui constitue la bille et du liquide dans laquelle celle-ci est plongée. g= g i est l'accélération de la pesanteur. On suppose que la force (" résistance" ) exercée par le fluide sur la bille en mouvement est de la forme F= -k v, k étant une constante positive. Déterminer l'équation différentielle vérifiée par la fonction v(t). Montrer qu'elle est de la forme : dv/dt = -k/m v + ag. Ecrire la seconde loi de Newton suivant l'axe vertical descendant : mg - rg V g - k v = m dv/dt avec m = ra V soit V = m / ra mg - m rg/ ra g - k v = m dv/dt mg( 1-rg / ra) - k v = m dv/dt dv/dt = -k/m v +g( 1-rg / ra) ; on pose a = ( 1-rg / ra) Vérifier que la fonction v(t) = a g m/k [ 1-exp(-k/m t)] est solution de l'équation précédente et vérifie la condition initiale à t =0, v =0. dv/dt = a g exp(-k/m t), repport dans l'équation différentielle : a g exp(-k/m t) =- a g [ 1-exp(-k/m t)] + ag. a g exp(-k/m t) =- a g +a g exp(-k/m t)+ ag. Cette égalité est vérifiée quelque soit le temps. La fonction proposée est bien solution de l'équation différentielle. v(t) = a g m/k [ 1-exp(0)] = a g m/k [ 1-1] = 0. On prend dorénavant les valeurs suivantes, données dans le système international SI : m =5,00.10-3 kg ; g = 9,81 m.s-2·; k = 7,60.10-2 kg.s-1 ; a= 0,906. Dans l'équation différentielle ou dans l'expression de la solution, mettre en évidence l'existence d'une vitesse limite. Calculer sa valeur et la comparer à celle trouvée ci-dessus. exp(-k/m t) tend vers zéro au bout d'un temps très grand : la vitesse tend vers VL= a g m/k . VL= 0,906*9,81*5,00.10-3 / 7,60.10-2 =0,585 m/s, valeur en accord avec celle trouvée graphiquement. Utiliser l'analyse dimensionnelle pour déterminer l'unité de m/k . m : masse ; [m]= M k est une force divisée par une vitesse ; une force est une masse fois une accélération ; une accélération est une longueur divisée par un temps au carré. [k ] = M T-1. [m/k] = T. Calculer numériquement ce rapport. m/k = 5,00.10-3 / 7,60.10-2 =6,58 10-2 s. Quelle interprétation peut-on donner de cette grandeur ? m/k est la constante de temps du système : au bout d'une durée voisine de 5 m/k, la vitesse limite est pratiquement atteinte. Par une méthode de votre choix et que vous expliciterez, déterminez sur l'enregistrement la valeur du temps t caractéristique du phénomène. Conclusion. On retrouve la valeur calculée ci-dessus.

retour -menu