|
Détection d'exoplanètes ( bac S France 2009). En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
Avec les instruments actuels, da détection directe des exoplanètes n'est guère possible. En effet d'après Michel mayor, un des grand spécialistes du sujet, observer une exoplanète reviendrait à essayer de distinguer à 1000 km une flamme de bougie près d'un phare. Différents moyens sont employés pour deviner l'existence de ces planètes si éloignées de nous. En décembre 2006, le satellite Corot, équipé d'un tlescope et de différents instruments de mesure, a été mis en orbite avec pour objectif la détection et l'étude de nouvelles exoplanètes. En mai 2007, un communiqué de presse anonce le succès des premières observations de Corot : une nouvelle exoplanète a été découverte. Les résultats à venir sont très attendus par les scientifiques aussi bien que par le grand public. D'après Sciences magazine et Internet. La première partie de cet exercice montre que la présence d'une exoplanète ne peut pa être détectée par un télescope classique. La seconde partie montre que l'on peut détecter une exoplanète en observant ses passages périodiques devant son étoile. Observations au télescope. A la lecture de différents articles scientifiques, Julie et Léa, deux jeunes astronomes amateurs, décident d'observer avec leur télescope une exoplanète et son étoile. Grâce à une base de données d'exoplanètes disponible sur Internet, elles choisissent le couple HD 209458 situé dans la constellation de Pégasse. Julie et léa pointent leur télescope dans la direction souhaitée et après vérification des réglages,observent l'étoile mais pas sa compagne... Analysons le problème sans tenir compte de la luminosité de l'étoile par rapport à l'exoplanète. Un extrait de la fiche technique du
télescope utilisé pour les observations est
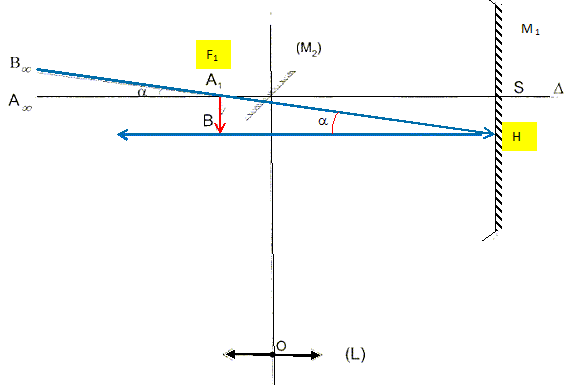
donnée ci-dessous : M2 le miroir secondaire plan incliné de 45 ° par rapport à D ; L : oculaire assimilable à une lentille convergente de foyers F2 et F'2 et d'axe optique D'. Le couple exoplanète - étoile, situé à l'infini est noté AB et son diamètre apparent a. L'image de AB donnée par le miroir primaire M1 est notée A1B1. Indiquer en justifiant, la position du foyer F1 sur la figure. L'image d'un objet AB situé à l'infini se forme dans le plan focal image du miroir primaire. F1 est donc confondu avec A1.
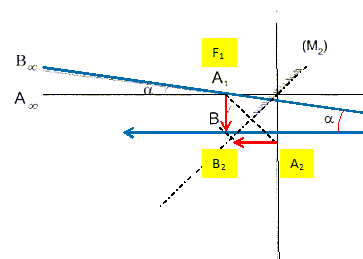
Exprimer a en fonction de f1 et A1B1. Dans le triangle A1B1H : tan a =A1B1/ f1. Si l'angle a est petit on peut confondre sa tangente avec l'angle exprimé en radian. a ~A1B1/ f1. On note A2B2 l'image donnée par le miroir plan de A1B1. Indiquer la position de A2B2. Quelle relation existe t-il entre les longueurs A1B1 et A2B2. A1B1 et A2B2 sont symétriques par rapport au plan du miroir M2. Du fait de cette symétrie, A1B1 est égale à A2B2.
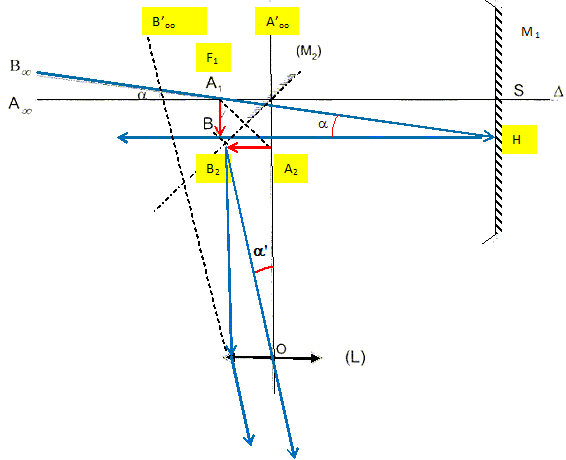
Le réglage du télescope étant afocal, l'image A2B2 se forme dans le plan focal objet de l'oculaire. On appelle A'B' l'image de l'objet A2B2 donnée par l'oculaire. Où se forme l'image définitive A'B' du couple exoplanète-étoile ? A2B2 se forme dans le plan focal objet de l'oculaire : donc l'image définitive se forme à l'infini. Justifier la réponse précédente après avoir fait un tracé de deux rayons lumineux caractéristiques issus de B2, traversant l'oculaire L.
Faire figurer le diamètre apparent a' sous lequel est vu le couple étoile- exoplanète à travers le télescope. Exprimer a' en fonction de A2B2 et f2. Dans le triangle A2B2O : tan a' =A2B2/ f2. Si l'angle a est petit on peut confondre sa tangente avec l'angle exprimé en radian. a' ~A2B2/ f2 = A1B1/ f2 Le grossissement Gr d'un instrument d'optique est défini par la relation Gr = a' /a. Montrer que Gr = f1 / f2 et calculer la valeur de ce rapport. a' =A2B2/ f2 =A1B1/ f2 ; a=A1B1/ f1 ; d'où Gr = a'/a =f1 /f2 =1200 / 30 = 40.
On considère que deux points sont aisément discernables à l'oeil nu s'ils sont observés sous un diamètre apparent supérieur ou égal à 3,5 10-4 rad. Caractéristiques du couple
étoile-exoplanète : Estimer la valeur du diamètre apparent a sous lequel est vu le couple étoile-exoplanète à l'oeil nu. a = dimension du couple observé / distance observateur- couple exoplanète - étoile. dimension du couple observé = 0,045 u.a = 0,045*150 109 =6,75 109 m distance observateur- couple exoplanète - étoile =9,5 1015 * 153 = 1,45 1018 m a =6,75 109 / 1,45 1018 =4,7 10-9 rad. Estimer la valeur du diamètre apparent a' sous lequel est vu le couple étoile-exoplanète à travers le télescope. a' = 40 a =40*4,7 10-9 = 1,9 10-7 rad. On considère que deux points sont aisément discernables à l'oeil nu s'ils sont observés sous un diamètre apparent supérieur ou égal à 3,5 10-4 rad. L'étoile et l'exoplanète ne sont pas discernables même à travers le télescope.
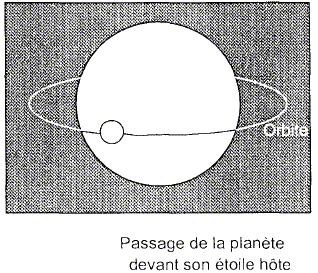
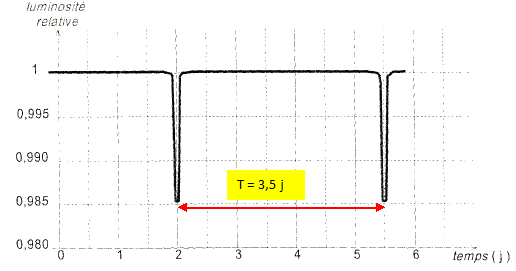
Méthode des transits. La méthode des transits utilise un photomètre placé à la sortie du télescope ; cet instrument permet de mesurer la luminosité de l'astre observé. Le passage répété d'une planète devant son étoile provoque une diminution périodique de la luminosité de son étoile.
La mesure de la luminosité de l'étoile HD 209458 en fonction du temps conduit au graphe suivant :
|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|