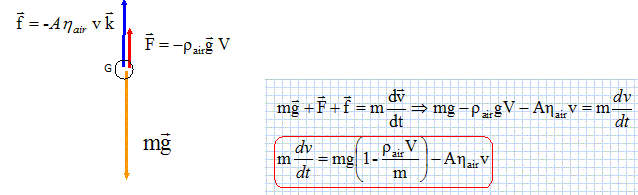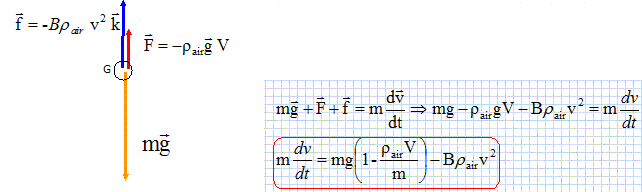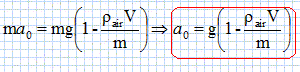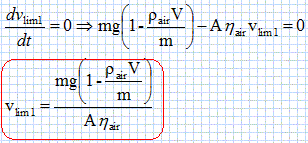Frottements avec l'air : qu'en dit la NASA( bac S France 2009). En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

Les vecteurs sont écrits en gras et en bleu. Intrigué par la notion de frottement fluide introduite en classe, un élève recherche des informations sur la notion de force de trainée. Sur le site de la NASA dont l'activité se partage entre domaine spatial et aéronautisme, l'élève trouve : " La force de traïnée sur un avion ou sur une navette dépend de la densité de l'air, du carré de la vitesse, de la viscosité et de la compressibilité de l'air, de la forme et de la taille de l'objet ainsi que de son inclinaison par rapport à l'écoulement d'air. En général la dépendance à l'égard de la forme du corps , de l'inclinaison, de la viscosité et de la compressibilité de l'air sont très complexe ". D'après www.NASA.gov. A l'issue de cette recherche, l'élève dégage deux modèles pour rendre compte des frottements exercés par l'air sur les objets. - Modèle 1 : les frottements dépendent, entre autre, de la viscosité de l'air hair et de la valeur de la vitesse du centre d'inertie G du système. On exprime alors la force sous la forme : f = -A hair v k où A est une constante. - Modèle 2 : les frottements dépendent, entre autres, de la masse volumique de l'air rair et du carré de la vitesse v. On exprime alors la force sous la forme : f = -B rair v2 k où B est une constante. Les constantes A et B sont liées à la forme du corps et à son inclinaison. Le choix entre les deux modèmes est lié à l'expérience. Son professeur lui conseille de les appliquer à la chute verticale d'une grappe de ballons de baudruche dont il peut lui fournir le film. Il lui donne également les valeurs approchées de A et B. Un logiciel adapté permet d'obtenir la courbe d'évolution temporelle de la valeur v de la vitesse de centre d'inertie G du système. Le système fourni par l'ensemble des ballons de baudruche, de masse m et de volume total V, est lâché sans vitesse initiale dans le champ de pesanteur g uniforme et vertical. Toute l'étude est faîte dans le référentiel terrestre supposé galiléen. On donne : A ~1 x101 m ; B~2 x10-2 m2 ; m = 22 g ; g = 9,8 m s-2 ; rair =1,2 kg m-3 = 1,2 g/L ; hair = 2 10-5 kg m-1 s-1. Rappeler ce que signifie le caractère uniforme du champ de pesanteur. La direction, le sens et la valeur ( norme) du champ de pesanteur g sont constants. Le système est soumis à trois forces, son poids P, les frottements f et la poussée d'Archimède F. Donner les caractéristiques de la poussée d'Archimède L. Verticale, vers le haut, norme égale au poids du volume d'air déplacé (F = rair g V), appliquée au centre d'inertie du système. Si on choisit le modèle 1, montrer que dans que dans le référentiel terrestre ( supposé galiléen), la vitesse v vérifie l'équation différentielle : m dv/dt = mg [ 1 -rair V/ m]- Ahair v De la même façon montrer que pour le modèle 2 on obtient l'équation suivante : m dv/dt = mg [ 1 -rair V/ m]- Brair v2.   Web www.chimix.com Accélération initiale. Déduire des équations différentielles l'expression littérale de a0, valeur de l'accélération à la date t=0 en fonction de m, V, g et rair. 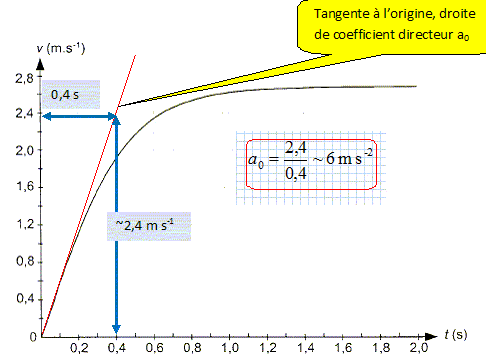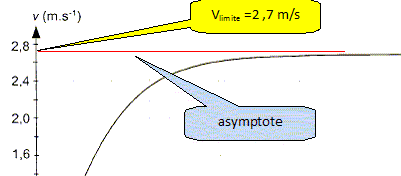La vitesse initiale est nulle. Vérifier par une méthode graphique que a0 est de l'ordre de 6 m s-2. Retrouver cette valeur par un calcul si V ~ 7 L. g = 9,8 m s-2 ; rair =1,2 kg m-3 = 1,2 g/L ; m = 22 g ; rair V/m = 1,2*7 / 22 =0,38. a0 = 9,8 ( 1-0,38) = 6 m s-2. Vitesse limite. Déterminer graphiquement la valeur de la vitesse limite.   A l'aide de l'équation différentielle, démontrer dans le cas du modèle 1 que l'expression de cette vitesse limite est : v lim 1= mg [ 1 -rair V/ m] /( Ahair) Calculer la valeur approchée de vlim 1. 1-rair V/m = 1-0,38 = 0,62 ; A hair = 10* 2 10-5 = 2 10-4 ; vlim 1 = 0,022*9,8 *0,62 / 2 10-4 = 6,7 102 ~ 7 102 m/s. Sachant que vlim 2 est proche de 2 m/s, comparer ces deux vitesses limites avec la valeur trouvée expérimentalement. En déduire quel modèle est le plus adapté. Le modèle 2 est le plus adapté car il conduit à une vitesse limite proche de la valeur expérimentale. Force de frottement et énergie. Le travail de la force de frottement est dissipé sous forme de chaleur ; le bouclier thermique des navettes spatiales est destiné à les protéger lors de leur entrée dans l'atmosphère. Pour l'expliquer sur un forum, l'élève a rédigé le texte suivant : " La navette pèse 70 tonnes ; elle quitte une orbite basse ( 250 km) autour de la Terre et se déplace à environ 28 000 km/h par rapport à la Terre lorsqu'elle amorce sa descente. Le plus problèmatique avant l'atterrissage n'est pas de descendre de 250 km,mais de ralentir afin que sa vitesse soit d'environ 400 km /h. Pour cela il faut dissiper 2 térajoules en 2000 secondes, soit 1 mégawatt moyen ! Actuellement cette énergie est dissipée sous forme de chaleur lors du frottement de la Navette avec l'air de l'atmosphère : l'énergie cinétique de la navette diminue,la navette ralentit et se réchauffe ". Citer les noms des formes dénergie que possède la navette en orbite autour de la Terre. Energie cinétique et énergie potentielle de pesanteur. Dans la phrase :"...il faut dissiper 2 térajoules en 2000 secondes, soit 1 mégawatt moyen .." donner le nom des deux grandeurs physiques dont les valeurs numériques sont soulignées. 2 térajoules : valeur d'une énergie ; 1 mégawatt : valeur d'une puissance. En ne prenant en compte que la variation de vitesse, calculer la valeur des deux grandeurs citées à parir des données fournies dans le texte. Vos résultatys sont-ils en accord avec ceux de l'élève ? 1 térajoule = 1TJ = 1012 J. Enegie cinétique initiale : ½mv2 avec v = 28 000 /3,6 = 7,8 103 m/s ; m = 7,0 104 kg. ½mv2 = 0,5 * 7,0 104 (7,8 103)2 = 2,1 1012 J = 2,1 TJ. Enegie cinétique finale : ½mv2 avec v = 400 /3,6 = 1,1 102 m/s ; m = 7,0 104 kg. ½mv2 = 0,5 * 7,0 104 (1,1 102)2 = 4,3 108 J. La variation d'énergie cinétique est de l'ordre de -2 TJ. ( en accord) Puissance dissipée(W) : énergie(J) divisée par la durée(s) = -2 1012 / 2000 = -1 109 W = -1000 MW ( en désaccord avec le calcul de l'élève)

retour -menu