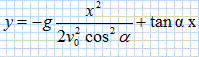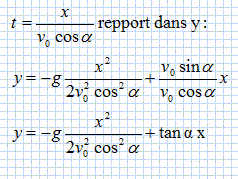Un tobogan de plage ( bac S Antilles 2009) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

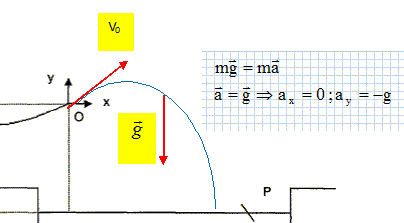
Un enfant glisse sur un tobogan de plage dans le référentiel terrestre supposé galiléen. Pour l'exercice l'enfant sera assimilé à un point matériel G et on négligera tout type de frottement ainsi que toutes les actions dues à l'air. Les vecteurs sont écrits en gras et en bleu. Un tobogan de plage est constitué par : - une piste DO qui permet à l'enfant partant de D sans vitesse initiale d'atteindre le point O avec un vecteur vitesse v0 faisant un angle a avec l'horizontale. - une piscine de réception : la surface de l'eau se trouve à une distance H au dessous de O. -On donne : masse m de l'enfant m = 35 kg ; g = 10 m s-2 ; h = 5,0 m ; H = 0,50 m ; a = 30 °. On choisit le point O comme référence pour l'énergie potentielle de pesanteur. Mouvement de l'enfant entre D et O. Donner l'expression de l'énergie potentielle de pesanteur Epp D au point D. Epp D = m g h. Donner l'expression de l'énergie mécanique Em D au point D. L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique. Or la vitesse initiale en D est nulle : l'énergie cinétique en D est donc nulle. Par suite : Em D =Epp D = m g h. En déduire la réaction globale de fonctionnement de la pile. Donner l'expression de l'énergie mécanique Em O au point O. L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique. Or l'énergie potentielle de pesanteur est nulle en O ( référence). Par suite : Em O =Ec O = ½m v20. En déduire l'expression de la vitesse en O en justifiant. En absence de frottement, seul le poids travaille et l'énergie mécanique se conserve : Em O = Em D = ½m v20 = mgh. v20 = 2gh ; v0 = [2gh]½. Calculer la valeur de la vitesse de l'enfant en O. v0 = [2*10*5,0]½ =10 m /s. En réalité la vitesse en ce point n'est que de 5,0 m/s. Comment justifier cette différence ? Les frottements sur le support et sur les couches d'air ne sont pas négligeables et l'énergie mécanique diminue au cours de la glissade sur le tobogan. Etude de la chute de l'enfant dans l'eau. En O, origine du mouvement dans cette partie, on prendra v0 = 5,0 m/s. Enoncer la deuxième loi de Newton. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées au système étudié, est égale au produit de la masse du système par l'accélération du centre d'inertie du système. Appliquer la seconde loi de Newton à l'enfant lorsqu'il a quitté le point O. Déterminer l'expression des composantes ax et ay du vecteur accélération dans le repère Oxy. L'enfant n'est soumis qu' à son poids : la chute est dite " libre". Déterminer l'expression des composantes vx et vy du vecteur vitesse dans le repère Oxy. Le vecteur vitesse est une primitive de l'accélération. vx = constante ; la constante est égale à la vitesse initiale projetée sur l'axe des x. vx = v0 cos a. vy = -gt constante ; la constante est égale à la vitesse initiale projetée sur l'axe des y. vy = -gt + v0 sin a. Déterminer l'expression des composantes x et y du vecteur position dans le repère Oxy. Le vecteur position est une primitive du vecteur vitesse. L'enfant étant à l'origine du repère à la date t = 0, les constantes d'intégration seront nulles. x = v0 cos a t. y = -½gt2 + v0 sin at.     Montrer que l'expression de la trajectoire de l'enfant, notér y'x) a pour expression : En déduire la valeur de l'abscisse xP du point d'impact P de l'enfant dans l'eau. y = -10 x2 / (2*25 *cos230) + x tan 30. y = -10 x2 / (2*25 *cos230) + x tan 30. y = -0,2667 x2 + 0,577 x. Au point P, y = -H = -0,50 m -0,50 = -0,2667 x2 + 0,577 x. 0,2667 x2 - 0,577 x -0,50 = 0 x2 -2,16 x -1,875 =0 discriminant D = 2,162+4*1,875 = 12,17 ; D ½=3,49 x1 = ½(2,16 -3,49) , valeur négative à ne pas retenir xP = ½(2,16+3,49)= 2,8 m.

retour -menu