Composition des mouvements : vitesse, accélération

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

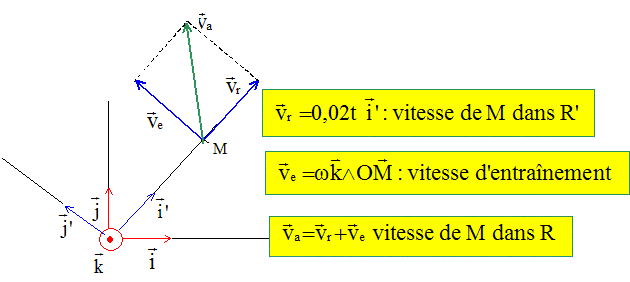
Les vecteurs sont écrits en gras et en bleu.

Déterminer les vitesses relative, d'entrainement et absolue du point marériel.

Référentiel fixe, absolu, R muni du repère orthonormé (O, i, j, k).

Référentiel mobile, relatif, R' muni du repère orthonormé (O, i', j', k).

wk : rotation de R' par rapport à R.

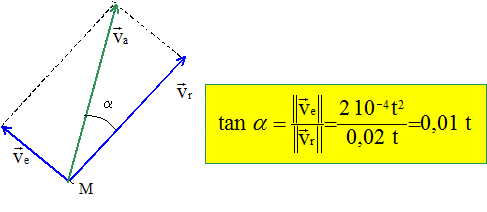
Abscisse de M dans R' : OM= x =½at² = 0,01 t².

Norme de la vitesse relative : v_r=at = 0,01 t.

Norme de la vitesse d'entraînement : v_e = w x = 0,02*0,01 t² = 2 10^-4 t².

Déterminer la norme et la direction du vecteur vitesse absolue.

Norme de la vitesse absolue : v_a= [v_e² + v_r²]^½ =[4 10^-8 t⁴ + 10^-4 t² ]^½ = 0,01 t [4 10^-4 t²+1]^½.

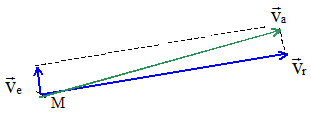
Calculer les coordonnés du poimt M à la date t= 2 s et dessiner les 3 vecteurs vitesses.

Dans le référentiel R' : x= ½at² = 0,01 t² ; y = z = 0.

x(t=2 ) = 0,04 m = 4 cm ; y=0 ; z=0.

La droite OA a tourné de : q= wt = 0,02*2 = 0,04 rad.

vr(t=2)=0,02 m/s = 2 cm/s. ve (t=2)= 8 10-4 m/s = 0,08 cm/s. va (t=2)=[4 +6,4 10-3]½ = 2,0 cm/s ; tan a = 0,02 rad.

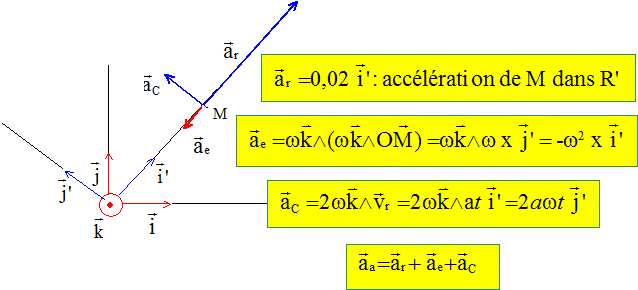
a_r : accélération relative ; a_e: accélération d'entraînement ; a_C: accélération de Coriolis ; a_a: accélération absolue.

Calculer la norme et la direction du vecteur accéleration absolue du point M.

a_r= 0,02 m s^-2 ; a_e= -w²x avec x = ½at² ; a_e= -½w² at² ; a_C=2wa_r t ;

a_a = [(a_r-a_e)² + a_C²]^½ =[(0,02-½w² at² )² +(2wa_r t)²]^½.

Dessiner ces 3vecteurs à la date t=2 s.

a_r= 0,02 m s^-2 ; a_e= -½w² at² = -1,6 10^-5 m s^-2 ; a_C=1,6 10^-3 m s^-2.