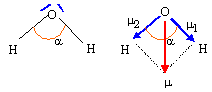L'eau : moment dipolaire, conductivité, piles concours Mines 07 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

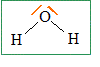
Etude structurale du solvant. Donner la configuration électronique, dans l'état fondamental, des atomes de la molécule d'eau. En déduire la représentation de Lewis de la molécule d'eau. H : 1s1 ; O : 1s2 2s2 2p4. Déduire, à partir de la theorie V.S.E.P.R., la géométrie de l'arrangement des doublets électroniques dans la molécule d'eau et la géometrie de cette derniere. 2 doublets liants et deux doublets non liants autour de l'atome central, l'oxygène. Type AX2E2, en forme de V. Justifier la valeur numérique de l'angle a entre les liaisons O-H. Ces 4 paires se disposent autour de l'atome central, de telle manière que les répulsions soient minimales. La molécule d'eau à la forme d'un V : l'angle est inférieur à 109 ° 28 , la répulsion entre les doublets non liants étant plus importante que la répulsion entre les doublets liants. Le module du moment dipolaire permanent de la molécule d'eau vaut 1,85 D. Déterminer le moment dipolaire (sens et norme) des liaisons O-H en debye et en C.m. Pourcentage du caractère ionique de la liaison OH : dO-H = 96 pm m1 = m2 ; m = 2 m1 cos (½a) ; m1 =m / ( 2cos (½a)) = 1,85 / (2*cos (104,5 / 2 )) = 1,52 D. or 1 Debye = 1D = 3,33 10-30 C m d'où m1 =1,52* 3,33 10-30 = 5,06 10-30 C m Calculer le pourcentage ionique des liaisons O-H. Conclure. Pourcentage de caractère ionique : m1 /( e dOH) = 5,06 10-30 / (1,6 10-19 * 96 10-12) = 0,329 ( 33 %).   La liaison O-H a un caractère polaire très marqué. Conductivité de l'eau pure.  L’eau pure est le siège d’une réaction d’autoprotolyse. Écrire l’équation de cette réaction. Calculer à 25°C la conductivité théorique de l’eau pure. 2H2O = HO-(aq) + H3O+(aq). Conductivité molaire ionique lHO- =2,0 10-2 S m2 mol-1 ; lH3O+ =3,5 10-2 S m2 mol-1. conductivité s(S m-1) =lHO- [HO-] +lH3O+[H3O+] avec [HO-] =[H3O+] = 10-7 mol/L = 10-4 mol m-3. s=3,5+2,0) 10-2*10-4 = 5,5 10-6 S m-1. Au laboratoire, la mesure de la conductivite de l'eau distillée à 25�°C, donne 150 mS.m-1. Commenter cette valeur.   La valeur mesurée est environ 30 fois supérieure à la conductivité de l'eau pure. La présence d'autres ions est responsable de cette valeur : le dioxyde de carbone dissout conduit la formation d'ion hydrogénocarbonate. On cherche à déterminer la valeur du pKe de l’eau pure, supposée inconnue. On construit pour cela deux piles : Pile 1 : Pt |H2(g)|H+(aq) +Cl-(aq)|AgCl(s)|Ag(s) PH2 = 1 bar ; concentration en acide chlorhydrique c = 10-3 mol/L. Pile 2 : Ag(s) |AgCl(s)|(K+(aq) +HO-(aq))+(K+(aq) +Cl-(aq))|H2(g)|Pt PH2 = 1 bar ; concentration en hydroxyde de potassium = concentration en chlorure de potasium c = 10-3 mol/L. Le chlorure d’argent est très peu soluble dans la solution avec laquelle il est en contact. Quelles sont les demi-équations rédox envisageables à chacune des électrodes de la pile 1 ? A l'anode négative en platine, oxydation de H2 : H2 =2H+ 2e-. A la cathode positive en argent, réduction de AgCl(s) : AgCl(s) +e- = Ag(s) + Cl-. Donner l’expression du potentiel de chaque électrode en fonction de C et de constantes thermodynamiques connues. E- = E°(H+ /H2 ) + 0,03 log (C2/PH2) = E°(H+ /H2 ) + 0,03 log C2= E°(H+ /H2 ) + 0,06 log C. E+ = E°(AgCl(s)/ Cl- ) + 0,06 log (1/C). Indiquer le pôle positif de la pile 1 et donner l’expression de la force électromotrice (f.e.m.) E1 de la pile 1 en fonction de C et de constantes thermodynamiques connues. L'argent constitue la borne positive. E1 = E+ -E-=E°(AgCl(s)/ Cl- ) + 0,06 log (1/C) - E°(H+ /H2 ) - 0,06 log C. E1 =E°(AgCl(s)/ Cl- )- E°(H+ /H2 )+0,03 log (1/C2)- 0,03 log C. E1 =E°(AgCl(s)/ Cl- )- E°(H+ /H2 )-0,12 log C. Quelles sont les demi-équations rédox envisageables à chacune des électrodes de la pile 2 ? A l'anode négative en platine, oxydation de H2 en milieu basique : H2+ 2HO- =2e- + 2H2O. A la cathode positive en argent, réduction de AgCl(s): AgCl(s) +e- = Cl- = Ag(s). Donner l’expression du potentiel de chaque électrode en fonction de C, de constantes thermodynamiques connues et de pKe. E- = E°(H+ /H2 ) + 0,03 log (1/([HO-]2PH2))= E°(H+ /H2 ) + 0,03 log (Ke/C)2=E°(H+ /H2 ) + 0,06 log (Ke/C). E+ = E°(AgCl(s)/ Cl- ) + 0,06 log (1/C). Indiquer le pôle positif de la pile 2 et donner l’expression de la force électromotrice (f.e.m.) E2 de la pile 2 en fonction de C, de constantes thermodynamiques connues et de pKe. L'argent constitue la borne positive. E2 = E+ -(-E-)=E°(AgCl(s)/ Cl- ) + 0,06 log (1/C) - E°(H+ /H2 ) - 0,06 log (Ke/C). E2 =E°(AgCl(s)/ Cl- )- E°(H+ /H2 )-0,06 log Ke = E°(AgCl(s)/ Cl- )- E°(H+ /H2 )+0,06pKe. E2=E°(AgCl(s)/ Cl- )- E°(H+ /H2 )+0,06pKe. Les piles sont reliées par leurs électrodes d’argent. La mesure de la force électromotrice de la pile double donne E = 0,472 V à 25°C ; en déduire la valeur du pKe de l’eau à cette température et comparer à la valeur connue à 25°C. E = E2-E1=0,06pKe+0,12 log C. 0,06pKe=E-0,12 log C ; pKe=(E-0,12 log C )/0,06 = (0,472-0,12*(-3))/0,06 =13,87. En prenant 0,059, valeur plus précise, à la place de 0,06 on trouve : pKe=14. La valeur expérimentale est égale à la valeur théorique.

retour -menu