Pyromètre optique : Descartes, lentilles concours Mines 07 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

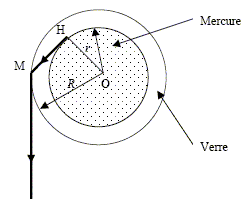
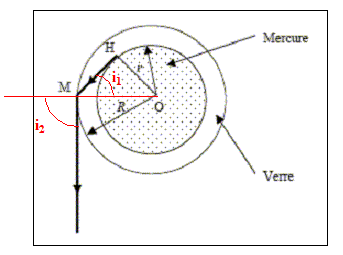
On considère un thermomètre à colonne de mercure, l’enveloppe est un cylindre en verre de rayon extérieur R et de rayon intérieur. Montrer qu’à partir d’une certaine valeur de r/R, un observateur voit le mercure comme s’il remplissait entièrement un cylindre de rayon R, c'est-à-dire que l’épaisseur du verre n’est plus visible. On pourra utiliser les points O, M et H. Loi de Descartes, réfraction en M : nverre sin i1 = nair sin i2 avec nair = 1 et nverre = 1,5. De plus sin i1 = OH/OM= r/R ; sin i2 = nverre r/R nverre r/R inférieur ou égal à 1 soit r/R inférieur ou égal à 1/nverre= 1/1,5 = 0,67. En M, il faut être à la limite de la réflexion totale : r/R inférieur ou égal à 0,67.  Pour mesurer à distance la température TS d’une source, on utilise un pyromètre optique à disparition de filament (gamme de mesure : 700 – 5000 °C). Le principe consiste à comparer l’exitance de l’image de la source avec l’exitance d’un filament préalablement étalonné, la mesure de l’intensité du courant électrique traversant le filament permet d’accéder à la température. L’exitance est la puissance totale émise par rayonnement par unité de surface. Si le filament apparaît en plus clair ou en plus sombre que l’image de la source, sa température est supérieure ou inférieure à TS. Lorsque le filament disparaît, les températures sont identiques. 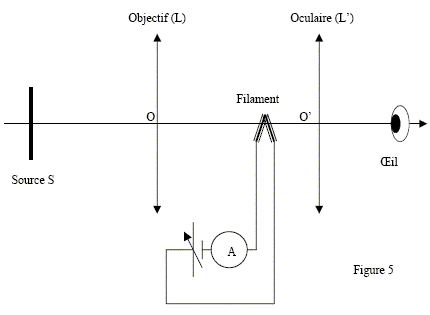Proposer une unité pour l’exitance. " L’exitance est la puissance totale émise par rayonnement par unité de surface" donc W m-2. Sachant que la distance focale de l’objectif (L) est f' =10 cm et que le filament se trouve à une distance d=15 cm de l’objectif, déterminer la position de la source en calculant la distance D=SO. Appliquer la formule de conjugaison à l'objectif L : 1/f' = 1/d - 1/(-D) avec 1/f' = 1/0,1 = 10 d ; d = 0,15 m. 1/D = 1/f'-1/d = 10-1/0,15 = 3,33 soit D= 1/3,33=0,3 m = 30 cm.   L’oculaire (L’) a une vergence v= 5 d. à quelle distance OO' faut-il placer cette lentille pour observer l’image de la source et le filament confortablement ? L'oeil observe sans fatigue à l'infini. L'image définitive doit donc se située à l'infini ; l'image intermédiaire de la source et le filament doivent donc être dans le plan focal objet de l'oculaire L'. Appliquer la formule de conjugaison à l'oculaire : on note A1B1, l'image intermédiaire et A'B' l'image définitive. Les distances algébriques sont écrites en gras et en bleu. 5 = 1/O'A' - 1/O'A1 avec 1/O'A' = 0 ( image à l'infini ) d'où O'A1 = -1/5 = -0,2 m. OO' = O A1+A1O' = 0,15 +0,2 = 0,35 m = 35 cm.

retour -menu