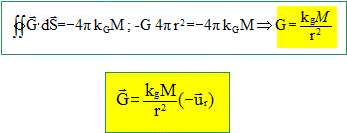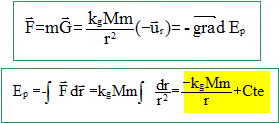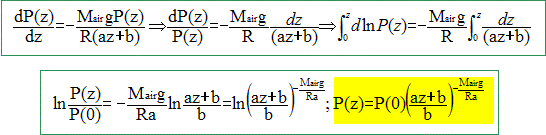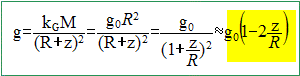vitesse de libération d'une molécule de l'atmosphère terrestre ; température et pression dans la troposphère concours Mines 07 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Définir la température cinétique. La température cinétique d'un gaz parfait est le "reflet "de l'énergie cinétique moyenne des particules. On la définit comme une mesure de l'énergie cinétique moyenne par degré de liberté. ½m<v2>=1,5 kBT On rappelle que la vitesse quadratique moyenne d’une particule est u'=[3kBT/m]½, où kB représente la constante de Boltzmann, m, la masse de la particule et T la température. kB=1,38 10-23 J K-1. Calculer les vitesses quadratiques des molécules de dioxygène et de diazote à une température de 20 °C. O2 : m = 0,032 / 6,02 1023 = 5,32 10-26 kg ; T= 273+20=293 K. u'=[3*1,38 10-23*293/ 5,32 10-26 )]½ =478 m/s. N2 : m = 0,028 / 6,02 1023 = 4,65 10-26 kg ; T= 273+20=293 K. u'=[3*1,38 10-23*293/ 4,65 10-26 )]½ =511 m/s. Les vecteurs sont écrits en gras et en bleu. 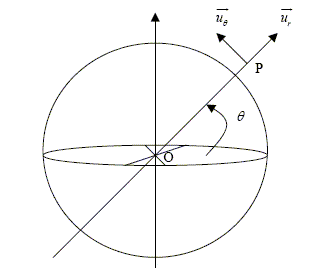L’atmosphère terrestre étant principalement constituée de dioxygène et de diazote, nous allons dans la partie suivante rechercher la vitesse de libération, c'est-à-dire la vitesse nécessaire pour qu’une molécule s’échappe de l’atmosphère terrestre, pour la comparer à la vitesse quadratique moyenne. Le modèle utilisé est celui d’un problème à deux corps : la Terre de masse M de centre O et une molécule de masse m de position P. L’interaction gravitationnelle est la seule prise en compte. L’étude sera conduite dans le référentiel géocentrique muni d’une base orthonormée polaire(ur, uq).   Que peut-on dire de la masse réduite du mobile fictif associé à ce système à deux corps (Terre, molécule) ? Est-ce légitime de supposer le centre de la Terre (supposée sphérique) confondu avec le barycentre du système ? On considérera, dans la suite, la Terre immobile et la particule soumise uniquement au champ gravitationnel terrestre. masse réduite : m= mM/(M+m) Or la masse M de la terre est très supérieure à la masse d'une molécule, en conséquence m proche de m.   En appliquant le théorème de Gauss, déterminer l’expression du champ gravitationnel G à l’extérieur de la Terre à une distance r=OP avec r>RT ; on exprimera G en fonction de r, kG, (constante de gravitation), M et ur. On choisit comme surface de Gauss, une sphère centrée en O et de rayon r >RT. Exprimer la force qui s’exerce sur la particule de masse et en déduire l’énergie potentielle associée à une constante près. Donner une valeur à cette constante en justifiant votre choix. Origine de l'énergie potentielle : l'énergie potentielle est nulle à l'infini, en conséquence la constante d'intégration est nulle. A partir de quelle valeur de l’énergie mécanique la particule est-elle « libre » ? La particule est "libre" lorsque l'énergie mécanique est nulle. En déduire l’expression de la vitesse de libération en fonction de r, kG et M. L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique. EM=½mv2-kGMm/r=0 ; v =[2kGM/r]½. Evaluer cette valeur à la surface de la Terre. r= rayon terrestre = 6,4 103 km = 6,4 106 m ; kG= 6,67 10-11 SI ; M= 6 1024 kg. v = [2* 6,67 10-11 * 6 1024 / 6,4 106 ]½ =11 km/s. Comparer la vitesse de libération aux vitesses quadratiques du dioxygène et du diazote. Conclure. La vitesse de libération est environ 20 fois supérieure aux vitesses quadratiques des molécules : les molécules constituant l'air ne peuvent pas s'échapper de l'atmosphère. Température et pression dans la troposphère. Pour la troposphère, située entre les altitudes 0 et 11 km au-dessus de la Terre, la température est une fonction affine de l’altitude, soit la relation suivante : T(z) = az + b. avec z l’altitude en kilomètres, T la température en kelvin, a et b des constantes. Sachant qu’au niveau du sol la température est de 15°C et de -50°C à une altitude de 10 km , déterminer les coefficients et b en précisant leur unité. T(0) = b = 273+15 ; b= 288 K. T(10) = 10a+288 = 273-50 = 223 ; a = (223-288)/10 ; a = -6,5 K km-1. En assimilant l’air à un gaz parfait de masse volumique µ(z) et de masse molaire Mair, exprimer la masse volumique en fonction de Mair , R(constante des gaz parfaits),z , a, b et P(z)(pression à l’altitude z ). Pour une mole d'air : P(z) V = RT avec V = Mair/m(z) et T= az+b. P(z)Mair/m(z) = R(az+b) ; m(z) = P(z)Mair/(R(az+b)).  En supposant le fluide en équilibre, appliquer le principe de la statique des fluides puis déterminer la pression en un point de la troposphère en fonction de z, a, b, Mair, R, g, l’accélération de la pesanteur et de la pression P(0) au niveau du sol. dP(z) / dz = -m(z) g. Pourquoi g peut-elle être considérée comme constante ? La valeur maximale de z est 11 km : don z/R est négligeable devant 1 et g peut être considéré comme constant dans la troposphère.

retour -menu