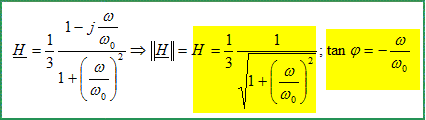Dipôle RC : régime transitoire, impédance complexe, diagramme de Bode concours Mines 07

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

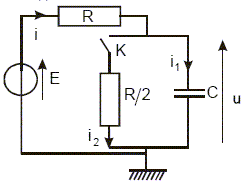
Nous considérons le circuit ci-dessous. Nous noterons i, l’intensité dans le résistor de résistance R, i₁ l’intensité dans le condensateur de capacité C, i₂ l’intensité dans le résistor de résistance ½R et u(t) la tension aux bornes du condensateur. L’interrupteur est ouvert depuis très longtemps.

A l’instant t=0, pris pour origine des temps, nous fermons l’interrupteur K.

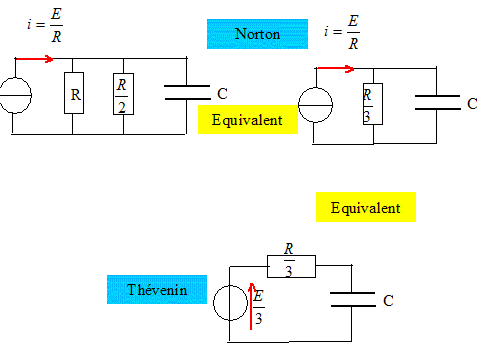
Préciser i, i₁, i₂ et u à l'instant t₀^-, juste avant la fermeture de l’interrupteur.

i₂ = 0 : la branche contenant le résistor ½R est ouverte.

i = i₁=0 : le condensateur chargé se comporte comme un interrupteur ouvert.

u(t) = E.

Préciser i, i₁, i₂ et u à l'instant t₀⁺.

La continuité de la tension conduit à u(t₀⁺)= u(t₀^-)=E.

i=0 : i₂=-i₁ =2E/R.

Même question quand t tend vers l’infini.

Le condensateur déchargé se comporte comme un interrupteur ouvert : i₁=0

i=i₂ = 2E/ (3R) ; u = E/3.

Montrer en transformant le réseau que le circuit est équivalent à un simple circuit RC en charge dont on précisera les caractéristiques. 

Le générateur de Norton équivalent au générateur de Thévenin ci-dessus est :

En déduire l’équation différentielle vérifiée par u(t) ainsi que la solution u(t).

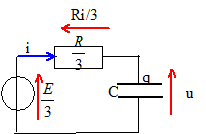
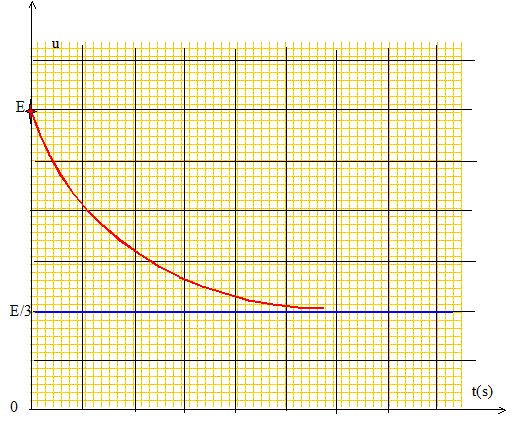
additivité des tensions : E/3 = Ri/3 + u avec i = dq/dt et q= Cu soit i= Cdu/dt

E/3 = RC/3du/dt + u ; du/dt + 3/(RC) u = E/(RC)

On pose t = RC/3, constante de temps du dipôle, d'où l'équation différentielle : du/dt + u/t = E/(RC) (1)

Solution générale de l'équation sans second membre : u(t) = A exp(-t/t)

Solution particulière ( régime permanent) : u= E/3

Solution générale de (1) : u(t) =A exp(-t/t) +E/3

à t = 0, u(0) = E d'où E= A+E/3 soit A = 2E/3.

u(t) = E/3 [1+2exp(-t/t) ].

Tracer l’allure de u(t).

L’interrupteur est fermé et nous remplaçons le générateur de f.e.m constante par une source idéale de tension de f.e.m. e(t) = 2^½E cos (wt) où w représente la pulsation du générateur et E, la tension efficace. On associe le complexe u=2^½U exp(j( wt +j)) = Uexp(j wt) à la tension u(t). De même E= 2^½E

Calculer la fonction de transfert, H=U/E que l’on écrira sous la forme H=H₀/(1+jw/w₀).

Impédance complexe du dipôle : Z = R/3 + 1/(jCw) ; impédance du condensateur :Z_C= 1/(jCw)

E /3 = Z I ; U = Z_C I.

H=U/E =Z_C / (3Z )=1/ [ 3 (1+jRCw/3 )]

On pose w₀ = 3/(RC) et H₀ = 1/3 d'où : H=H₀/(1+jw/w₀).

Préciser le module H et le déphasage j.

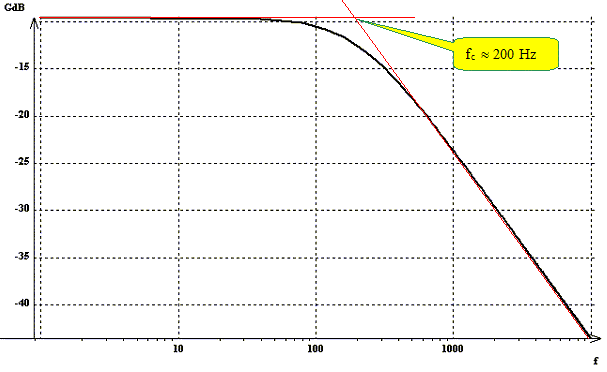
Etablir l’expression littérale de la fréquence de coupure f_c en fonction de R et C.

Le gain en décibel est égal à : G_dB = 20 log H = 20 log (1/3) -10 log [ 1+(w/w₀)²]

A la fréquence de coupure à 3 dB : H = H_max *2^-½ ; H_max = 1/3

20 logH= 20 log (1/3)-10 log 2=20 log(1/3) -3

d'où :10 log [ 1+(w/w₀)²] = 3

log[ 1+ (w/w₀)² ] = 0,3 ; 1+ (w/w₀)² = 2 ; (w/w₀)² =1 ; w=w₀=3/(RC).

f = w/(2p)=3/(2pRC) 

Nous traçons le diagramme de Bode en fonction de la fréquence f en échelle semi-log.

Déterminer graphiquement la valeur de f_c en précisant la méthode utilisée.

En déduire la valeur de la capacité C si R= 1,0 kW.

f_c=3/(2pRC)  soit C = 3/(2pR f_c)

C=3/(6,28*1000*200)=2,4 10^-6 F.