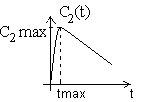|
Boire ou conduire... Cinétique de décomposition de l'alcool concours mines 06 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Il n’est autorisé à conduire que si la teneur en alcool de son sang est inférieure à 0,5 g.L-1. La cinétique de décomposition de l’alcool se fait en deux phases et peut être modélisée de la façon suivante : 1ère phase : passage de l’alcool à travers la paroi stomacale dans le sang. 2ème phase : oxydation de l’alcool dans le sang. Passage de l’alcool à travers la paroi stomacale dans le sang. La réaction peut se modéliser de la façon suivante : CH3CH2OH estomac --> CH3CH2OH sang On adopte les conventions suivantes : - l’estomac est considéré comme un milieu réactionnel de volume constant V1 égal pour chaque expérience au volume d’alcool absorbé. - on note [CH3CH2OH estomac] = C1 = C0 – x ; (C0 étant la concentration initiale, c’est à dire au moment de l’absorption) On réalise l’expérience suivante : un homme boit 250 mL d’un apéritif contenant 1 mole d’éthanol. On mesure la concentration C1 de l’éthanol dans l’estomac en fonction du temps. Les résultats sont regroupés dans le tableau ci-dessous :
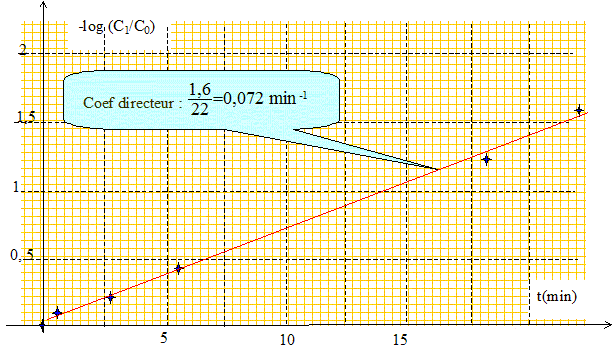
Définir la vitesse de disparition de l’alcool dans l’estomac. Cette vitesse sera notée v1. v1 = 1/V1 dx/dt = -d[CH3CH2OH estomac]/dt = -d(C0 – x/V1 )/dt avec x : avancement (mol) Montrer que v1 suit une loi cinétique d’ordre 1. Déterminer la valeur de la constante de vitesse k1 (sans oublier son unité !)
Pour le graphe on peut utiliser le logarithme décimal ou le logarithme népérien : le calcul de la constante k1 doit êtrte fait à partir du logaritme népérien. C1=C0 exp(-k1t) avec k1 = 0,072 *2,3 = 0,166 min-1. Le sang et les autres liquides contenus dans le corps seront considérés comme un milieu réactionnel unique, dénommé « sang », de volume V2 = 40 L constant pour toutes les expériences. Calculer la concentration C2 de l’alcool dans le sang à t = 18 min dans le cas où on admet qu’aucune oxydation de l’alcool ne s’est produite. C2 = x/ V2 avec
C0 – x/V1
=C18 et V1 = 0,25 L. x = (C0 –C18)
V1 = (4-0,2)*0,25 =0,95 mol C2 = x/ V2 =0,95/40 =2,375
10-2 = 2,4
10-2 mol/L. Démontrer la relation existant entre la vitesse de disparition de l’alcool dans l’estomac et la vitesse d’apparition, notée v, de l’alcool dans le sang en fonction de V1 et V2. Vitesse de disparition de l'alcool dans l'estomac : v1 = 1/V1 dx/dt = -d[CH3CH2OH estomac]/dt avec x : avancement (mol) ; dx/dt = v1 V1 Vitesse de d'apparition de l'alcool dans le sang : v = 1/V2 dx/dt v = V1 /V2 v1.
Oxydation de l'alcool dans le sang. On injecte directement une certaine quantité d’alcool dans le sang et on détermine la concentration en fonction du temps. (on suppose que l’injection est instantanée et que la concentration de l’alcool dans le sang est uniforme)
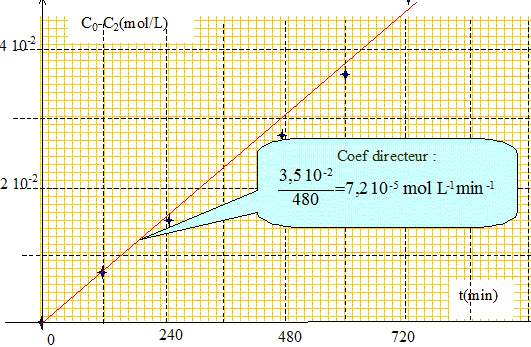
Définir la vitesse d’oxydation de l’alcool dans le sang. Cette vitesse sera notée v2. v2= 1/V2dx/dt = - dC2/dt Montrer que l’oxydation suit une loi cinétique d’ordre 0, c’est à dire que v2 = k2. Déterminer k2 (avec son unité !)
Pour déterminer le temps que la personne devra attendre avant de conduire, on est amené à étudier le phénomène absorption-oxydation de l’alcool dans son ensemble. On fait alors l’hypothèse simplificatrice que les lois de vitesse démontrées séparément restent valables. Calculer la concentration maximale, en mol.L-1, tolérée en France de l’alcool dans le sang. (La masse molaire de l’éthanol vaut 46 g.mol-1, et le taux maximal d’alcoolémie est fixé à 0,5 g.L-1). titre massique (g/L) / masse molaire ( g/mol) =0,5/46 = 1,087 10-2 = 1,1 10-2 mol/L. Exprimer la vitesse d’apparition de l’alcool dans le sang, dC2/dt, en fonction des vitesses v et v2 puis en fonction de la concentration C1 de l’alcool dans l’estomac au temps t, des constantes k1 et k2, des volumes V1 et V2. Rappels : C1=C0 exp(-k1t) ; C2 =C0 -k2t. Vitesse de d'apparition de l'alcool dans le sang à partir de l'estomac : v = V1 /V2 v1 ; v1 = -dC1/dt. d'où v = V1 /V2 C0k1exp(-k1t). vitesse d'oxydation de l'alcool dans le sang v2 = - dC2/dt = k2. Vitesse de d'apparition de l'alcool dans le sang : dC2/dt = v-v2. dC2/dt = V1 /V2 C0k1exp(-k1t) - k2 (1)
Intégrer l'expression précédente (1) : C2= -V1 /V2 C0exp(-k1t) – k2t + Cte. à t = 0 ( prise de la boisson) : C2=0. d'où Cte = V1 /V2 C0 et C2= V1 /V2 C0(1-exp(-k1t) )– k2t. (2) En buvant ses 2 bières à 8% notre homme absorbe 66 cL et 0,9 mole d’alcool. Déterminer l’instant, tmax, pour lequel la concentration en éthanol est maximale dans le sang. Dériver (2) par rapport au temps et chercher la valeur du temps qui annule cette dérivée. Il s'agit d'un maximum car à t=0 et au bout d'un temps très long, l'alcool a disparu du sang. V1 /V2 C0k1exp(-k1tmax) - k2 =0 exp(-k1tmax) = k2V2 / (V1 C0k1 ) ; tmax = -1/k1 ln[ k2V2 / (V1 C0k1 )]. k1 =0,166 ; k2 = 7,2 10-5; V2 = 40 L ; V1 C0 =0,9 mol. tmax= -1/0,166 ln [ 40* 7,2 10-5 / (0,9*0,166)] = 24 min.
Calculer cette concentration maximale. Peut-il conduire ? C2= V1 /V2 C0(1-exp(-k1t) )– k2t. C2 = 0,9/40 ( 1- exp(-0,166*24) - 7,2 10-5*43 = 2,21 10-2 - 3,096 10-3 = 1,90 10-2 mol /L = 0,02 mol/L. soit 46*1,90 10-2 = 0,87
g/L : la conduite est impossible.
On remarquera que au delà de tmax la courbe peut s’apparenter à une droite. Quelle est la pente de cette droite ? C2= V1 /V2 C0(1-exp(-k1t) )– k2t. Dans cette expression, à t >tmax, le terme contenant l'exponentielle est négligeable devant 1. d'où C2 = V1 /V2 C0– k2t, droite de pente -k2. En déduire le temps au bout duquel notre homme pourra reprendre sa voiture. C2 = 0,9/40 - 7,2 10-5 t = 2,25 10-2 - 7,2 10-5 t La conduite devient possible dés que C2 est inférieur ou égal à 1,1 10-2 mol/L. t =( 2,25 10-2 -1,1 10-2) / 7,2 10-5 = 160 min = 2,7 heures.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|