|
thermodynamique : étude d'un moteur à essence, rendement, bilan entropique concours mines 06 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
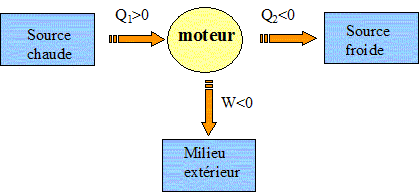
Les contraintes de fabrication et d’utilisation imposent de ne pas dépasser une pression de 50 bars dans le cylindre. Dans tout le problème, les gaz, quels qu’ils soient, sont assimilés à des gaz parfaits de rapport g = 1,4 et R = 8,314 J K-1 mol-1. Les transformations seront considérées comme mécaniquement réversibles. Questions préliminaires sur les moteurs thermiques. En 1824, Carnot postulait le principe suivant « Pour qu’un système décrive un cycle moteur, il doit nécessairement échanger de l’énergie avec au moins deux sources à des températures différentes… » Justifier le fait qu’un cycle monotherme ne puisse être moteur. Premier principe : la variation d'énergie interne est nulle sur le cycle. DU=W+Q=0. Second principe : la variation d'entropie est nulle sur le cycle. DS=Séchange+ Scréée=Q/T +Scréée = 0 Or l'entropie créée est positive, en conséquence Q est négatif. Or W=-Q ce qui entraîne W >0, c'est à dire un récepteur et non pas un moteur. On considère un système décrivant un cycle moteur ditherme. La machine reçoit de la source chaude S1, à la température T1, le transfert thermique Q1 et de la source froide S2, de température T2, le transfert thermique Q2. A quelle condition le rendement d’un tel moteur est-il maximal ? Le rendement est maximal lorsque le cycle est décrit de manière réversible. Définition et expression du rendement. h = -W/Q1. Premier principe : W+Q1+Q2=0 soit W= -(Q1+Q2) h =1+Q2/Q1. Second principe : DS= Séchangée + Scréée = 0 avec Scréée = 0, pour un sytème réversible. Q1/T1 + Q2/T2 = 0 ; Q2/Q1 = -T2/T1. h =1-T2/T1. Dans quels sens s’effectuent les transferts thermiques ? Quels sont les signes de Q1 et Q2 ? Justifier. (pour cette justification on pourra se placer dans le cas de la réversibilité) Q1/T1 + Q2/T2 = 0 soit Q1 = -Q2T1/T2 W+Q1+Q2=0 soit W + Q2(-T1/T2 +1)=0. W < 0 ; T1>T2 ; 1-T1/T2 <0 : donc Q2<0. Q1 = -Q2T1/T2 donc Q1 >0.
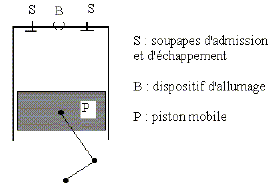
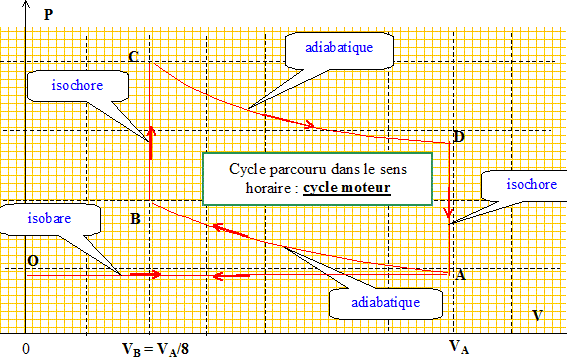
Dans le cas où le cycle n'est pas réversible : Exprimer la création d’entropie Scréée sur un cycle en fonction de Q1, Q2, T1 et T2. DScycle= Séchangée + Scréée = 0 avec Scréée > 0, pour un sytème irréversible. Séchangée = Q1/T1 + Q2/T2 ; Scréée = -(Q1/T1 + Q2/T2 ). Déterminer alors le rendement du moteur en fonction de T1, T2, Q1 et Scréée. h =1+Q2/Q1. Scréée = -(Q1/T1 + Q2/T2 ) ; Q2 = -T2 Scréée -Q1T2/T1 h =1 -T2/T1 -T2 Scréée /Q1. Le moteur à explosion. Le principe de fonctionnement est le suivant : O --> A : Phase d’admission. Le mélange gazeux est constitué d’air et de n’=2 10-4 mol d’essence. Il est admis de façon isobare à la pression PA dans le cylindre. La soupape d’admission est refermée. Le mélange air-carburant se trouve alors dans les conditions VA = 1 L, PA = 1 bar, TA = 293K= 20°C Le gaz subit alors la suite de transformations suivantes : • A-->B : compression adiabatique réversible. VB = VA/8 • B--> C : une étincelle provoque la combustion isochore, instantanée, de toute l’essence. • C-->D : détente adiabatique réversible ; on donne VD = VA ; • D -->A : refroidissement isochore. (la pression chute à cause de l’ouverture du cylindre vers l’extérieur) A-->O : refoulement isobare des gaz vers l’extérieur à la pression PA. C’est l’échappement. Dans toute l’étude de ce modèle de moteur à explosion, on suppose constant le nombre total de moles gazeuses. Représenter l’ensemble des transformations sur un diagramme ( P, V ). Indiquer le sens de parcours. Commenter.
Pourquoi parle-t-on de moteur à combustion interne ? La combustion du mélange air-essence a lieu à l'intérieur du cylindre. Pourquoi parle-t-on de moteur à 4 temps ? Préciser les 4 temps. temps n°1 : admission du mélange air-essence. temps n°2 : compression ; temps n°3 : combustion et détente ; temps n°4 : refroidisement des gaz puis refoulement de ces derniers à l'extérieur. Les étapes d’admission et de refoulement se compensent et on raisonnera donc sur le système fermé effectuant le « cycle » ABCD. Calculer nA, le nombre de moles de gaz initialement admis dans le cylindre. Le mélange air-carburant se trouve alors dans les conditions VA = 10-3 m3, PA = 105 Pa, TA = 293K nA = PA VA / (RTA) = 105 . 10-3 /(8,314 *298) = 4,036 10-2 mol = 4 10-2 mol. Le mélange gazeux est assimilé à un gaz parfait de rapport g = 1,4 Déterminer la pression du mélange dans l’état B. A-->B : compression adiabatique réversible. VB = VA/8 PA VA g=PB VBg. PB = PA(VA / VB)g = 105 *81,4 =1,838 106 Pa = 18 bar. Déterminer la température du mélange dans l’état B. PB VB = nARTB. TB =PBVB/ (nAR)=1,838 106. 10-3/(8*4,036 10-2*8,314) = 685 K On devrait en réalité prendre g= 1,34. Suggérer une justification. La valeur g=1,4 correspond au gaz diatomique ( O2, N2 ). Ici, il faut prendre en compte l'essence. Le mélange air-essence s’enflamme spontanément à 330°C, ce que l’on souhaite éviter … Calculer le taux de compression t = VA/VB maximal permettant d’éviter cet « autoallumage » entre A et B. Pour l’application numérique de cette question - uniquement - on prendra g = 1,34. A-->B : compression adiabatique réversible. VB = VA/8 TA VA g-1 =TB VBg-1. t = VA/VB = (TB/TA)1/(g-1) avec TB = 273+330 = 603 K. tmax = (603/293)1/0,34 = 8,4.
Calculer PC. Respecte-t-on la contrainte de pression mentionnée en introduction ? B--> C : une étincelle provoque la combustion isochore, instantanée, de toute l’essence. VB=VC= VA/8. PC VC = nARTC. PC= nARTC/VC = 8nARTC/VA = 8*4,038 10-2*8,31*2100 / 10-3 =5,637 106 Pa = 56 bar. En réalité la pression maximale est légèrement inférieure. Proposer une justification. La combustion du mélange air essence n'est pas instantanée. La pression est donc un peu inférieure à 56 bar et on respecte la contrainte imposée.( P<50 bar) Calculer la température en D. C-->D : détente adiabatique réversible ; on donne VD = VA ; TC VC g-1 =TD VDg-1. TC VB g-1 =TD VAg-1. TD =TC (VB /VA)g-1 =2100*(1/8)0,4 = 914 K. Exprimer, en fonction de Cv,m , n et des températures puis en fonction de n, R, g et des températures, le travail fourni par le gaz au système mécanique au cours d’un cycle. Le calculer. Cv,m représente la capacité thermique molaire à volume constant du mélange gazeux. • A-->B : compression adiabatique réversible. QAB=0. DUAB= WAB+QAB = nCv m (TB-TA). WAB=nCv m (TB-TA). • B--> C : combustion isochore. dW = - PdV ; WBC=0 ( volume constant) • C-->D : détente adiabatique réversible ; WCD=nCv m (TD-TC). • D -->A : refroidissement isochore. WDA=0 ( volume constant) Wcycle =nCv m(TB-TA+TD-TC). Or Cv m = R/(g-1) d'où : Wcycle =nR/(g-1) (TB-TA+TD-TC). Wcycle = 4,036 10-2*8,314/ 0,4 *(685-293+914-2100) = -666 J.
Définir le rendement du cycle, l’exprimer en fonction des différentes températures, le calculer. rendement = travail récupéré / énergie libérée par la combustion du mélange air-essence h= |W|/ QBC. La transformation B--> C est isochore ; le travail mis en jeu est nul ; la variation d'énergie interne est égale à l'énergie libérée par la combustion. QBC= n Cv m ( TC-TB) = nR/(g-1) ( TC-TB) QBC= 4,038 10-2*8,314 /0,4*(2100-603) =1256 J. h = 666 / 1256 =0,53. Le moteur effectue 2500 cycles par minute. Quelle est sa puissance ? La calculer. Combien le piston effectue-t-il d’allers-retours par minute ? Travail pour 2500 cycles : 666*2500 J Puissance (W) = travail (J) / durée (s) P= 666*2500/60 = 27,7
kW. Bilan entropique. Le refroidissement isochore DA s’effectue au contact de l’atmosphère, à la température TA. Exprimer la variation d’entropie DS du gaz lors de cette transformation en fonction des différentes températures. La transformation est isochore. le travail mis en jeu est nul. dU=dQ=n Cv m dT. dS = dQ /T = n Cv m dT / T = n Cv m d (ln T) DS = n Cv m ln(TA/TD). DS = n R/(g-1) ln(TA/TD). DS =4,036 10-2*8,314/0,4 ln(298/914) = -0,94 J K-1. Exprimer l’entropie échangée. Séchangée = QDA/TA =n Cv m (1-TD/ TA). Séchangée = n R/(g-1) (1-TD/ TA). Séchangée = 4,036 10-2*8,314/0,4 (1-914/293)= -1,78 J K-1. En déduire l’entropie créée au sein du mélange gazeux, la calculer. Scréée =DS - Séchangée. Scréée = -0,94+1,78 = 0,84 J K-1. Commenter le résultat : quelle est la cause d’irréversibilité ? L'entropie créée est positive : la transformation est irréversible. Les températures entre le système et l'extérieur sont différentes. Y-a-t-il eu création d’entropie au sein du gaz lors des évolutions : AB, BC et CD ? Dans l’affirmative, quel type d’irréversibilité en est la cause ? Les transformations AB et CD sont adiabatiques et réversibles : Scréée = 0. La transformation BC est irréversible Scréée > 0 : la combustion du mélange air-essence est irréversible.
|
|||||||
|
|
|||||||
|
|