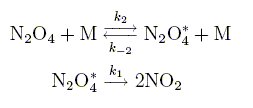|
Les oxydes d'azote :acide base, oxydoréduction, cinétique de décomposition du tétroxyde d'azote concours Mines 05 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
Donner les structures électroniques des atomes d’azote, N (Z = 7) et d’oxygène, O (Z = 8), dans leur état fondamental. Lequel de ces deux éléments est le plus électronégatif ? N : 1s2 2s2 2p3 ; O : 1s2 2s2 2p4 ; L'élément oxygène est plus électronégatif que l'élément azote. Le diazote, N2, constituant principal de l’atmosphère, est un gaz incolore. Donner la structure de Lewis de cette moécule.
Sachant que la molécule de protoxyde d'azote, N2O, possède un moment dipolaire m = 5,6.10-31 Cm, montrer qu'aucune des deux formes de Lewis suivantes de la molécule ne peut rendre compte à elle seule de la valeur de son moment dipolaire.
m= e d = 1,602.10-19 *120 10-12 = 1,9 10-29 Cm, très supérieur à la valeur réelle. Expliquer alors pourquoi, la structure réelle de la molécule est représentée par une superposition des deux formes précédentes. Données : les longueurs des liaisons dans la molécule sont proches de 120 pm, la charge élémentaire e = 1,602.10-19 C.
Solutions aqueuses et oxydo–réduction. Donner le nombre d’oxydation de l’azote dans chacun des oxydes d’azote suivants : NO3-, NO2, HNO2 et NO. NO3- : n.o(N) + 3n.o(O)=-1 ; n.o(N)+2*(-2)=-1 ; n.o(N)=+V. NO2 : n.o(N) + 2n.o(O)=0 ; n.o(N)+2*(-2)=0 ; n.o(N)=+IV. HNO2 : n.o(H)+n.o(N) + 2n.o(O)=0 ; 1+n.o(N)+2*(-2)=0 ; n.o(N)=+III. NO : n.o(N)+n.o(O)=0 ; n.o(N)+(-2)=0 ; n.o(N)=+II. Ecrire
l’équation bilan de la réaction
d’équilibre acido-basique de
l’acide nitreux sur l’eau. HNO2 +H2O
=NO2-
+H3O+. Exprimer sa constante
d’équilibre en fonction des
concentrations des espèces mises en
jeu. Ka
=[NO2-][H3O+]
/ [HNO2]. Lors du dosage par conductimétrie de l’acide nitreux par de la soude concentrée, on observe, avant le point d’équivalence, une croissance quasi linéaire de la conductivité en fonction du volume de soude versé, puis, après l’équivalence, une autre variation linéaire plus importante que la précédente. Interpréter ces faits. HNO2 + HO- +Na+---> NO2-+ +Na+ +H2O. La soude étant concentrée, le volume de la solution du becher est pratiquement constant, égal à Va.
conductivité s =lNa+ [Na+]+lNO2- [NO2-] + lHO- [HO-] = lNa+ x /Va+lNO2- x/Va = [ lNa++lNO2-] x /Va ; s= [ lNa++lNO2-]cbVb/Va ; droite , coefficient directeur positif. après l'équivalence, HO- est en excès : conductivité s =lNa+ [Na+]+lNO2- [NO2-] = lNa+ x /Va+lNO2- xéq/Va + lHO- (x-xéq)/Va= [ lNa++lHO-] x /Va +[lNO2--lHO-]xéq/Va Or droite lHO- >> lNO2- , droite de coefficient directeur positif, supérieur au coefficient directeur précédent.
2 NO2(g)+ aH2O = bNO3-(aq) +gNO2- +dH+ (aq) Equilibrer l’équation bilan de cette réaction de dismutation. 2 NO2(g)+ H2O = NO3-(aq) +NO2- (aq) +2H+ (aq). Exprimer sa constante de réaction K en fonction de la pression partielle, PNO2 en bar, du dioxyde d’azote et des concentrations des espèces en solution aqueuse. K = [H+]2[NO3-][NO2-] / P2NO2. Calculer, à partir des données, la valeur de K à 25 °C. E°(NO3-(aq)/NO2(g) )=0,83 V ; E°(NO2(g)/NO2- (aq) )=0,83 V à pH=0. NO2(g) + e- =NO2- (aq) (2) E2= E°(NO2(g)/NO2- (aq) ) + 0,06 log (PNO2 / [NO2- (aq)]). A l'équilibre E1=E2 : E°(NO3-(aq)/NO2(g) + 0,06 log ([NO3-(aq)][H+]2 / P(NO2(g)))= E°(NO2(g)/NO2- (aq) ) + 0,06 log (PNO2 / [NO2- (aq)]). E°(NO2(g)/NO2- (aq) ) - E°(NO3-(aq)/NO2(g) =0,06 log ([NO3-(aq)][NO2- (aq)][H+]2 / P2(NO2(g)))= 0,06 log K log K =( 0,85-0,83)/0,06 = 1/3 ; K = 2,1.
Une atmosphère de pression totale 1 bar, chargée en dioxyde d’azote, se trouve en équilibre avec une eau de pH = 4, l’acidité provenant de la réaction de dismutation de NO2 dans l’eau. Déterminer la pression partielle, PNO2 en bar, du dioxyde d’azote. K =2,1= [H+]2[NO3-][NO2-] / P2NO2. A pH >pKa, la forme base NO2- est majoritaire par rapport à la forme acide HNO2. 2 NO2(g)+ H2O = NO3-(aq) +NO2- (aq) +2H+ (aq). [NO3-]= [NO2-] = ½[H+] 2,1 =0,25 [H+]4 / P2NO2 ; P2NO2 = 0,25 [H+]4 /2,1 ; PNO2 =½[H+]2/2,1½ = 3,4 10-9 bar. En déduire la fraction molaire, xNO2, du dioxyde d’azote contenue dans l’atmosphère. xNO2 = 3,4
10-9.
Le tétroxyde d'azote se décompose en phase gazeuse en dioxyde d'azote suivant la réaction globale N2O4 = 2NO2. En supposant que la réaction corresponde à un acte élémentaire, indiquer l’influence de la concentration sur la vitesse de décomposition. Déterminer, dans cette hypothése, l’expression théorique de la concentration [N2O4] dans le réacteur en fonction du temps t, de la concentration initiale [N2O4]0 et de la constante de vitesse k de la réaction. vitesse de la réaction : -d[N2O4] /dt= k [N2O4] d[N2O4] / [N2O4] =-kdt puis intégrer. ln[N2O4]-ln[N2O4]0 = -kt ou [N2O4] =[N2O4]0 exp(-kt). En réalité, il apparaît que la vitesse de réaction dépend non seulement de la concentration en réactif mais aussi de la concentration totale des espéces gazeuses présentes dans l’enceinte ou, ce qui revient au même, de la pression totale. Ceci se manifeste, en particulier, par un changement de l’ordre global de la réaction qui peutpasser de un à deux lorsque la pression totale P varie. Ce comportement assez fréquent dans les réactions unimoléculaires en phase gazeuse s’explique à l’aide du mécanisme de Lindemann–Hinshelwood suivant :
Dans ces différentes étapes M désigne une molécule quelconque (réactif, produit ou toute autre espèce gazeuse présente dans l'enceinte). N2O4* est une mol¢¥ecule de tétroxyde d'azote qui a acquis suffisamment d¡énergie par collision pour pouvoir se décomposer. Donner l'expression de la vitesse d'apparition de l'intermédiaire réactionnel N2O4*. d[ N2O4*]/dt =k2[N2O4][M]-k-2[ N2O4*][M]-k1[ N2O4*] Déterminer sa concentration, [ N2O4*] à l'aide du principe de létat quasi stationnaire, en fonction de k1, k2, k-2, [M] et [N2O4]. d[ N2O4*]/dt =0 ; k2[N2O4][M] =[ k-2[M]+k1][ N2O4*] [ N2O4*] =k2[N2O4][M] / (k-2[M]+k1).
Montrer que la vitesse de réaction se met sous la forme v = k[N2O4] où k est la constante de réaction unimoléculaire que l’on exprimera en fonction de k1, k2, k-2 et [M]. vitesse de réaction v = ½ d[NO2]/dt = k1[ N2O4*] v = k1k2[N2O4][M] / (k-2[M]+k1) =k1k2[N2O4] / (k-2+k1/[M]) On pose k = k1k2 / (k-2+k1/[M]). Donner, à faible pression, l'expression approchée k0 de k en fonction de k2 et [M]. Quelle est la molécularité de la réaction globale ? Les collisions avec les molécules M sont peu probables : k-2[M]<<k1 k0 = k2[M] ; v = k2[M] [N2O4] bimoléculaire. Inversement, à haute pression, déterminer l'expression koo de k. Que devient la molécularité de la réaction globale ? Les collisions avec les molécules M sont fréquentes : k-2[M]>>k1 koo = k1k2 / k-2 ; v = k1k2 / k-2 [N2O4] momoléculaire.
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
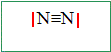

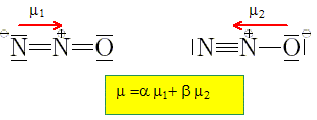 a,
b constantes.
a,
b constantes.