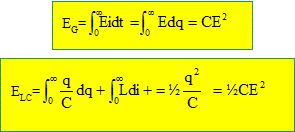Dipôle RLC série soumis à un échelon de tension concours Mines 05

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

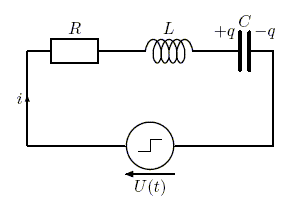
U(t) = (0 pour t < 0, E pour t = 0.

Les choix du sens du courant i dans le circuit et de la plaque portant la charge q du condensateur sont donnés sur la figure ci-dessous.

On pose : g=R/(2L) et w₀=(LC)^-½.

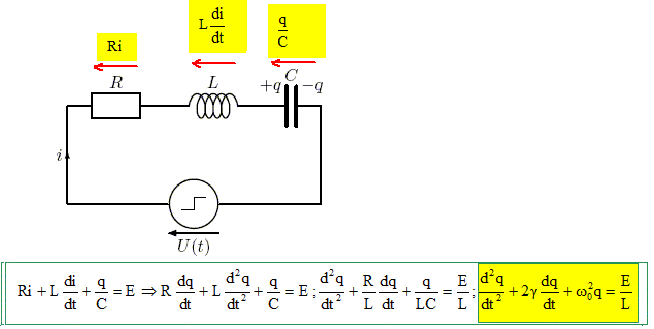
Expliquer simplement pourquoi à t = 0^- la charge q et le courant i sont nuls.

Si t <0 alors U(t) =0.

La bobine se comporte comme un interrupteur fermé : donc u_L=0

Le condensateur se comporte comme un interrupteur ouvert : donc i=0.

La tension aux bornes du résistor u_R=Ri=0.

Additivité des tensions : u_R+u_L+u_C=0 : donc u_C=0.

Le condensateur est déchargé q=u_C/C=0.

Etablir l’équation différentielle vérifiée par la charge q(t) du condensateur pour t > 0.

Préciser, en les justifiant soigneusement, les valeurs initiales de la charge q(0⁺) et de sa dérivée dq/dt(0⁺).

La continuité de la charge du condensateur s'écrit : q(0+) = q(0-) =0 La continuité de l'intensité dans une boine inductive s'écrit : i(0+) = i(0-) =0 avec i(0+) =dq/dt(0+)

Le circuit présente différents régimes suivant les valeurs de R, L et C.

On suppose, dans la suite, la condition w₀>g réalisée.

Montrer que l’expression de la charge pour t > 0 peut se mettre sous la forme :

q(t) = (A cos(wt)+Bsin(wt) exp(-gt)+D.

Equation caractéristique associée à l'équation différentielle sans second membre. r2+2g r+ w02=E/L Discriminant réduit : D'= g2-w02= j2w2 avec j2=-1. solutions : r1 = -g + jw ; r1 = -g - jw d'où q(t) = A exp(r1t) + B exp(r2t) q(t) = A exp(-gt) exp(+jwt) + B exp(-gt)exp(-jwt) q(t) = exp(-gt) [Aexp(+jwt) +Bexp(-jwt) ]. Solution particulière de l'équation avec second membre : q=CE. Solution de l'équation différentielle avec second membre : q(t) = exp(-gt) [Aexp(+jwt) +Bexp(-jwt) ]+CE. q(t) = exp(-gt) [Acos(wt) +Bsin(wt) ]+CE.

Déterminer w, A, B et D en fonction de C, E, g et w₀.

w² =w₀²-g² ; D=CE ;

à t=0, q=0 : 0 = A+CE=0 ; A= -CE.

i=dq/dt = -gexp(-gt)[Acos(wt) +Bsin(wt) ] +exp(-gt)[-Awsin(wt) wBcos(wt) ]

à t=0, i=0 : -gA+wB=0 d'où B=Ag/w ; B= -CEg/w.

q(t) = -CEexp(-gt) [cos(wt) +g/wsin(wt) ]+CE.

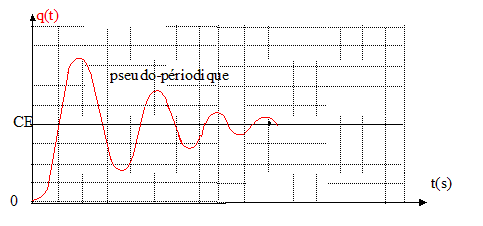
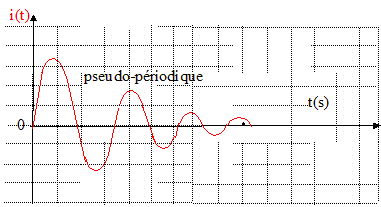
Exprimer le courant i(t) dans le circuit pour t > 0 en fonction de C, E, g et w₀.

i=dq/dt = CEgexp(-gt)[cos(wt) +g/wsin(wt) ] -CEexp(-gt)[-wsin(wt)+gcos(wt) ]

i(t) = CE exp(-gt)[ g²/w+w]sin(wt)

i(t) = CE w₀²/w exp(-gt) sin(wt).

Donner l’allure des courbes q(t) et i(t).

Quelles sont leurs valeurs à la fin du régime transitoire ?

Justifier par des considérations simples ces valeurs atteintes.

L'intensité est nulle : le condensateur se comporte comme un interrupteur ouvert.

La charge du condensateur est égale à CE, la tension à ces bornes vaut E.

La bobine se comporte comme un interrupteur fermé ; la tension à ses bornes est nulle.

Déterminer l’énergie totale E_G fournie par le générateur ainsi que l’énergie E_LC emmagasinée dans la bobine et le condensateur à la fin du régime transitoire en fonction de C et E.

En déduire l’énergie dissipée par effet Joule dans la résistance.

E_G-E_LC=½CE².

Ces résultats dépendent-ils du régime particulier dans lequel se trouve le circuit ?

Résultats indépendants du régime.

Interpréter le résultat paradoxal qui apparaît dans le cas limite R = 0.

Le circuit est oscillatoire périodique ( sans amortissement ).

Le condensateur et la bobine stockent tous deux de l'énergie.