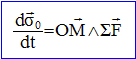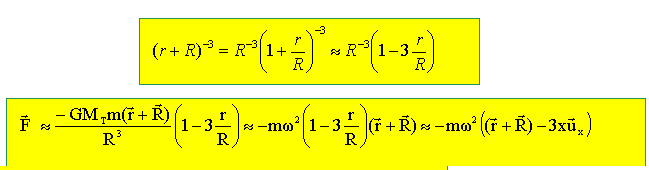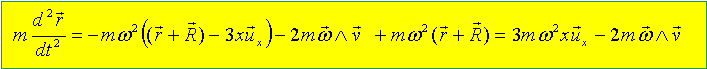mécanique : station spatiale, référentiel géocentrique, référentiel lié au satellite concours Mines 05

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

Une station spatiale est sur une orbite circulaire autour de la Terre. Son mouvement est étudié dans le référentiel géocentrique K, d'origine O considéré comme galiléen. La station est, dans cette partie, assimilée `a un point S de masse M_S, repéré par le rayon vecteur R=OS.

Enoncer le principe d'inertie en rappelant la définition d'un référentiel galiléen.

référentiel galiléen : dans ce référentiel le principe d'inertie ou 1^ère loi de Newton s'applique " un point matériel pseudo-isolé demeure dans son état de repos ou de mouvement rectiligne uniforme".

Définir le référentiel géocentrique.

Le référentiel héliocentrique a pour origine le Soleil et des axes pointant vers des étoiles lointaines qui paraissent fixes.

Le référentiel géocentrique a pour origine le centre de la Terre et des axes parallèles à ceux du référentiel héliocentrique.

Sur quelle échelle de temps ce référentiel peut-il être considéré comme approximativement galiléen ?

Sur des durées très inférieures à une année, le référentiel géocentrique peut être considéré en translation uniforme dans le référentiel héliocentrique.

Définir le moment cinétique s_O de la station S par rapport à l'origine O du référentiel.

s_O = OM^M_Sv = M_SR^v.

Montrer que ce vecteur forme une constante du mouvement.

Déduire que le mouvement du satellite s'effectue dans un plan que l'on définira à partir de s_O.

Nature du mouvement :

Le satellite est alors soumis à la force centrale F= GM_SM_T/R² u. u est un vecteur unitaire

Le référentiel d'étude étant galiléen :

La dérivée par rapport au temps du moment cinétique du point matériel M par rapport au point fixe O est égal au moment, par rapport à ce point, de la somme vectorielle des forces agissant sur le point matériel M .

Or OM et F sont colinéaires ; le produit vectoriel OM ^ F est nul ; en conséquence le moment cinétique s₀ est constant : le mouvement est plan, perpendiculaire à s₀.

Montrer d'autre part, que le mouvement circulaire du satellite s'effectue avec un vecteur vitesse angulaire w constant et dirigé suivant s₀ .

Le mouvement étant circulaire : v = w^R. Les vecteurs w et R sont de plus perpendiculaires.

 s_O = M_SR^v = M_SR^(w^R)= M_SR²w.

s_O et w sont des vecteurs colinéaires et de même sens. s_O étant un vecteur constant, il en résulte que w est un vecteur constant.

Exprimer w en fonction de la masse de la Terre, MT , de la constante de gravitation universelle, G et du rayon R. La 2è loi de Newton appliquée au satellite s'écrit : MSw2R= GMSMT/R2. w2= GMT/R3 ; w= [GMT/R3 ]½.

La station spatiale internationale en construction depuis 1998 est située à une altitude d’environ 400 km.

Calculer sa période de rotation T.

Rayon terrestre moyen R_T = 6400 km ; g₀ = 9,8 m s^-2.

g₀ =GM_T/R_T² ; w = 2p /T ; R=R_T+h.

d'où : w =2p /T =[g₀R_T²/R³ ]^½ ; T =2p [R³ /(g₀R_T²) ]^½.

R³ =(6,8 10⁶)³ =3,144 10²⁰ m³ ; g₀R_T²= 9,8*(6,4 10⁶)² =4,014 10¹⁴.

T =6,28(3,144 10²⁰/ 4,014 10¹⁴ )^½ ; T = 5,56 10³ s. 

La station spatiale est en rotation synchrone autour de la Terre ; elle tourne sur elle-même avec un vecteur vitesse angulaire identique à celui de son mouvement orbital, w.

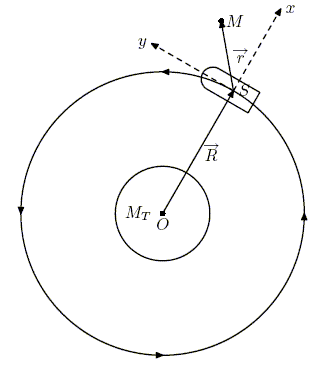
On désigne par K' le référentiel lié à la station. L'origine de ce référentiel est situé au centre de masse, S, de la station. L'axe Sx est dirigé suivant R, l'axe Sz est porté par le moment cinétique s_O et l'axe Sy complète le trièdre orthonormé.

Dans ce référentiel, un corps ponctuel M, de masse m, est en mouvement dans le plan Sxy. Il est repéré dans la station par le rayon vecteur r = SM.

Pourquoi le référentiel K' n'est-il pas galiléen ?

K' n'est pas animé d'un mouvement de translation uniforme par rapport au référentiel géocentrique.

Définir le point coïncident à M et donner son accélération a_e(M) en fonction de r, R et w. 

En déduire la force d’inertie d’entraînement f_e exercée sur la masse m dans K'.

Si la particule M est animée d'une vitesse v dans K', quelle force d'inertie supplémentaire lui est appliquée ?

Exprimer cette force en fonction de m, w et v.

La particule se trouvant dans le voisinage proche de la station, l'inégalité r << R sera toujours vérifiée dans la suite du problème.

A l'aide d'un développement limité arrêté au premier ordre en r/R, montrer que la force d'attraction gravitationnelle qu'exerce la Terre sur le corps M s'écrit :

F = -mw²(R +r - 3x u_x).

où u_x est le vecteur unitaire porté par l'axe Sx et (x, y) sont les coordonnées de r dans K'.

Le corps M est une balle qu'un cosmonaute lance en direction de la Terre avec la vitesse relative v₀ =-v₀u_x (v₀ << wR) dans K' depuis l'origine S de ce référentiel.

Etablir l'équation du mouvement dans K' de la balle sous la forme de deux équations différentielles pour les variables x et y.

Ecrire la deuxième loi de Newton à la balle dans le référentiel K' :

Projections sur chaque axe :

mx"= 3mw²x+2mwy' ; x"-2wy' -3w²x =0. (1)

my"=-2mwx' ; y"+2wx'=0.(2)

Intégrer ces équations, montrer que la trajectoire suivie est une ellipse et déterminer sa période de parcours.

(2) donne y' = -2wx+Cte ; à t=0 y'=0, x=0 d'où Cte =0

y'=-2wx (3); repport dans (1)

x"+w²x =0.

x= A sin (wt) +B ; à t=0 , x=0 donc B=0

x' = Aw cos (wt) ; à t= x'=-v₀ d'où A=-v₀ /w

x= -v₀ /w sin (wt).

repport dans (3) : y'=2v₀sin (wt) ; y = -2v₀/w cos (wt)+ Cte.

à t=0, y=0 soit Cte =2v₀/w. y= 2v₀ /w[1- cos (wt)].

Ellipse de centre (0 ; 2v₀ /w) ; demi-grand axe : 2v₀ /w ; demi-petit axe v₀ /w ; période T = 2p/w.