Dosage d’une solution de glucose par la méthode de Bertrand ; acide tartrique ; liqueur de Fehling concours Mines 05

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

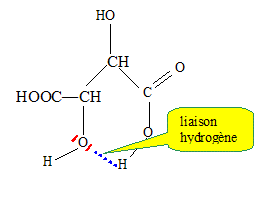
Cette méthode est utilisée pour doser des solutions de glucose, le principal réactif est la liqueur de Fehling. La liqueur de Fehling est préparée en mélangeant des volumes égaux :

• De la solution A contenant 3,5 mol/L d’hydroxyde de sodium et 1 mol/L de tartrate de sodium et potassium.

• De la solution B solution de sulfate de cuivre II.

Etude de l’acide tartrique :

Cet acide a pour formule brute : C₄H₆O₆. Il possède deux fonctions alcool et deux fonctions acide carboxylique.

L’acide tartrique (noté H₂T) se comporte comme un diacide en solution aqueuse dont les pK_a ont pour valeur : pK_a1 = 2,9 ; pK_a2 = 4,5.

Présenter la liaison hydrogène de manière succincte et évoquer son influence sur les valeurs des deux pK_a de l’acide tartrique.

La liaison hydrogène résulte de l'interaction entre un hydrogène lié à un atome très électronégatif et un atome d'azote, oxygène ou fluor, porteur de doublet non liant.

Cette liaison peut être intermoléculaire ou intramoléculaire. Dans ce dernier cas, le proton engagé dans une telle liaison est moins disponible, moins acide : cela explique la différence des deux pK_a.

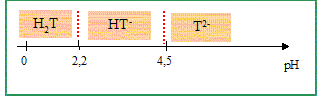
Tracer le diagramme de prédominance de l’acide tartrique en fonction du pH.

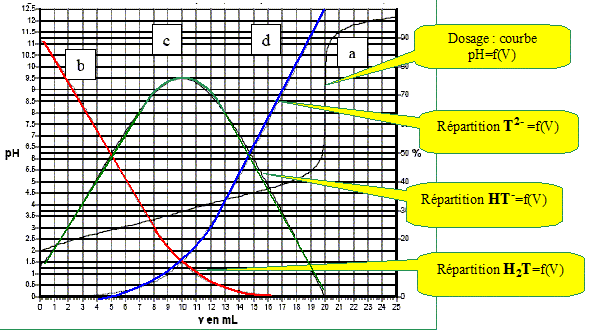
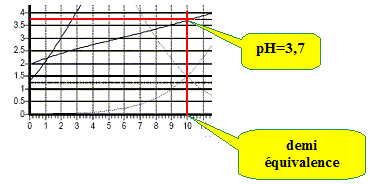
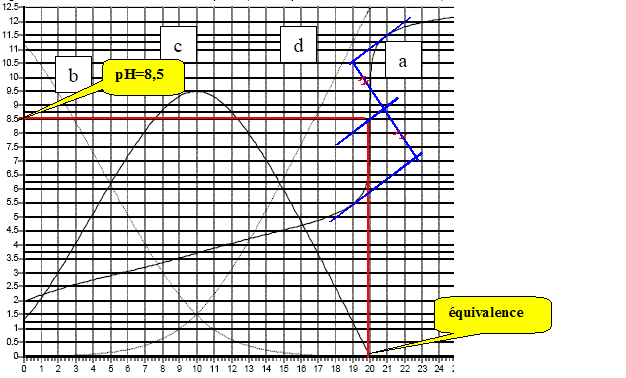
On dose 10 mL d’une solution d’acide tartrique à 0,1 mol/L par une solution de soude à 0,1 mol/L. On suit ce titrage par pHmétrie, les résultats expérimentaux sont reportés sur la figure ci-dessous. Par modélisation informatique on superpose à la courbe obtenue les courbes de répartition des espèces en fonction du pH.

Identifier ces courbes.

Le pH lu sur la courbe pH=f(v) pour v=0 mL est-il en accord avec l’hypothèse consistant à négliger la seconde acidité ?

Hypothèses : seconde acidité négligée, autoprotolyse de l'eau négligée.

	avancement volumique(mol/L)	H2T	+H2O	=HT-	+H3O+
initial	0	c	solvant en large excès	0	0
à l'équilibre	x	c-x		x	x

K_a1 =[H₃O⁺][HT^-] /[H₂T] = x² / (c-x) ; 10^-2,9 (0,1-x) =x² ; -1,26 10^-4 +1,26 10^-3 x + x²=0

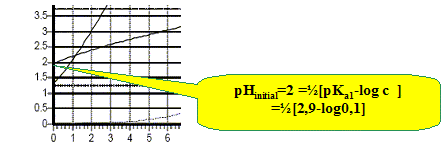
d'où x =1,06 10^-2 mol/L. (10 % de l'acide est donc dissocié )

hypothèse supplémentaire : c-x proche de c d'où : [H₃O⁺]² = K_a1 c ; pH = ½(pK_a1 -log c).

Combien de sauts de pH observe-t-on ? Cela est-il justifiable ?

Les deux pK_a étant proches, on observe un seul saut de pH.

Retrouver le pH de la solution lorsque 10 mL de la solution de soude ont été versés.

H₂T + HO^- =HT^-+H₂O ; HT^-+HO^- =T^2-+H₂O

K_a1 =[H₃O⁺][HT^-] /[H₂T] ; K_a2 =[H₃O⁺][T^2-] /[HT^-]

K_a1K_a2 =[H₃O⁺]²[T^2-] /[H₂T] (1)

	avancement (mol)	H2T	+2HO-	=T2-	+2H2O
initial	0	cV	cVb	0	solvant en large excès
demi équivalence	x	cV-x	cVb-2x	x

à la demi équivalence x = ½cV ; [H₂T]=½cV /(2V) =0,25 c ; [T^2-] =½cV /(2V) =0,25 c

(1) donne : K_a1K_a2 =[H₃O⁺]² ; pH=½(pK_a1 +pK_a2)= 0,5(2,9+4,5) =3,7.

Calculer le pH de la solution lorsque 20 mL de la solution de soude ont été versés.

A l'équivalence le couple acide base HT^-/T^2- fixe le pH.

T^2-+ H₂O = HT^- +HO^-. K = [HT^-][HO^-] / [T^2-]

avec [HT^-]= [HO^-] et [T^2-] proche de : cV/(V+2V) = c/3 mol/L

K = 3[HO^-]²/c ; [HO^-]²= Kc/3.(2)

de plus K_a2 =[H₃O⁺][T^2-] /[HT^-] soit[HT^-] /[T^2-] = [H₃O⁺] /K_a2.

Repport dans l'expression de K : K = [HO^-] [H₃O⁺] /K_a2= 10^-14/10^-4,5 = 10^-9,5.

(2) donne : [HO^-]²= Kc/3= 10^-9,5*0,1/3 =1,05 10^-11.

[HO^-]=3,24 10^-6 mol/L ; [H₃O⁺] =10^-14/3,24 10^-6 =3,1 10^-9 mol/L ; pH =8,5.

Peut-on calculer le pH de la solution avec le modèle que l’on a l’habitude d’utiliser ?

De la solution A contenant 3,5 mol/L d’hydroxyde de sodium et 1 mol/L de tartrate de sodium et potassium.

Dans le modèle habituel, les solutions sont diluées, ce qui n'est pas le cas de la solution A. Les calculs habituels ne s'appliquent pas à ce type de solution.

Quelles sont les espèces chimiques présentes dans cette solution, ainsi que leur concentration ?

[HO^-]=3,5 mol/L ; [T^2-] =[K⁺]= 1 mol/L ; [Na⁺]=3,5+1 = 4,5 mol/L.

Etude de la solution B :

La solution B est de couleur bleue, elle est parfaitement limpide. Cette couleur est due à la présence des ions tétraaquacuivre II Cu(H₂O)₄²⁺.

Nous désirons déterminer la concentration de cette solution B en sulfate de cuivre par spectrophotométrie.

Rappeler la loi de Beer-Lambert et préciser les unités.

La loi de Berr-Lambert exprime la variation de l'intensité lumineuse en fonction de la distance parcourue dans un milieu transparent.

Lorsqu'une lumière monochromatique d'intensité I₀ traverse un milieu homogène, l'intensité de la lumière émergente I décroît exponentiellement lorsque l'épaisseur l du milieu absorbant augmente.

I = I₀ . e ^{(- al)}

a est une constante appelée coefficient d'absorption, caractéristique du milieu et de la longueur d'onde considérés.

Dans le cas des solutions, la loi de Beer fait intervenir les concentrations.

I = I₀ . e ^{(- elc)}

où e est un coefficient caractéristique de la substance appelé coefficient d'absorbance (L mol^-1 cm^-1), l est l'épaisseur de la cuve (cm) et c la concentration de la solution (mol/L).

Cette loi est vérifiée lorsque la solution est de concentration inférieure à : c < 0,1 mol.L^-1.

La relation fondamentale utilisée en spectrophotométrie est présentée sous la forme :

A= log (I₀/I) = elc ( A est l'absorbance ou densité optique)

e est une caractéristique de la molécule. Plus e sera grand, plus la solution absorbe.

On considère que dans la solution étudiée, seuls les ions complexes tétraaquacuivre II absorbent.

Pour vérifier la loi de Beer-Lambert comment doit-on choisir la longueur d’onde utilisée ?

Les solutions colorées présentent une longueur d’onde lumineuse où l’absorption est maximale. Cette longueur d’onde maximale l _max ne dépend pas de la concentration, c’est une grandeur caractéristique de l’ion absorbant. Elle est utilisée pour effectuer les mesures photométriques sur des solutions de différentes concentrations.

Pour déterminer la concentration de la solution B en sulfate de cuivre II nous nous proposons d’utiliser la méthode des ajouts dosés.

Cette méthode consiste à prendre 100 mL de la solution B et d'ajouter successivement n₁=1,0.10^-3 mol de sulfate de cuivre II pentahydraté cristallisé (CuSO₄,5H₂O) cela sans variation de volume ce qui correspond à une concentration ajoutée c₁.

On obtient alors les résultats suivants pour la longueur d'onde l=800 nm :

Absorance An	0,24	0,32	0,40	0,48	0,56
concentration c0+nc1	c0	c0+c1	c0+2c1	c0+3c1	c0+4c1

Exprimer l’absorbance A_n en fonction de c₀, n, c₁.En déduire la concentration c₀ en sulfate de cuivre de la solution B.

A_n = k(c₀+nc₁) avec k : constante de proportionnalité.

A₀ = kc₀ =0,24 ; A₁ = A₀ + kc₁ ; k = (A₁-A₀)/c₁ avec c₁ = 1,0 10^-3/0,10 =1,0 10^-2 mol/L

k = 0,08 /1,0 10^-2 = 8,0 L mol^-1.

c₀ = A₀ / k = 0,24/8,0 = 3,0 10^-2 ; c₀ = 3,0 10^-2 mol/L.

On mélange 100 mL de la solution A avec 100 mL de la solution B.

Pour simplifier les calculs, nous ferons l'hypothèse que le pH de la solution obtenue est de 14, cette valeur sera invariable dans les questions suivantes.

Calculer les concentrations en tartrate (noté T^2-), en Cu ²⁺ et en ions hydroxyde de la solution après mélange, mais avant toute réaction.

Le facteur de dilution vaut 2 d'où :[T^2-] = 1/2 =0,5 mol/L ; [Cu²⁺]=½c₀ =1,5 10^-2 mol/L.

Déterminer les espèces présentes à l'équilibre ainsi que leur concentration. D'après les calculs la solution doit-elle rester limpide ?

Données : Cu(OH)₂ (s) : pK_s = 19,0 ; (CuT₂)^2- : log b₂ = 5,0

2HO^- + Cu²⁺ = Cu(OH)₂ (s) ; K_s=[Cu²⁺][HO^-]²=10^-19.

or [HO^-] = 1 mol/L et [Cu²⁺] =0,015 mol/L ; [Cu²⁺][HO^-]²=0,015.

valeur très supérieure à 10^-19, l'hydroxyde de cuivre précipite.

Cu(OH)₂ (s) + 2T^2- = (CuT₂)^2- + 2HO^- ; K = [HO^-]²[(CuT₂)^2-] / [T^2-]².

Or : Cu²⁺ + 2T^2- = (CuT₂)^2- avec 10⁵ = [(CuT₂)^2-] /([Cu²⁺][T^2-]²) soit : [(CuT₂)^2-] / [T^2-]² =10⁵[Cu²⁺]

repport dans l'expression de K : K = [HO^-]²10⁵[Cu²⁺] = 10^-19 * 10⁵ = 10^-14.

Or [HO^-] = 1 mol/L ; [(CuT₂)^2-] / [T^2-]² = 10^-14.

T^2- étant en large excès par rapport à Cu²⁺, [T^2-] proche de 0,5 mol/L

d'où : [(CuT₂)^2-] = 10^-14*[T^2-]² = 10^-14*0,25 = 2,5 10^-15 mol/L.

Expérimentalement nous observons une solution d'un bleu foncé. Conclure. Pourquoi doit-on préparer la liqueur de Fehling juste avant son utilisation ?

L'observation d'une teinte bleue indique la formation de l'ion complexe (CuT₂)^2-

La formation du précipité Cu(OH)₂ (s) doit être lente ( blocage cinétique). Pour avoir une solution limpide il faut préparer la liqueur de Fehling juste avant son utilisation.

Le glucose est un sucre réducteur de formule brute C₆H₁₂O₆. Il peut être oxydé à chaud en ion gluconate (C₆H₁₁O₇^-) par des oxydants doux tels que les ions cuivre II présents dans la liqueur de Fehling sous la forme d’ions complexes (CuT₂)^2- . On observe alors la formation d’oxyde de cuivre I solide de couleur rouge.

Analyse du protocole expérimental :

Verser dans un erlenmeyer de 150 mL, à col étroit , propre : 20 mL de la solution A, 20 mL de la solution B, 20 mL de la solution de glucose à doser.

Porter à ébullition pendant 3 min, laisser refroidir la fiole inclinée, vérifier que le liquide surnageant est bien bleu. Verser la quasi-totalité du liquide surnageant dans l’erlenmeyer sur le verre fritté, filtrer sous vide.

Rincer le solide rouge restant dans l’erlenmeyer avec de l’eau distillée bouillante, agiter ; laisser reposer, fiole inclinée. Décanter le liquide surnageant sur le verre fritté comme précédemment. Recommencer au moins 6 fois de suite cette opération.

Verser dans l’erlenmeyer 20 mL d’une solution d’alun de fer III (ammonium-fer III sulfate) acidifiée par l’acide sulfurique.

Agiter, on doit alors constater que la solution vire au vert et que le précipité d’oxyde de cuivre I est consommé.

Rincer la fiole à vide, verser alors sur le verre fritté la solution verte obtenue et aspirer sous vide.

Recommencer la même opération mais en prenant cette fois 10 mL de la solution de fer III, bien rincer les parois de l’erlenmeyer et faire passer sur le verre fritté.

La solution verte obtenue est titrée par une solution acide de permanganate de potassium à 0,02 mol.L^-1.

couple redox : C₆H₁₁O₇^- / C₆H₁₂O₆.

 C₆H₁₂O₆ +3HO^- = C₆H₁₁O₇^- + 2e^- +2H₂O (1) oxydation

couple redox : CuT₂^2- / Cu₂O(s)

2CuT₂^2-+ 2e^- +2HO^- = Cu₂O(s)+ 4T^2- +H₂O (2) réduction

 C₆H₁₂O₆ +5HO^- +2CuT₂^2-= C₆H₁₁O₇^- +Cu₂O(s)+ 4T^2- +3H₂O.

Calculer la constante thermodynamique K de cette réaction. Conclure.

Potentiels standard redox : Cu²⁺/Cu₂O : E°₁ = 1,02 V ; C₆H₁₂O₇ /C₆H₁₂O₆ : E°₂ = -0,24 V

K = [C₆H₁₁O₇^-][T^2-]⁴ /([CuT₂^2-]²[HO^-]⁵[C₆H₁₂O₆]) (3)

Or Cu²⁺ + 2T^2- = (CuT₂)^2- avec 10⁵ = [(CuT₂)^2-] /([Cu²⁺][T^2-]²) soit [T^2-]² / [(CuT₂)^2-] =10^-5 /[Cu²⁺].

Repport dans (3) : K = [C₆H₁₁O₇^-]10^-10 /([Cu²⁺]²[HO^-]⁵[C₆H₁₂O₆]) (4)

Or couple : Cu²⁺/Cu₂O

2Cu²⁺+ 2e^- +H₂O = Cu₂O(s)+2H⁺ (5) réduction

et couple redox : C₆H₁₂O₇ / C₆H₁₂O₆.

 C₆H₁₂O₆ +H₂O = C₆H₁₂O₇ + 2e^- +2H⁺ (6) oxydation

(5) et (6) donnent : 2Cu²⁺+ C₆H₁₂O₆ +2H₂O = Cu₂O(s)+4H⁺+C₆H₁₁O₇

K₁=[C₆H₁₂O₇][H⁺]⁴/([C₆H₁₂O₆][Cu²⁺]²) (7) avec ln K₁ = 2F/(RT) (E°₁-E°₂ ) =2*96500/(8,31*298) *1,26=98,2 ; K₁ =4,4 10⁴².

(7) donne : [C₆H₁₂O₆][Cu²⁺]² = [C₆H₁₂O₇][H⁺]⁴/K₁.

repport dans (4) : K =K₁ [C₆H₁₁O₇^-]10^-10 /([C₆H₁₂O₇][H⁺]⁴[HO^-]⁵)

produit ionique de l'eau :[H⁺][HO^-] = 10^-14.

K =K₁ 10^-10 [C₆H₁₁O₇^-][H⁺] /([C₆H₁₂O₇] 10^-70)

Or [C₆H₁₁O₇^-][H⁺] /([C₆H₁₂O₇] = K_a =10^-5 du couple acide base C₆H₁₂O₇/C₆H₁₁O₇^-

K =K₁ 10^-10K_a 10⁷⁰ = 4,4 10⁴² .10^-10. 10^-5 .10⁷⁰ ; K = 4,4 10⁹⁷, valeur élevée de cette constante, la réaction est totale.

Ecrire l’équation de la réaction de l’oxydation des ions fer II par les ions permanganate.

Fe³⁺/Fe²⁺ :E° =0,77 V ; MnO₄^-/Mn²⁺ : E°=1,51 V

couple Fe³⁺/Fe²⁺ : 5Fe²⁺ =5 Fe³⁺+5e^-

couple MnO₄^-/Mn²⁺ : MnO₄^-+8H⁺ +5e^- =Mn²⁺ +4H₂O

MnO₄^-+8H⁺ +5Fe²⁺ =Mn²⁺ +4H₂O +5 Fe³⁺.

log K₃ =5*(1,51-0,77)/0,06 = 61,7 : K₃ = 5 10⁶¹.

Le titrage est-il pertinent ?

Le dosage est pertinent car les réactions mises en jeu ont des constantes élévées, réactions totales.

Pourquoi doit-on incliner l’erlenmeyer ?

Pour accélérer le depôt du solide Cu₂O.

Pourquoi faut-il s’assurer qu’après ajout de la liqueur de Fehling le surnageant reste bien bleu ?

Les ions cuivre II doivent être en excès et le glucose en défaut.

Comment détecter le point d’équivalence lors du titrage par la solution de permanganate ?

L'ion permanganate, le seu ion coloré ( violet) joue un double rôle : réactif et indicateur de fin de réaction.

Peut-on être sûr de la concentration de la solution de permanganate si elle a été préparée à l’avance ?

L'ion permanganate est capable d'oxyder l'eau : la solution doit être préparée depuis peu.

Expérimentalement, on trouve un volume V_e= 20 mL de permanganate de potassium versé à l’équivalence

En déduire la concentration de la solution de glucose en g.L^-1.

C₆H₁₂O₆ +5HO^- +2CuT₂^2-= C₆H₁₁O₇^- +Cu₂O(s)+ 4T^2- +3H₂O.

d'où n(glucose) = n(Cu₂O).

Cu₂O(s) + 2Fe³⁺ + 2H⁺ = 2Cu²⁺ + 2Fe²⁺ + H₂O.

d'où n(Fe²⁺)= 2n(Cu₂O) = 2n(glucose).

MnO₄^-+8H⁺ +5Fe²⁺ =Mn²⁺ +4H₂O +5 Fe³⁺.

n(Fe²⁺) = 5 n(MnO₄^-) ; d'où : n(glucose)= 2,5 n(MnO₄^-)

n(glucose)= 2,5*20 10^-3*0,02 = 0,001 mol de glucose dans 20 mL ou encore 0,05 mol/L

M(glucose) =180 g/mol ; 180*0,05 = 9 g/L.