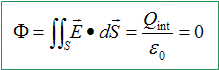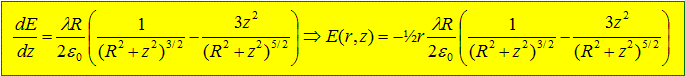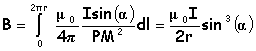champs électrostatique et magnétostatique d'un spire concours Mines 05 et 02

sans calculatrice.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

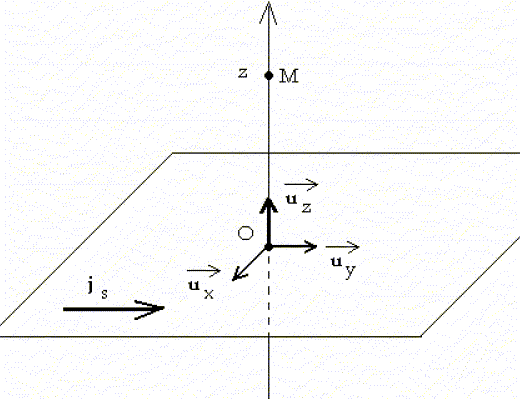
Champ magnétique crée par un plan.

Le plan infini P = (O, x, y) est parcouru par un courant électrique constant de densité surfacique j_S=j u_y. Soit M un point de l’axe (O, z) de cote z.

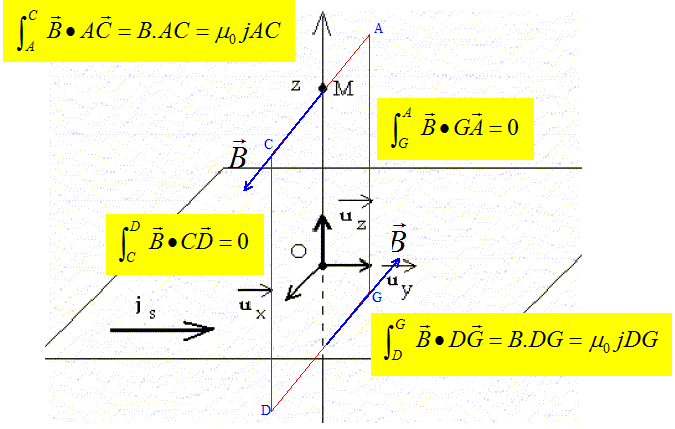
Donner, en la justifiant, l'expression vectorielle du champ magnétique B en M.

Le plan O u_y u_z , parallèle à j_S, est un plan de symétrie des courants: en conséquence, le champ magnétique B est perpendiculaire à ce plan : B =Bu_x.

Par translation suivant u_x, la distribution de courant est invariante ; par translation suivant u_y, la distribution de courant est invariante : donc la valeur du champ magnétique ne dépend que de z.

La règle de l'observateur d'Ampère donne le sens du champ magnétique : si z>0, B est dirigé suivant u_x ; si z<0, B est dirigé suivant -u_x.

Appliquer le thorème d'Ampère à la boucle ci-dessous :

La circulation de B sur la boucle ACDG vaut : 2B .AC = m₀jAC d'où B= ½m₀j.

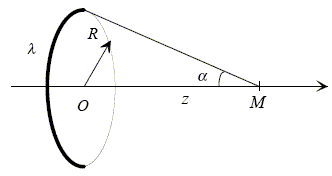
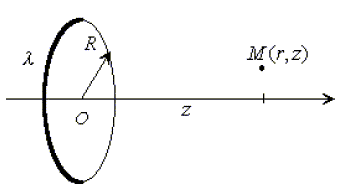
Montrer que ce champ présente une discontinuité à la traversée du plan et vérifier que cette discontinuité peut s'écrire : DB = B(z=0+)-B(z=0-) = m0jux. B(z=0+) = ½m0jux ; B(z=0-) = -½m0jux ; DB = ½m0jux + ½m0jux =m0jux

On admet que cette expression de la discontinuité est toujours valable à la traversée d'une membrane portant une densité surfacique de courant j, même si cette membrane n'est pas un plan infini. On considère un solénoide idéal, infini, parcouru par un courant constant d'intensite i, comportant n spires par mètre de longueur. On admet que le champ magnétique est nul à l'extérieur et uniforme à l'intérieur de la bobine.

Déduire de l'expression de la discontinuite ci-dessus la norme du champ magnetique à l'intérieur du solénoide, en fonction de n, m₀ et i.

champ extérieur : B_ext =0 ; champ intérieur, uniforme : B_int u_x;

discontinuité à la traversée de la membrane : m₀ j u_x

B_int u_x-B_ext =m₀ j u_x ; soit B_int u_x=m₀ j u_x.

La densité surfacique j est égale à l'intensité traversant une largeur d divisée par cette même largeur : j= n i d'où : B_int u_x=m₀ n i u_x.

On donne une spire circulaire de rayon R, de centre O, d'axe Oz. Cette spire porte une charge positive Q répartie uniformément avec une densité linéique de charge l en C.m^-1.

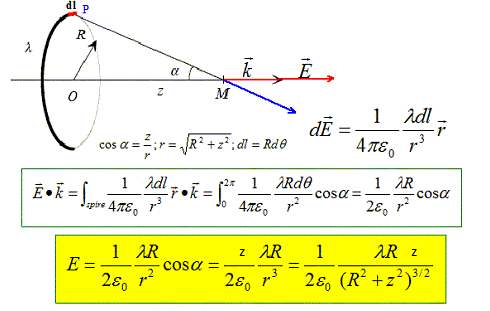
Montrer par des arguments de symétrie que, sur l'axe, le champ électrostatique E est porté par l'axe et prend la forme de E=Ek.

k est un vecteur unitaire porte par l'axe Oz.

 Tout plan défini par le point M et un diamètre de la spire ne modifie par la distribution de la charge :

E appartient à l'intersection de tous ces plans, c'est à dire que E est porté par l'axe Oz.

Dans une symétrie par raport au plan contenant la spire, z devient -z : donc E(-z) = -E(z).

Tracer le graphe de la fonction E(z).

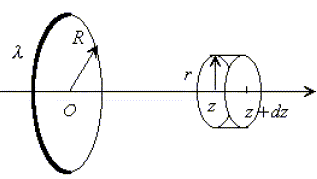
Champ au voisinage de l'axe.

On s'intéresse maintenant au champ électrostatique au voisinage de l'axe. On calcule donc le champ en un point M défini par des coordonnées cylindriques (r, q , z).

Montrer par des arguments de symétrie très précis, qu'en M, le champ E n'a pas de composante orthoradiale E_q .

Tout plan contenant l'axe Oz ne modifie par la distribution de la charge.

Pour r et z donnés, toute rotation autour de l'axe Oz ne modifie pas le champ E : E est indépendant de q.

Montrer qu'au voisinage de l'axe, le flux du champ E est conservatif. Que peut-on dire de sa circulation sur un contour fermé ?

A voisinage de l'axe, il n'y a pas de charge. Le théorème de Gauss conduit à :

Le champ E est à flux conservatif. Le champ E est à circulation conservative sur un contour fermé.

E(z+dz) pr²- E(z) pr²+ 2prdz E(r,z)=0

E(r,z)= -½ r [E(z+dz)-E(z)] / dz = -½r dE(z) / dz.

Calculer l'expression de E_r(z,r).

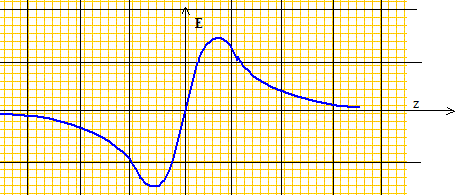
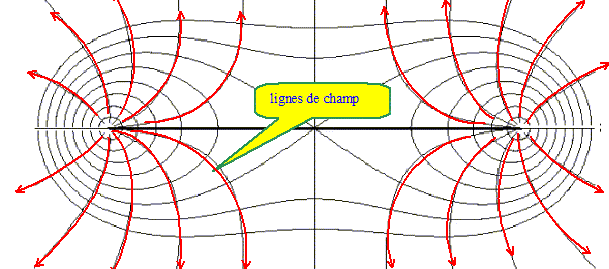
A l'aide d'un logiciel de simulation, on trace les lignes de champ et les équipotentielles.

Sur la feuille donnée en annexe, préciser les lignes de champ avec des flèches en supposant l > 0.

Qu'obtiendrait-on comme allure de lignes de champ à grande distance ?

La spire est alors équivalente à une charge ponctuelle située en son centre O et les lignes de champ sont des droites passant par O.

Qu'obtiendrait-on comme allure d'équipotentielles à grande distance ?

Des sphères centrées sur O.

Montrer que les lignes de champs sont perpendiculaires aux équipotentielles. Que se passe-t-il au centre ?

"équipotentielle" signifie potentiel V constant soit dV=0 et en conséquence E. dl=0

Le champ E est donc orthogonal aux équipotentielles.

Le champ est nul au centre.

Champ sur l'axe :

On donne une spire circulaire de rayon r , de centre O, d'axe Oz . Cette spire est parcourue par un courant électrique d'intensité I constante.

Montrer par des arguments de symétrie que, sur l'axe, le champ magnétostatique B est porté par l'axe et prend la forme de B=Bk.

k est un vecteur unitaire porte par l'axe Oz.

tout plan contenant l'axe de la spire est plan d'antisymétrie.

système invariant par rotation autour de l'axe : B est porté par l'axe Oz.

La règle de l'observateur d'Ampère donne le sens du champ magnétique B.

Calculer le champ magnétostatique créé en un point M de l'axe tel que OM = z . On écrira B(z) = B₀ f(z/r) où B₀ =B(O)

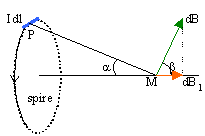
l'élément de courant Idl crée en M , le champ élémentaire dB, perpendiculaire à PM, de module :

Idl et PM étant perpendiculaire sin(q)=1

Par raison de symétrie le champ résultant sera porté par l'axe horizontal. La composante utile sera dBcos(b) = dBsin(a)

Pour tous les éléments Idl, l'angle a et PM sont les mêmes. L'intégration de dB sur toute la spire donne le module du champ résultant ( sin a = rayon r / PM )

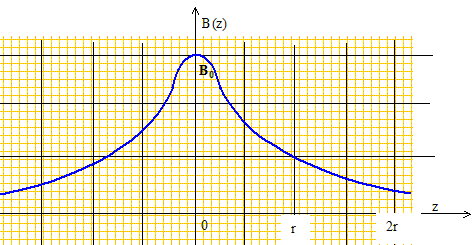
Au centre de la spire a=90°et sin a =1 d'où B₀ =m₀I/(2r).

cotan a = z/r ; 1+cotan²a= 1/sin²a ; sina = 1/(1+cotan²a)^½ =[1+(z/r)²]^-½

par suite B=B₀[1+(z/r)²]^-3/2

Tracer le graphe représentant les variations de la fonction B(z).

Champ au voisinage de l'axe.

On s'intéresse maintenant au champ électromagnétique au voisinage de l'axe. On calcule donc le champ en un point M défini par des coordonnées cylindriques (r, q , z).

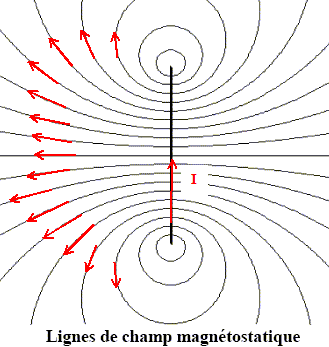
Montrer par des arguments de symétrie très précis, qu'en M, le champ B n'a pas de composante orthoradiale B_q .

tout plan contenant l'axe Oz de la spire est plan d'antisymétrie : B appartient à ce plan, donc B_q=0.

Pour r et z donnés, le système est invariant par rotation autour de l'axe : B ne dépend pas de q.

Compléter sur la feuille les lignes de champ par des flèches en indiquant leur sens, en précisant le sens du courant.

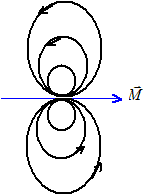
Qu'obtiendrait-on comme allure de lignes de champ à grande distance ?

La spire est assimilable à un dipole électromagnétique.

Quelle(s) différence(s) fondamentale(s) a-t-on entre les deux topographies ?

Les lignes de champ électrostatique divergent à partir des charges ; les lignes de champ électromagnétique tournent autour des courants.

Montrer qu'au voisinage de l'axe, la circulation de B est conservative.

Il n'y a pas de courant au voisinage de l'axe : la circulation de B est conservative.

Que peut-on dire du flux de B à travers une surface fermée ?

Le flux de B est toujours conservatif.

Calculer explicitement B (z, r) . B(r,z)= -½r dB(z) / dz.

B=B₀[1+(z/R)²]^-3/2 ; dB(z)/dz = -3z B₀ /r²[1+(z/R)²]^-5/2

B(r,z)= 3rz B₀ /(2R²)[1+(z/r)²]^-5/2.