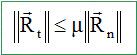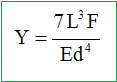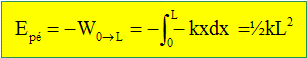propriétés mécanique d'un verre : coefficient de frottement, modèle d'élasticité concours Mines 04

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

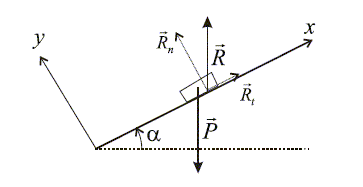
Coefficient de frottement :

On se propose de mesurer le coefficient de frottement du verre sur le verre, note m. Pour cela, on dispose d'une grande vitre plane et d'un petit morceau de verre parallèlépipédique de masse m. On pose le petit morceau de verre sur la vitre initialement horizontale et on incline doucement la vitre. On notera a l'angle que fait la vitre avec l'horizontale.

Le coefficient de frottement m est défini comme suit : tant que le morceau de verre ne glisse pas sur la vitre, la norme de la composante tangentielle de la réaction du support est inférieure à m fois la norme de la composante normale de la reaction :

En supposant que le petit morceau de verre soit immobile,

exprimer les composantes normale et tangentielle de la réaction en fonction de la masse m du petit morceau de verre, de l'accélération de la pesanteur g et de l'angle a.

A l'équilibre le poids du morceau de verre est opposée l'action du plan : mg = R

R_t = mg sin a ; R_n = mg cos a.

En déduire une condition sur l'angle a et sur le coefficient de frottement m pour que le petit morceau de verre ne glisse pas.

R_t <= mR_n ; sin a<= mcos a ; tan a<= m.

Expérimentalement, on remarque que pour a >= 35° le petit morceau de verre se met à glisser.

En déduire la valeur de m.

m = tan 35 = 0,70.

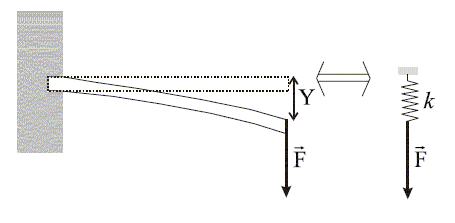
Le verre est un matériau très dur. On peut toutefois le déformer légèrement sans le casser : on parle d'élasticité. Récemment, des expériences de biophysique ont été menées pour étudier l'ADN. Le capteur utilisé était simplement une fibre optique en silice amincié à l'extremité de laquelle on accroche un brin d'ADN. L'expérience consistait à suivre la déformation de flexion de la fibre. La masse volumique du verre est r= 2500 kg.m^-3.

La fibre de verre de longueur L et de diamètre d est encastrée horizontalement dans une paroi immobile. Au repos, la fibre est horizontale (on néglige son poids). Quand on applique une force verticale F (on supposera que la force F reste verticale tout au long de l'expérience) à l'extremité libre de la fibre, celle-ci est deformée. L'extremité est déplacée verticalement d'une distance Y que l'on appelle la flêche.

La flèche Y est donnée par la relation suivante (on notera la présence du facteur numérique 7, sans dimension, qui est en fait une valeur approchée pour plus de simplicité) :

où E est le module d’Young du verre. Pour les applications numériques on prendra pour le module d’Young E=7.10¹⁰ SI.

Quelle est l’unité SI du module d’Young E ?

E = 7L³F/(Yd⁴).

7 est sans dimension ; Y et d sont des longueurs : [Yd⁴]= L⁵ ; L est une longueur : [L³]=L³ ;

F est une force , une masse fois une ccélération :[F] = MLT^-2 ;

d'où [E] =L³ MLT^-2 L^-5 =M L^-1T^-2.

En considérant uniquement la force F, montrer que l’on peut modéliser la fibre de verre par un ressort de longueur à vide nulle et de constante de raideur k dont on donnera l’expression analytique en fonction de E, d et L. donne : F =YEd4/(7L3) = k( Y-0) avec k = Ed4/(7L3).

Calculer numériquement k pour une fibre de longueur L= 7 mm et de diamètre d = 10 mm.

k = 7.10¹⁰ (10^-5)⁴ / (7*(7 10^-3)³)) = 2,9 10^-4 N m^-1.

Démontrer l’expression de l’énergie potentielle élastique d’un ressort de longueur à vide nulle, de constante de raideur k, lorsque sa longueur est L.

L'énergie potentielle élastique est l'opposée du travail de la force de rappel -kx avec x= L-L₀. ( ici L₀=0)

En reprenant l’analogie du ressort, quelle est alors l’énergie potentielle élastique de la fibre de verre lorsque la flèche vaut Y ?

On donnera la relation en fonction de E, d et L.

E_pé = ½k Y² = Ed⁴/(14L³)Y².

On a tous fait l'expérience suivante : faire vibrer une règle ou une tige lorsque une de ses extrémités est bloquée. On cherche ici à chercher les grandeurs pertinentes qui fixent la fréquence des vibrations. L'extrémité de la tige vaut Y(t) à l'instant t. On admet que lors des vibrations de la fibre, l'énergie cinétique de la fibre de verre est donnée par l'expression :

E_c =rLd² [dY/dt]².

Ecrire l’expression de l’énergie mécanique de la fibre en négligeant l’énergie potentielle de pesanteur.

L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle :

E_M= Ed⁴/(14L³)Y² + rLd² [dY/dt]².

Justifier que l’énergie mécanique se conserve au cours du temps. En déduire l’équation différentielle qui régit les vibrations de la fibre.

En absence de force non conservative (frottement par exemple) , l'énergie mécanique se conserve.

Dériver l'expression de l'énergie mécanique par rapport au temps :

0 =2Ed⁴/(14L³) Y .dY/dt + 2rLd² [dY/dt] d²Y/dt².

Simplifier par 2d²dY/dt :

0 =Ed²/(14L³) Y + rL d²Y/dt².

0 =Ed²/(14rL⁴) Y + d²Y/dt².

Quelle est l’expression de la fréquence propre de vibration d’une tige de verre de module d’Young E, de longueur L et de diamètre d.

pulsation w₀² = Ed²/(14rL⁴) ; w₀ =d/L² [E/(14r]^½ ; fréquence f₀ =w₀ /(2p)

f₀ =d [E/(14r]^½ /(2pL²).

Calculer numériquement la fréquence des vibrations d'une fibre de verre de longueur 7 mm et diamètre 10 mm.

f₀ = 10^-5 [7.10¹⁰ / (14*2500)]^½ / (6,28*49 10^-6)

f₀ = 46 Hz.