Pompe à chaleur : diagramme entropique, chauffage d'une piscine. concours Mines 03

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

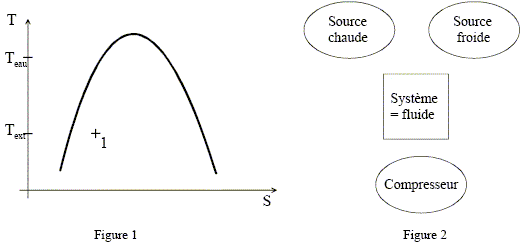
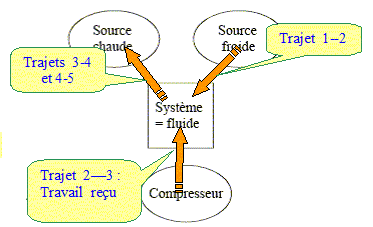
Une pompe à chaleur permet de maintenir constante la température de l'eau de la piscine ; on se placera donc en régime permanent. La machine thermique fonctionne avec deux sources de chaleur (thermostats) : l'air extérieur de température T_ext et l'eau de la piscine de température T_eau.

Le fonctionnement de la pompe à chaleur est basé sur le cycle d'un fluide caloporteur ayant une température d'ébullition basse. Le fluide caloporteur, initialement sous forme d’un mélange liquide-vapeur au point 1, traverse l'évaporateur où l'air extérieur lui permet de subir une vaporisation complète (trajet 1-2). Le compresseur comprime ensuite cette vapeur (trajet 2-3), augmentant ainsi sa température ; on supposera cette transformation isentropique. Au niveau du condenseur, la vapeur surchauffée voit d'abord sa température descendre jusqu'à T_eau en suivant une transformation isobare (trajet 3-4). Le fluide caloporteur,

toujours comprimé, redevient ensuite liquide (trajet 4-5). La soupape de détente réduit la pression du fluide caloporteur (trajet 5-1), transformation au cours de laquelle la température du fluide s'abaisse fortement le rendant prêt pour un nouveau cycle.

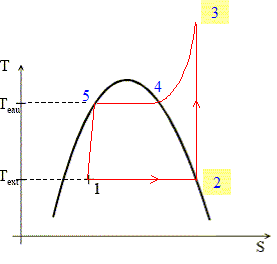
Pour un point i (compris entre 1 et 5) du cycle, on note P_i, T_i et V_i la pression, la température et le volume du fluide caloporteur.

Calculer la variation d’entropie DS de la vapeur assimilée à un gaz parfait pour une transformation isobare entre les températures T₃ et T₄.

L'entropie est une fonction d'état. Sa variation ne dépend que de l'état final et de l'état initial. On imagine une transformation réversible allant de l'état 3 à l'état 4.

Variation élémentaire d'entropie : dS = C_p dT / T avec C_p indépendant de la température.

dS= C_p d ln T.

Puis intégrer de T₃ à T₄ : DS= C_p ln (T₄ /T₃ ).

Le dessin de la figure 1 donne l'allure de la courbe d'équilibre liquide-vapeur du fluide considéré dans le diagramme (T,S). On y a repéré le point 1 correspondant au début du cycle. Reproduire le schéma sur votre feuille et placer les points 2, 3, 4 et 5.

Pour chaque trajet (sauf le trajet 5-1), justifier rapidement l’allure des courbes ainsi obtenues.

Trajet 1-2 : la vaporisation s'effectue à pression et température constante : droite horizontale.

Le liquide est entièrement vaporisé.

Trajet 2--3 :compression isentropique : droite verticale.

Trajet 3--4 :   isobare d'un gaz DS=S₄-S₃ = C_p ln (T₄/T₃). La température de la vapeur diminue jusu'à T_eau.

Trajet 4--5 : la vapeur se condense à température constante.( droite horizontale )

Trajet 5--1 : refroidissement du liquide.

Reproduire le diagramme de la figure 2 et indiquer par des flèches les sens réels des flux thermiques et du travail. Indiquer dans quelles étapes du cycle ces flux ont lieu.

Quel est l'intérêt, pour une pompe à chaleur, d’utiliser un changement d’état ?

Un liquide peut emmagasiner plus d'énergie qu'un gaz : la vapeur libère beaucoup plus d'énergie en se condensant qu'en se refoidissant.

Quel est l'intérêt d'utiliser un fluide caloporteur de température d'ébullition basse ?

La température de vaporisation du fluide doit être comprise entre la température de la source froide et celle de la source chaude.

Donner la définition de l'efficacité thermodynamique h de la pompe à chaleur. Energie cédée à la source chaude / travail investi. h = -Qchaude / W. Montrer que l'efficacité réelle de toute pompe à chaleur est inférieure à l’efficacité hc obtenue dans le cas d’un fonctionnement réversible. On a ici h = 5 Le premier principe s'écrit sur le cycle : DU=0 = W+Qfroide+Qchaude(1). Second principe : Qfroide/ Tfroide +Qchaude/ Tchaude <=0 (2). (1) donne : W= -Qfroide-Qchaude. h = -Qchaude / W = Qchaude / (Qfroide+Qchaude) h =1/ [Qfroide/ Qchaude+1 ] (2) donne : Qfroide/ Qchaude<= -Tfroide/ Tchaude . h <=1/ [1-Tfroide/ Tchaude ]. L'égalité correspond à la réversibilité.

Les pertes de la piscine sont essentiellement dues à l'évaporation de l'eau dans l'air. Dans les conditions précisées plus haut, le taux d'évaporation par heure et par mètre carré de surface d'eau est de a = 150 g.h^-1.m^-2.

En déduire l'énergie perdue pendant une heure par l'eau de la piscine.

Données : surface de la piscine : S= 250 m². C_eau = 4,18 J g^-1 K^-1 ; T_ext = 283 K ; T_eau = 299 K; L_vap =2800 J g^-1.

Masse d'eau évaporée par heure par une surface de 250 m² :

m = 250*150 =3,75 10⁴ g.

Energie perdue par cette eau : E= m L_v = 3,75 10⁴ *2800 =1,05 10⁸ J.

Quel doit être le travail que l'on doit fournir au fluide pour que la pompe à chaleur puisse maintenir la température de la piscine constante pendant une heure ?

h = 5 = -Q_chaude / W d'où W = 5*(-Q_chaude) = 1,05 10⁸ / 5 = 2,1 10⁷ J.

Comparer ce travail à l'énergie qu'il aurait fallu fournir si on chauffait l'eau de la piscine avec une simple résistance électrique.

L'énergie électrique doit compenser l'énergie perdue par l'eau de la piscine, soit : 1,05 10⁸ J, cinq fois plus grand que dans le cas de la pompe à chaleur.

Une pompe permet de faire circuler l'eau de la piscine à travers des panneaux solaires (simples tuyaux noirs) placés sur le toit du bâtiment. L'énergie solaire réchauffe l'eau des panneaux qui retourne ensuite dans la piscine.

Soit S' = 100 m² la surface des panneaux solaires.

Déterminer l'énergie reçue par l'eau de la piscine pendant une heure en supposant que l'éclairement moyen reçu au niveau des panneaux solaires est de 300 W/m² et que toute l'énergie solaire y est absorbée.

Puissance solaire reçue par 100 m² de panneaux :

300*100 = 3 10⁴ W.

Energie reçue pendant 1 h = 3600 s :

3 10⁴ *3600 = 1,08 10⁸ J.