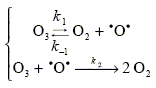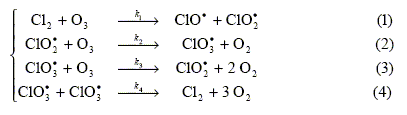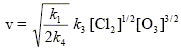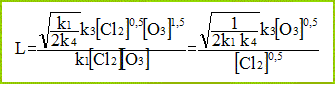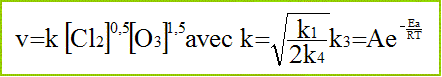|
cinétique chimique : décomposition de l'ozone atmosphérique concours Mines 03 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
Le but de cette partie est d’étudier le mécanisme de la décomposition de l’ozone, et l’influence des chlorofluorocarbures (C.F.C.) sur cette décomposition (qui mène au problème actuel du « trou » dans la couche d’ozone). L’ozone est thermodynamiquement instable par rapport au dioxygène. Il peut se décomposer, en l’absence de catalyseur, suivant la réaction très lente : 2 O3(g)--> 3 O2(g) pour laquelle on peut proposer le mécanisme suivant :
Rappeler la définition d’un intermédiaire réactionnel. Illustrez votre définition d’un exemple tiré du mécanisme précédent. Espèce formé au cours d'une étape et qui est consommée lors d'une étape ultérieure : un intermédiaire réactionnel ne figure pas dans le bilan de la réaction. Les intermédiaires réactionnels restent en quantité pratiquement constante et très faible. d[Pintermédiaire] / dt =0 exemple tiré de ce mécanisme : .O.. Déterminer la loi de vitesse de la réaction précédente en fonction de [O3], [O2] et des constantes de vitesse. On appliquera pour cela le principe de Bodenstein, ou des états quasistationnaires. 2 O3(g)--> 3 O2(g) ; v = 1/3 d[O2]/dt. d[O2]/dt = k1[O3]-k-1[O2][.O.] + 2k2 [O3][.O.] (1) d[.O.]/dt = k1[O3]-k-1[O2][.O.]-k2 [O3][.O.]=0 (2) (1)- (2) donne : d[O2]/dt =3k2 [O3][.O.] (3) (2) donne [.O.] = k1[O3] / ( k-1[O2] + k2 [O3] ) Repport dans (3) : d[O2]/dt = 3 k1 k2 [O3]2 / ( k-1[O2] + k2 [O3] ). v = k1 k2 [O3]2 / ( k-1[O2] + k2 [O3] ).
Justifier cette
affirmation. Un inhibiteur est une substance chimique
ralentissant ou empêchant une réaction
. Dans l'expression de v,
[O2] figure au
dénominateur : si la concentration en
dioxygène croît, alors la vitesse v
diminue. destruction de l’ozone atmosphérique. En effet, la vitesse de décomposition de l’ozone est fortement accrue en présence de dichlore. Le mécanisme proposé est le mécanisme de réaction en chaîne suivant :
Rappeler les différentes étapes, ainsi que leur signification, que comporte un mécanisme de réaction en chaîne. Identifiez-les dans le mécanisme ici proposé. Initiation : étape 1, création d'intermédiaires réactionnels. Propagation : étapes 2 et 3, consommation puis régénération de ces intermédiaires. Terminaison : étape 4, disparition des intermédiaires réactionnels.
Justifier alors le rôle catalytique du dichlore dans la décomposition de l’ozone. Dans l'expression de v, [Cl2] figure au numérateur : si la concentration en dichlore croît, alors la vitesse v augmente. Le dichlore se comporte donc comme un catalyseur.
On définit la longueur moyenne de chaîne, notée L , par : L = vitesse globale de décomposition de O3 / vitesse d'initiation. Déterminer l’expression de L en fonction de [O3], [Cl2] et des ki (i = 1, 2, 3 ou 4). L'étape (1) est l'initiation ; la vitesse de cette réaction est : k1[Cl2] [O3].
Quelle est l’influence de [Cl2] sur cette longueur de chaîne ? L est inversement proportionnelle à la racine carrée de la concentration en dichlore. Si [Cl2] croît, alors la longueur de chaîne diminue.
Montrer que la réaction globale obéit à la loi d’Arrhénius. La vitesse peut se mettre sous la forme :
En déduire l’expression de son énergie d’activation en fonction des énergies d’activation des différentes étapes. k1 = A1 exp (-Ea1/(RT)) ; k3 = A3 exp (-Ea3/(RT)); k4 = A4 exp (-Ea4/(RT)) ; k= A exp(-Ea/(RT)). On identifie : exp(-Ea/(RT)) à exp (-½Ea1/(RT)) . exp (-Ea3/(RT)) . exp (+½Ea4/(RT)) soit Ea = ½Ea1+Ea3-½Ea4.
|
|||||||
|
|
|||||||
|
|