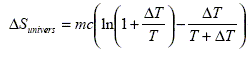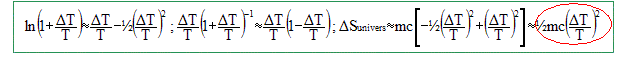|
Etude de quelques phénomènes irréversibles concours Mines 03 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
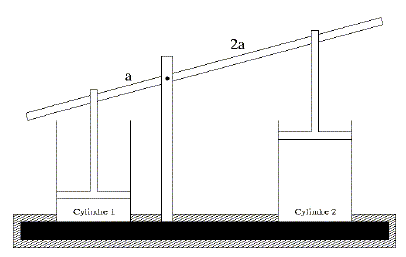
Une transformation réversible doit être très lente ; les frottements doivent être nuls. La transformation réversible peut être considérée comme une succession d'états d'équilibre. Si on inverse le sens de la contrainte extérieur responsable de la transformation, on repasse par les mêmes états d'équilibre. Donner deux exemples de phénomènes à l’origine de l’irréversibilité d’une transformation. Les frottements mécaniques, les différences de pression, de température ou de concentrations. Illustration du principe d’entropie maximale. Deux cylindres de même section S, contenant deux gaz qui peuvent être différents, sont fermés par deux pistons étanches. Ces deux pistons sont solidaires en ce sens que leurs axes restent verticaux et sont attachés aux bras d’un levier dont le point fixe est deux fois plus près du premier cylindre que du second. Les deux cylindres reposent sur une table qui conduit la chaleur (une table métallique) et a pour seul effet de permettre les échanges de chaleur entre les deux systèmes, c’est-à-dire entre les gaz contenus dans les deux cylindres. Le système complet formé par ces deux cylindres est isolé et n’est pas soumis à une pression extérieure. Les capacités thermiques des cylindres et de la table sont négligeables.
Déterminer la relation imposée par la présence du levier sur les variations de volumes dV1 et dV2 des deux cylindres. Si le cylindre 1 se déplace d'une valeur dz vers le haut, alors le cylindre 2 se déplace d'une valeur 2dz, vers le bas ( théorème de Thalès). Les cylindres ayant même section, si le volume du cylindre 1 augmente de dV1, alors le volume du cylindre 2 diminue de dV2 = 2 dV1. dV2 = -2 dV1. Écrire l’expression de la variation infinitésimale dS du système complet formé par les deux cylindres en fonction des températures T1 et T2 des gaz contenus dans les deux cylindres, des pressions P1 et P2 qui règnent dans les deux cylindres et des seules variations dV1 (variation de volume du gaz contenu dans le cylindre 1) et dU1 (variation de l’énergie interne du gaz contenu dans le cylindre 1). " Le système complet formé par ces deux cylindres est isolé et n’est pas soumis à une pression extérieure." L'énergie interne de l'ensemble est donc constante : dU = dU1+dU2=0 ; dU1= -dU2. à l'équilibre, quelles que soient les variations dU1 et dV1, dS=0. En déduire la relation entre les températures T1 et T2, puis celle entre les pressions P1 et P2 des gaz dans les cylindres 1 et 2 lorsque l’équilibre est atteint. La relation (1) conduit à l'égalité des températures ( T1=T2) et à : P1=2P2.
Quantité d'énergie gagnée par le solide s'échauffant de T1 à T1+dT : dQ= m c dT L'entropie est une fonction d'état ; on imagine une transformation réversible permettant de passer de l'état 1 à l'état 2. variation d'entropie correspondante du solide : dS= dQ/T = m c dT/T = m c d ln T. Intégrer de T1 à T2 : DSsolide = m c ln(T2/T1). DSsolide = 10 ln (373/273) =3,12 = 3,1 J K-1.
Le thermostat constitue un système réversible dont la température est constante, égale à T2. Energie cédée par le thermostat au solide : -mc(T2 -T1) variation d'entropie correspondante : DSeau = -mc(T2 -T1)/T2. DSeau = -10*100/373 = -2,68 = -2,7 J K-1. En déduire la variation de l’entropie de l’univers D Sunivers, constitué par l’ensemble {solide + thermostat}, lors de ce processus ; puis faites l’application numérique. D Sunivers = DSeau + DSsolide = 3,12-2,68 = 0,44 J K-1. Commentez votre résultat. D Sunivers >0 : la transformation de ce système isolée est irréversible. On découpe le processus précédent en une infinité de petits processus au cours desquels on élève la température du solide de T à T + DT (avec D T << T) par contact avec une infinité de thermostats de températures infiniment proches les unes des autres. Montrer que, pour une étape intermédiaire, on peut écrire :
Dans les expressions ci-dessus, il suffit de remplacer T1 par T et T2 par T+DT : d'où DSsolide = m c ln[( T+DT) / T] ; DSeau = - m cDT / ( T+DT)
En développant ce résultat au deuxième ordre en DT/T, montrer que DSunivers est proportionnelle à [DT/T]2.
En déduire que ce processus peut être rendu réversible à la limite où la variation de température DT entre deux thermostats successifs tend vers zéro. Si DT tend vers zéro, DSunivers tend vers zéro : la transformation tend vers une transformation réversible.
|
|||||||
|
|
|||||||
|
|
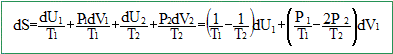 (1)
(1)