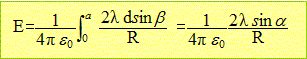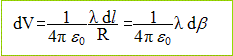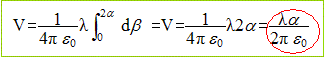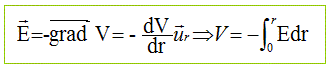|
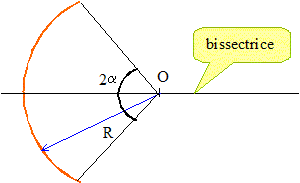
champ et potentiel électrique crée en son centre par un arc de cercle ; crée en un point M par un cylindre uniformément chargé en surface. En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
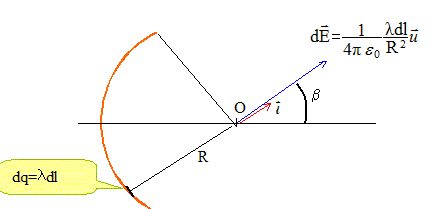
Champ crée en O par un élément de longueur dl portant la charge dq=ldl.
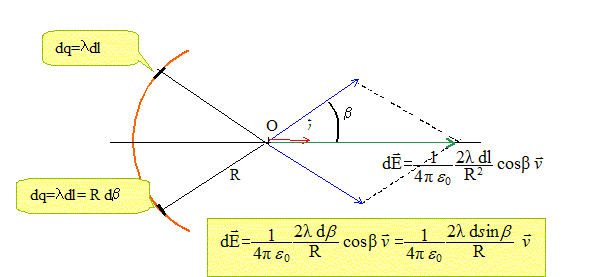
Champ crée en O par deux éléments de longueur dl portant la charge dq=ldl, symétrique par rapport à la bissectrice.
Intégrer entre 0 et a :
Intégrer entre 0 et 2a :
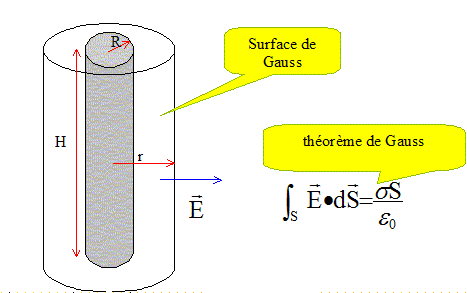
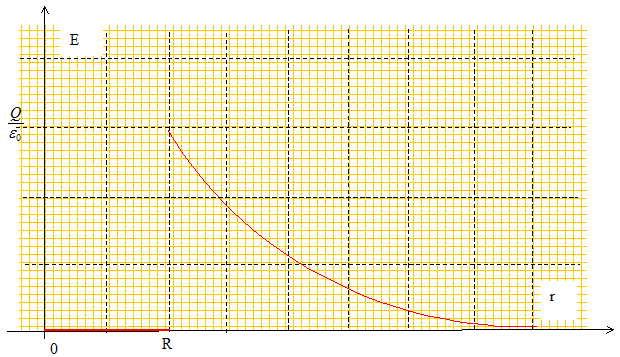
Champ électrique crée par un cylindre infini portant la charge surfacique s. Le champ électrique, en un point M d'un plan de symétrie du système de charges, appartient à ce même plan de symétrie. Tout plan contenant l'axe du cylindre est plan de symétrie et tout plan perpendiculaire à l'axe du cylindre est également plan de symétrie (cylindre infini) donc le champ est radial.
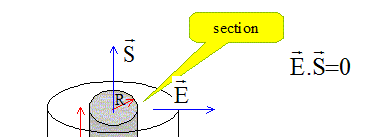
Le flux du champ électrique à travers les deux sections est nul ( champ perpendiculaire à la surface).
Flux du champ électrique à travers la surface latérale : Slat = 2pr H Charge totale contenue dans cette surface : Q = s 2pR H. Appliquer le théorème de Gauss : r > R : E 2pr H = s 2pR H / e0. E = s R / (re0). r<R : E 2pr H =0 ; E=0.
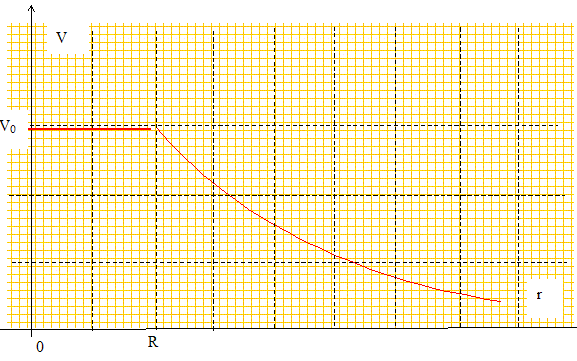
Potentiel : On considère que le potentiel V est égal à V0 sur l'axe du cylindre.
r <R : E=0 ; V=V0. r>R, E = s R / (re0) ; V= -s R /e0 ln r + Cte Comment trouver la constante d'intégration ? Lors de la traversée de la surface du cylindre de rayon R, V est continu. V(r=R) = V0 = -s R /e0 ln R + Cte d'où Cte = V0 +s R /e0 ln R V= V0 -s R /e0 ln(r/R).
|
|||||||
|
|
|||||||
|
|