électron dans un champ électrique, circuit inductif. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

circuit inductif. Un circuit est constitué par une bobine d'induction propre(self-induction) L en série avec une résistance R dont une fraction est initialement court-circuitée : la résistance initiale n' est que r. Il est alimenté par une source de tension E de résistance interne négligeable. Loi d'évolution du courant après l'ouverture de l'interrupteur. additivité des tensions : uL+uR= 0 avec uR= Ri. uL = L di dt Equation différentielle régissant l'intensité : L di dt +R i=0 Solution de cette équation différentielle : i(t) =A exp(-t/t) avec t = L/R, constante de temps Lorsque le régime permanent est établi , l'intensité est constante, égale à I = E/R ; A la date de l'ouverture i(0) = I = E/R d'où : i(t) =E/R exp(-t/t). Différence de potentiel aux bornes de l'interrupteur au moment de l'ouverture. Ouverture de l'interrupteur : Continiuité de l'intensité à la date de l'ouverture de l'interrupteur K : uR (0) = RI = E Discontinuité de la tension aux bornes de la bobine : uL(0) =L [di/dt ]t=0= -E. Additivité des tensions : E = uL(0)+ uR(0) + uK (0) d'où uK (0) = E à la date de l'ouverture de l'interrupteur. 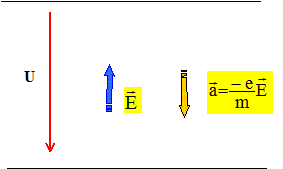temps de transit : Calcul du temps de transit d'un électron de la cathode à l'anode d'une diode dont les électrodes sont supposées planes et parallèles (on négligera la vitesse initiale et les effets relativistes)   La différence de potentiel de l'anode à la cathode est U=50 volts.La distance athode-anode d=1 mm = 10-3 m. La charge massique de l'électron e/m=1,76 1011 C kg-1. L'électron étant placé dans un champ électrique E est soumis à une force électrique de valeur F= e E. Le poids des électrons est négligeable devant la force électrique. Ecrire la deuxième loi de newton, d'où la valeur de l'accélération de l'électron : a = e/m E ; avec E = U/d d'où a : a = eU md = 1,76 1011*50 10-3 = 8,8 1015 m s-2. Le mouvement de l'électron est rectiligne uniformément accéléré avec une vitesse initiale nulle: La distance d est parcourue pendant la durée t telle que : d = ½at2 ; t = (2d)½ a½ = (2 10-3)½ (8,8 1015)½ = 4,8 10-10 s. Calcul du temps de transit d'un électron de la cathode à l'anode à l'écran fluorescent d'un tube des oscilloscopes : - en tenant compte des effets relativistes : EC=mc2[g-1 ] avec g = (1-v2/c2)-1. Donnés : U=25 kV = 2,5 104 V ; distance anode cathode d=25cm = 0,25 m Accélération : a = eU md = 1,76 1011*2,5 104 0,25 = 1,76 1016 m s-2. Or a = Dv/Dt = v / Dt ( la vitesse initiale étant nulle) d'où la durée : Dt = v/a. Vitesse finale v : DEC = eU; l'énergie cinétique initiale étant nulle, il vient : mc2[g-1 ] = eU. g-1 = eU mc2 = 1,76 1011*2,5 104 (3 108)2 = 4,89 10-2. g = 1,0489 ; or g = (1-v2/c2)-1 d'où (1-v2/c2) = 1/1,0489 =0,953 v2/c2 = 1-0,953 =4,66 10-2 ; v =6,48 107 m/s. Par suite D t = 6,48 107 / 1,76 1016 =3,7 10-9 s. Ordonnée du point d'impact sur un écran. Aux armatures d'un condensateur plan, on applique une différence de potentiel de 2,5 V. La distance entre les armatures est de 2 cm et la longueur des plaques 5 cm. Déterminer la trajectoire d'un électron d'énergie initiale 30 électron-volt après avoir traversé, en largeur, le condensateur. Vitesse initiale v0 de l'électron : 30 eV = 30*1,6 10-19 =4,8 10-18 J. ½mv02 = 4,8 10-18 avec m = 9,1 10-31 kg. v02 = 2* 4,8 10-18 / 9,1 10-31 =1,05 1013 ; v0 = 3,25 106 m/s. 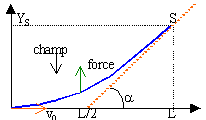Le poids de l'électron est négligeable devant la force électrique. au départ: accélération ( 0; eE/m) ; vitesse ( v0 ; 0) ; vecteur position nul. à la date t vitesse (v0 ; eEt/m) position(x=v0t; y=½eEt2/m) ; y = eEx2 2mv02 branche de parabole Déterminer notamment le point d'impact sur un écran placé à 50 cm au-delà du condensateur. Ordonnée du point S d'abscisse L : yS = eEL2 2mv02 E = U/d = 2,5/0,02 = 125 V m-1 ; L = 0,05 m ; e/m = 1,76 1011C kg-1. yS = 1,76 1011 *125*0,052 2*1,05 1013 = 2,62 10-3 m Calcul de l'angle a : tan a= yS 0,5 L = 2,62 10-3 2,5 10-2 = 0,105 Point d'impact Y sur l'écran situé à D=0,5 m de la sortie du condensateur : tan a= Y D ; Y =D tan a =0,5*0,105 = 5,2 10-2 m

retour -menu