une histoire du microscope ; concours ITPE 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

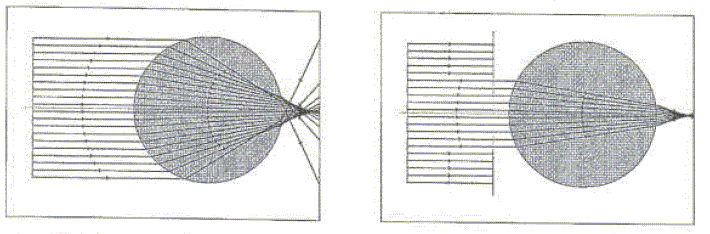
du grec mikros, petit et skopein, examiner. Microscope de Van Leeuwenhoek 1610. Bille sphérique insérée entre deux plaques de cuivre, elle grossit de 50 à 300 fois. Leuwenhoek semle même avoir été le premier à décrire les spermatozoïdes et les protozoaires sans qu'il se soit douté de leur fonction. On étudie les propriétés d'une bille sphérique de verre de rayon R et d'indice n. On s'en sert comme d'une loupe pour faire converger les rayons solaires. Définir le mot stigmatisme.  Tout faisceau incident, issu d'un point lumineux, donne un rayon émergent du système optique, convergent en un point unique. La bille est-elle stigmastique ? Justifier.  La bille n'est pas stigmatique : le faisceau incident est constitué de rayons parallèles. Le faisceau émergent ne converge pas en un point unique. Commenter le second schéma.  Le faisceau incident est diaphragmé : on élimine les rayons trop éloignés de l'axe optique. Le faisceau émergent converge en un point unique : on se place dans les conditions de Gauss. Rappeler la loi de la réfraction de Snell-Descartes. 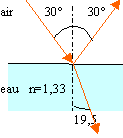Rayons incident, réfléchi et réfracté sont dans le même plan. réflexion : angle d'incidence = angle de réflexion =30° réfraction : nair sin 30 = n eau * sin i2 sin i2 = 1*0,5 / 1,33 i2 = 19,5°   Démontrer que i = i'. Dioptre d'entrée : nair sin i = nverre sin r Dioptre de sortie nverre sin r = nair sin i' en conséquence i = i'.     Déterminer uniquement en fonction de i et de r les angles (PC, PF) et (FC, FP). angle (PC, PF) = p-i' = p-i. i + (p-2r) + angle (CP, CF) = p ; angle (CP, CF) = 2r-i triangle CPF : angle (CP, CF) + angle (FC, FP) + p-i = p. 2r-i + angle (FC, FP) + p-i = p ; angle (FC, FP) =2(i-r). Dans le cadre de l'approximation des petits angles, déterminer l'expression de CF en fonction uniquement de n et R. rappel : dans le triangle CPF : sin(PC, PF) / CF = sin(FC, FP) / CP CF = CP sin(PC, PF) / sin(FC, FP) CF = R sin ( p-i) / sin (2(i-r)) ; or sin (p-i)= sin i = n sin r. Pour les petits angles, le sinus est assimilé à l'angle en radian : sin ( 2(i-r)) proche de 2(i-r) ; sin i = n sin r s'écrit i proche de n r. CF= R n sin r / sin (2(i-r) voisin de : Rn r / (2r(n-1) = Rn/(2(n-1)).   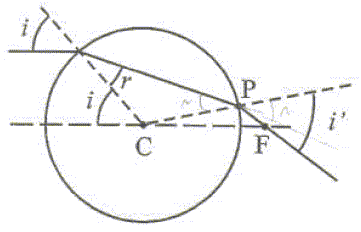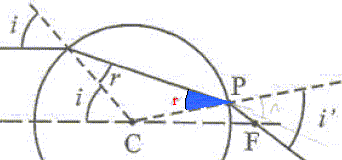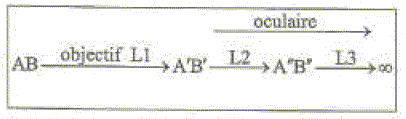Etude historique : R= 0,6 mm et n =1,5. L'objet à étudier est maintenu dans le plan focal F au sommet d'une tige dont on peut régler la hauteur par un système de vis. On observe alors son image fortement agrandie par rapport à la vision directe où on ne pourrait pas observer longuement l'objet à moins de d= 25 cm de l'oeil. Calculer la valeur CF de la focale. CF= Rn/(2(n-1))= 0,6*1,5 /1 = 0,9 mm. Quelle est la valeur numérique du grossissement G=d/CF de ce microscope.  G= 250 / 0,9 = 280. Quel est le gros défaut de ce microscope rudimentaire ? Au regard de la taille de ce dispositif, il reçoit peu de lumière et est pratiquement inutilisable. Principe du microscope moderne 1757 John Dolland On se propose de monter sur un banc d'optique un système de 3 lentilles fonctionnant comme un microscope sans pour autant en avoir les performances. On travaille dans les conditions de Gauss. Définir le mot emmétrope. Un oeil emmétrope est sans défaut Rappeler un ordre de grandeur du grossissement maximum d'un microscope optique. En pratique on ne dépasse pas un grossissement de 1000. La principale qualité d'un microscope est son pouvoir séparateur, et non son grossissement. Pourquoi ne peut-on pas monter sur le banc d'optique un ensemble de lentilles ayant le même grossissement qu'un microscope ? La longueur du banc est limitée à 2 m ; la hauteur de l'objet est de l'ordre du mm ; il faut rester dans les conditions de Gaus( utiliser un diaphragme)  L'objectif est représenté par la lentille convergente L1. l'oculaire est représenté par les deux lentilles convergentes L2 et L3. Les foyers objets des lentilles L1, L2 et L3 sont respectivement F1, F2 et F3. Les foyers images des lentilles L1, L2 et L3 sont respectivement F'1, F'2 et F'3. 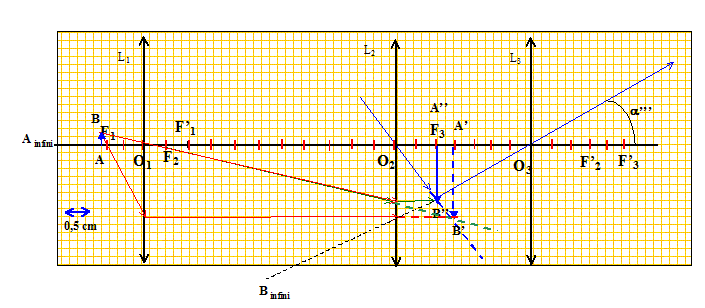Schéma de conjugaison :   Faire le schéma en plaçant les lentilles, AB, A'B', A"B".  Préciser la nature des images A'B', A"B" et de l'image définitive. L'image définitive est virtuelle ; A'B' et A"B" sont réelles, situées respectivement à droite de L1, de L2. Ce type d'oculaire peut-il servir de loupe ? oui. Loupe : lentille convergente ; l'objet réel doit être placé entre le centre optique de la lentille et le foyer principal objet ; l'image est virtuelle. On grave et on colore une graduation sur une plaque de verre. Où faut-il la placer ? Sur l'objet AB. Utilisation des formules de conjugaison : L1 ( 8 d) O1F'1 = 12,5 cm ;  L2 ( 2 d) O2F'2 = 50 cm ;  L3 ( 4 d) O3F'3 = 25 cm. On écrite en bleu et en gras les distances algébriques.   O1O2 = 58 cm ; O2O3 = 37,5 cm. Déterminer les valeurs numériques de O2A", O2A', O1A', O1A. L'image définitive étant à l'infini, l'objet A"B" est en F3. O2A" = O2O3 +O3F3 =O2O3 -F3 O3 =37,5-25 = 12,5 cm. Formule de conjugaison pour L2 : 2 = 1/O2A' - 1/O2A'' ; 1/O2A'' =1/O2A' -2 = 1/0,125-2 = 8-2 = 6 ; O2A' = 1/6 =16,7 cm ( 16,667) O1A' = O1O2+O2A' =58+16,7 = 74,7 cm. Formule de conjugaison pour L1 : 8 = 1/O1A' - 1/O1A ; 1/O1A =1/O1A' -8 = 1/0,747-8 = 1,34-8 = -6,66 ; O1A = 1/(-6,66) = -15 cm. Déterminer les valeurs numériques des grandissements des lentilles L1 et L2. g1 = A'B' / AB ; g2 = A"B" / A'B'. g1 = A'B' / AB = O1A' / O1A = -15/ 74,7 = -4,98 = -5,0. g2 = A"B" / A'B' = O2A"/ O2A' = 12,5 /16,7 = 0,75. Grossissement du montage : La puissance de l'oculaire en dioptries est définie comme étant Poc = a"'/A'B' avec a "' langle sous lequel l'oeil voit la lumière sortante par rapport à l'axe optique. Déterminer la puissance de l'oculaire. tan a"' = A"B"/ f'3 = A"B" / A'B' * A'B'/ f'3 = g2 * A'B'/ f'3 . Si l'angle est petit on peut confondre la tangente et la mesure de l'angle en radian. a"' voisin g2 * A'B'/ f'3 ; Poc voisin g2 / f'3 = 0,75/0,25 = 3. Déterminer la puissance de ce "microscope" Pmic = a "' / AB. a"' voisin g2 * A'B'/ f'3 = g2 * A'B'/AB*AB/ f'3 =g2 *|g1|AB/ f'3. Pmic =g2 *|g1|/ f'3 = Poc*|g1| =3*5 = 15. Il est d'usage de définir pour le grand public le grossissement commercial G = | a "' / a| où a est l'angle sous lequel l'oeil nu verrait l'objet AB à une distance d=25 cm devant lui. Calculer G. a"' voisin g2 * A'B'/ f'3 ; tan a = AB/d = AB/0,25 = 4 AB Si l'angle est petit on peut confondre la tangente et la mesure de l'angle en radian. a voisin 4 AB. G voisin g2 * A'B'/ ( 4 AB) f'3 = g2 *|g1|/ (4f'3 ) = Pmic /4 =15/4 = 3,8.

retour -menu