Les cyclotrons : équation différentielle et nombres complexes concours ITPE 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Les vecteurs sont écrits en gras et en bleu. On étudie un proton considéré comme une masse ponctuelle m = 1,6 10-27 kg, de charge e = 1,6 10-19 C et de vitesse instantanée v. Il n'est pas relativiste : 10 v < 3 108 m/s. On négligera toute force dissipative dans ce problème. Il est dans une zone de l'espace où règne un champ électrique E et un champ magnétique B. On rappelle que la force de Lorentz est : F = e(E + v^ B) Bilan des forces : Quelle est l'unité du champ électrique ? V m-1. Rappeler l'ordre de grandeur du champ magnétique à la surface de la terre. composante horizontale du champ magnétique terrestre : 2 10-5 T. Dans le cas du proton ci-dessus évoluant à v = 0,01 c dans un champ magnétique plus intense que celui de la terre, Justifier que le poids est toujours négligeable. mg = 1,6 10-27 * 9,8 = 1,6 10-26 N force magnétique : e v B ; on choisit v = 3 106 m/s et B = 0,01 T. evB = 1,6 10-19* 3 106 *0,01 = 5 10-15 N, valeur très supérieure à celle du poids. Variation de l'énergie cinétique :   Rappeler la définition d'une énergie potentielle. Energie potentielle : énergie qui est échangée par un corps qui se déplace sous l'action d'une force conservative. L' énergie potentielle, définie à une constante près, ne dépend que de la position du corps dans l'espace. " potentielle" signifie que cette énergie peut être emmagasinée par un corps et peut ensuite être transformée en une autre forme d'énergie. Quel est le lien entre E et le potentiel V ? E = - grad V. Démontrer que l'énergie potentielle dont dérive la force de Lorentz est Ep = eV + Cte. F = eE + ev^ B. Une force perpendiculaire à la vitesse ne travaille pas : le travail de la force de Lorentz se résume donc au travail de eE. travail élémentaire au cours du déplacement dl : dW = eE . dl = -e grad V. dl. travail au cours d'un déplacement fini d'un point 1 à un point 2 : W = -e( V2-V1) La variation de l'énergie potentielle au cours de ce déplacement est l'opposé du travail de la force : DEp = Ep2-Ep1 = e( V2-V1) Par suite l'énergie potentielle vaut : Ep = e V + Cte. Déterminer la variation d'énergie cinétique du proton allant de A vers C. L'énergie mécanique étant constante, la variation d'énergie cinétique est l'opposé de la variation de l'énergie potentielle. DEc = e( V1-V2).    Trajectoire dans un champ magnétique seul. On travaille dans un référentiel galiléen ( O, ux, uy, uz) orthonormé direct. B = Buz ; E=0 dans cette partie. A t=0, le proton est en O avec une vitesse initiale v(0) = v0 ux.  Quelle est la définition d'un référentiel galiléen ? dans ce référentiel le principe d'inertie ou 1ère loi de Newton s'applique " un point matériel pseudo-isolé demeure dans son état de repos ou de mouvement rectiligne uniforme". Démontrer que le mouvement est plan. conditions initiales : vitesse initiale v(0) = v0 ux, portée par l'axe Ox.  La force magnétique initiale est portée par l'axe Oy. F = ev^ B ; B = Buz ; v(0) = v0 ux ; F = e v0 ux^Buz = e v0B(-uy) Le mouvement est dans le plan (Ox, Oy), perpendiculaire à B. Déterminer les deux équations différentielles du mouvement liant x(t) et y(t). On posera we =eB/m. La seconde loi de Newton s'écrit : ev^ B= ma. v vx=dx/dt vy=dy/dt vz=0 B 0 0 B v^ B B dy/dt -B dx/dt 0 ev^ B eB dy/dt -eB dx/dt 0 ev^ B= ma. eB dy/dt = m d2x/dt2. wedy/dt =d2x/dt2. -eB dx/dt = m d2y/dt2. -wedx/dt =d2y/dt2. d2z/dt2=0. Soit p(t) = x(t) + jy(t) avec j2=-1. Ecrire l'équation différentielle de p(t). dp(t)/dt = dx(t)/dt + jdy(t) /dt d2p(t)/dt2 = d2x(t)/dt2 + jd2y(t) /dt2 dp(t)/dt = 1/ we (-d2y/dt2 +jd2x/dt2)= 1/ we (j2d2y/dt2 +jd2x/dt2) dp(t)/dt = j/ we (jd2y/dt2 +d2x/dt2) ; dp(t)/dt =j/ wed2p(t)/dt2.    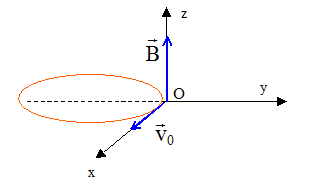Trajectoire. Quelles sont les deux conditions initiales sur p(t) ? A t=0, le proton est en O avec une vitesse initiale v(0) = v0 ux.  p(0) = 0 ;  dp(0)/dt = dx(0)/dt + jdy(0) /dt= v0 ;  dp(0)/dt =v0 . Résoudre l'équation différentielle et déterminer p(t).  dp(t)/dt =j/ wed2p(t)/dt2 s'écrit :  d2p(t)/dt2 +jwedp(t)/dt =0 équation caractéristique : r2 + jwer=0 ; solutions r1=0 et r2= - jwe. p(t) = A + B exp(- jwet) à t = 0 : 0 = A+B soit B = -A dp(t)/dt = - jweB exp(- jwet) ; dp(0)/dt = v0=- jweB ; B = jv0/we p(t) = jv0/we ( exp(- jwet)-1). En déduire x(t) et y(t). exp(- jwet) = cos(wet) -j sin(wet) ; p(t) = jv0/we[cos(wet)-1 -j sin(wet)] p(t) =v0/wesin(wet) + jv0/we[cos(wet)-1] = x(t) + jy(t) x(t) = v0/wesin(wet) ; y(t) = v0/we[cos(wet)-1]. La trajectoire est un cercle. Démontrer que le rayon est R =mv0/(eB).  y+v0/we =v0/wecos(wet) x2+(y+v0/we)2 = [v0/we]2 [sin2(wet) +cos(wet)2 ] = [v0/we]2 centre du cercle A (0 ; -v0/we) ; rayon R = v0/we = mv0/(eB). Montrer que le temps Dt mis pour décrire un demi cercle est indépendant de v0. demi circonférence : pR=pmv0/(eB). La valeur de la vitesse est constante égale à v0 : la force magnétique, perpendiculaire à la vitesse, ne modifie pas la valeur de la vitesse. durée Dt = pR/v0 = pm/(eB).  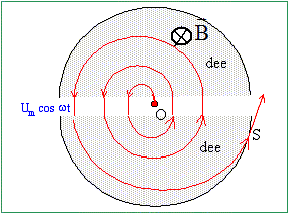Dessiner le cercle ainsi que le repère (O, x, y).    Le premier cyclotron 1,2 MeV construit se compose d'un électro-aimant dans l'entrefer duquel on loge une boîte métallique de diamètre 28 cm ( 11 pouces) maintenue sous vide. La chambre contient deux électrodes creuses en forme de "D" entre lesquelles est appliquées une tension alternative de 4000 V à haute fréquence. En son centre se trouve une source qui fournit des protons. Les protons décrivent une trajectoire dans le plan médian, du centre jusqu'au bord. Entre les dees, la seule force prépondérante est celle due à E. 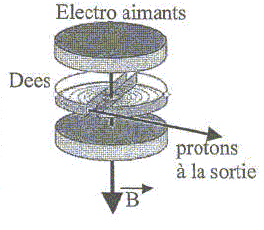Dans les dees, la seule force prépondérante est celle due à B.  Dessiner le cyclotron "vu d'en haut" en représentant soigneusement la trajectoire des protons ainsi que le champ magnétique B. B est perpendiculaire à la figure, dirigé vers l'arrière.  Calculer la vitesse de sortie des protons d'énergie cinétique finale 1,2 MeV.  1,2 MeV = 1,2 * 1,6 10-13 J =1,92 10-13 J ;  ½mv2= 1,92 10-13. v = [2*1,92 10-13/1,67 10-27]½ =1,516 107 = 1,5 107 m/s. Quelle énergie cinétique ( en keV) prennent-ils à chaque tour ( deux passages entre les dees à chaque tour) ?  A chaque passage entre les dees, l'énergie cinétique augmente de : eU 2 eU = 2*1,6 10-19*4000 =1,28 10-15 J = 8 000 eV = 8 keV. Combien de tours font-ils dans le cyclotron ? 1,2 MeV = 1200 keV ; 1200/8 =  150 tours. Quelle est la fréquence de la tension alternative ? A.N avec Rmax = 14 cm.  Pour une accélération maximale, à chaque demi tour, la tension alternative doit changer de signe et prendre sa valeur maximale. La demi période de la tension alternative est égale à la durée d'un demi tour. ½T=pR/v ; f = 1/T = v/(2pR) =1,516 107 /(6,28*0,14) = 1,72 107 Hz. Quelle est la valeur du champ magnétique B ?  R= mv/(eB) soit B = mv/(eR) = 1,67 10-27 *1,516 107 /(1,6 10-19 *0,14) =1,13 T. Pourquoi la technologie du type cyclotron avec ses dees a été abandonnée dans les années 50 au profit d'anneaux d'accélération ?  La quantité de fer pour construire l'aimant qui engendre le champ magnétique dans tout le volume de l'accélérateur devient trop importante. Pertes de Larmor du cyclotron. Le proton accéléré rayonne. La puissance perdue est P = e2 / (6p e0 c3) a2 avec a : accélération, e0 = 8,8 10-12 F m-1, c = 3 108 m/s. Estimer la puissance du rayonnement lors du dernier tour.  accélération centripère a = v2/R=(1,516 107)2 / 0,14 = 1,64 1015 m/s2. P = (1,6 10-19)2/ [6*3,14* 8,8 10-12 *(3 108)3] =9,38 10-39 W. Estimer l'énergie perdue en eV lors du dernier tour. P *2Dt avec Dt = ½T = 0,5/f = 0,5/1,72 107 =2,9 10-8 s P= 9,38 10-39*2*2,9 10-8 = 5,45 10-46 J 5,45 10-46 /1,6 10-19 = 3,4 10-27 eV. L'évolution des accélérateurs de protons. En supposant que le champ magnétique est sensiblement le même dans les différents cyclotrons à protons, estimer l'énergie de sortie du 60 pouces construit en 1939.  On passe d'un diamètre de 11à 60 pouces : 60/11 = 5,5. vitesse de sortie : v = eBR/m : si le rayon est multiplié par 5,5, alors v2 est multipliée par 5,52 =30. L'énergie de sortie est sous forme cinétique : 1,2 MeV correspond à 11 pouces d'où : 30*1,2 = 36 MeV. Pour des énergies de 15 MeV, l'expression correcte de la pulsation du cyclotron devient eB/m [1-v2/c2]½. En quoi cette expression est génante pour le fonctionnement du cyclotron ?  La fréquence du champ électrique dépend de la vitesse. Comment le synchrocyclotron de Mc Millan (1945) résolut-il ce problème ? Un synchrocyclotron est un cyclotron dont la fréquence du champ électrique est lentement diminuée afin de compenser l'augmentation de masse des particules accélérées quand leur vitesse s'approche de celle de la lumière. Quest-ce qu'un synchrotron ? Le synchrotron est un dispositif permettant l'accélération de particules chargées.L'énergie atteinte par les particules est très élevée. Comme dans le cyclotron, les particules décrivent des cercles entre les pôles d'électro-aimants disposés en anneau. A chaque tour les particules sont accélérées. Les particules sont confinées sur le cercle, en ajustant le champ magnétique à l'énergie atteinte. On injecte les particules "en bouffées" dans l'anneau, à champ magnétique faible. Ces dernières sont accélérées, puis éjectées quand le champ magnétique atteint sa valeur maximale.

retour -menu