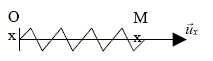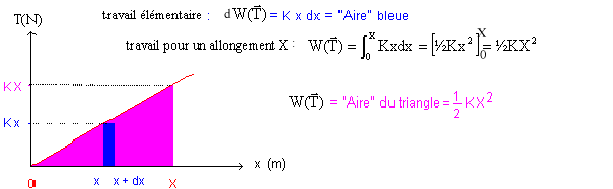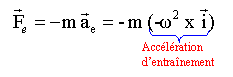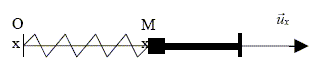Etude de systèmes oscillants, amortissement, oscillations forcées. concours interne ITPE 07

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

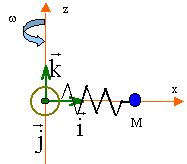
Etude de systèmes oscillants.

L’objet de l’étude est un point matériel M de masse m accroché à un ressort de longueur à vide l₀ et de raideur k. Le ressort est fixé en O et est enfilé sur une tige horizontale définissant l’axe u_x. Le point M est lui aussi enfilé sur la tige.

Les frottements sont négligés dans les questions 1 et 2 et n’interviennent que dans les questions 3 et 4. On les modélise alors par une force décrite à la question 3. On pose : OM = x.

Valeurs numériques : m = 100 g ; k= 1 N.m^-1 ; l₀= 5 cm ; g = 9,8 m. s^-2.

Introduction.

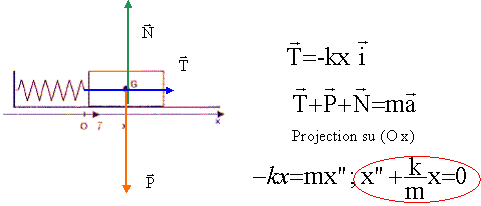
Faire un bilan des forces et établir l’équation différentielle qui régit le mouvement de M.

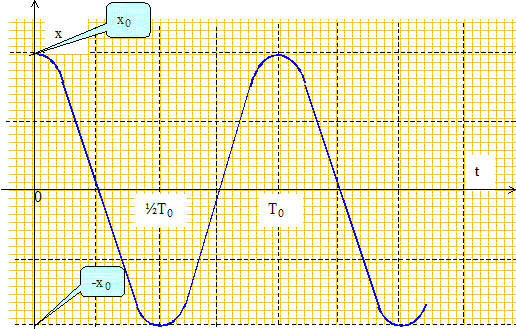
Montrer que le mouvement est harmonique et exprimer sa pulsation propre w₀ en fonction des données du problème. Calculer w₀.

L'équation différentielle ci-dessus est celle d'un oscillateur harmonique de pulsation w₀ telle que :

w₀ = [k/m]^½ = [1/0,1]^½ = 3,16 rad s^-1.

Résoudre l’équation différentielle sachant qu’à t=0 :

le ressort est tendu, OM(t=0) = x₀ (> l₀), et que le point M est lâché sans vitesse initiale.

Solution du type x= A cos (w₀t+F).

à t = 0 x= x₀ = A cos F d'où A= x₀ et F =0 ; x(t) = x₀ cos (w₀t).

Tracer l’allure de x(t).

Montrer que la force exercée par le ressort est conservative.

Le travail d'une force conservative ne dépend que des positions initiale et finale, peu importe le chemin suivi.

Effectuer un bilan énergétique et retrouver l’équation différentielle du mouvement.

L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle. En l'absence de frottement celle-ci reste constante.

½mv²+½kx²=Cte

Dériver par rapport au temps : m v v' + k x x' =0

Or v= x' et v' = x" d'où en divisant chaque membre par x' : m x" + kx=0.

Tige en rotation. La tige est animée d’un mouvement de rotation uniforme de vitesse angulaire w constante par rapport au référentiel du laboratoire supposé galiléen. Etablir l’équation différentielle du mouvement du point M. Discuter la forme des solutions. On choisit un référentiel R lié à la tige :

Dans le référentiel R lié à la tige, la vitesse du point matériel s'exprime suivant : ; l'énergie cinétique de M s'écrit : E_c = ½ m x'².

La tige est horizontale, alors l'énergie potentielle de pesanteur ne varie pas et on peut la choisir arbitrairement nulle ( en prenant l'origine des altitudes en O, origine du repère).

le référentiel R n'est pas galiléen, il faut tenir compte des forces d'inertie :

La puissance de la force de Coriolis est nulle ( la force de Coriolis est perpendiculaire au vecteur vitesse).

force d'inertie d'entraînement :

La puissance de cette force, colinéaire au vecteur vitesse n'est pas nulle : cette force dérive d'une énergie potentielle.

travail de la force d'entraînement :

l'énergie potentielle est l'opposé du travail :

dE_p = -mw²x dx ; E_p = -½mw²x² + Cte

On choisit l'origine de cette énergie potentielle à l'abscisse x=0, dans ce cas la constante d'intégration est nulle.

l'origine de cette énergie potentielle est prise à l'abscisse x = l₀. Dans ce cas la constante est nulle.

L'énergie mécanique s'écrit alors : ½ m x'² -½mw²x² + ½ k(x-l₀)² ; celle ci est constante en l'absence de frottement.

La dérivée de l'énergie mécanique par rapport au temps est nulle

Pour obtenir l'équation différentielle du mouvement de M, dériver l'expression de l'énergie par rapport au temps.

d'où : ½ m 2 x" x' - ½ mw² 2 x x' + ½ k . 2 (x-l₀) x' = 0

diviser par m x' , supposée non nulle, chaque terme : x" - w² x + k /m (x-l₀) =0.

On pose w₀² = k / m

x" - w² x + w₀² x = kl₀/m

x" + (w₀² - w²) x = w² l₀ (1)

solution particulière de l'équation avec second membre :

x_e = w² l₀ / (w₀² - w²).

On observe des oscillations autour de cette position d'équilibre si w₀² > w²

Dans ce cas, solution générale de l'équation sans second membre :

La solution générale de l'équation différentielle (1) est : x_e + x₁.

A₁ et A₂ sont des constantes déterminées à partir des conditions initiales.

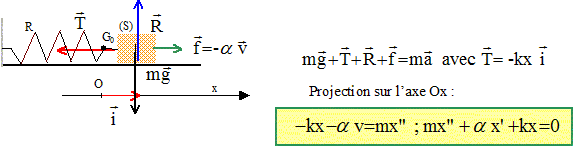
Les vecteurs sont écrits en gras et en bleu.

La tige est à nouveau fixe dans le référentiel de l’expérimentateur. On tient compte des frottements qui s’appliquent en M en les modélisant par une force

f = -a v. (a > 0) où v est la vitesse du point M.

Quelle est la dimension de a ?

[a ]= force . vitesse^-1 et [force] = masse. accélération = masse . longueur . temps^-2 et [vitesse] = longeur. temps^-1.

[a ] = masse . longueur . temps^-2 . longueur^-1.temps ; [a ] = masse . temps^-1 ; [a ] = M T^-1.

Etablir la nouvelle équation différentielle du mouvement.

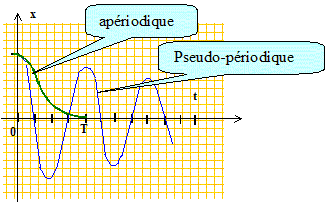
A quelle condition le point M peut-il osciller ?

On calculera a_lim, valeur limite de a pour observer des oscillations, en fonction de w₀.

L'équation différentielle s'écrit : x" + a/m x' + w₀²x=0. (1)

L'équation caractéristique s'écrit : r² + a/m r + w₀²=0 ; discriminant : D= [a/m]²-4w₀².

Si le discriminant est négatif on observe des oscillations amorties.

cas limite : [a_lim/m]²= 4w₀² ; a_lim=2mw₀.

Donner la forme des solutions et tracer l’allure de x(t) dans les deux cas : a_lim< a et a_lim > a.

si D <0 : pulsation w² = w₀² - [a/(2m)]²
solution : x = B exp( -a/(2m)t) sin (wt+j), régime pseudopériodique ( amortissement faible)

L’énergie mécanique est-elle conservée ? Expliquer.

La force de frottement n'est pas une force conservative : l'énergie mécanique n'est pas conservée.

En déduire que, pour t tendant vers l'infini , x tend vers une valeur x_lim , que l’on définira.

 x = B exp( -a/(2m)t) sin (wt+j) : le terme en exponentielle tend vers zéro : x=0.

Les vecteurs sont écrits en gras et en bleu.

L’extrémité du ressort M, où est accrochée la masse m, est solidaire d’un petit moteur qui applique au point M une force supplémentaire F, telle que :

F = F₀ cos( w_et )u_x.

Le moteur effectue des oscillations et entraîne le point matériel M grâce à la force F. La pulsation w_e de la force, et du moteur, est ajustable par l’expérimentateur. Le déplacement sur la tige s’effectue toujours avec la force de frottement : f = -a v.

Ecrire l’équation différentielle vérifiée par x(t).

L'équation différentielle s'écrit : x" + a/m x' + w₀²x= kF₀/m cos( w_et ). (2)

Préciser le mouvement de M en régime permanent et montrer que x(t) est de la forme :

La solution de l'équation sans second membre est amortie exponentiellement : elle correspond à un régime transitoire.

La solution particulière correspond au régime permanent.

On se place au bout d'un temps suffisamment long pour que le régime permanent soit atteint : la solution de l'équation sans second membre est alors négligeable devant la solution particulière. L'excitateur force l'oscillateur à osciller à la fréquence de l'excitateur.

x(t) =X₀ cos( w_et ) ou encore en notation complexe : X =X₀ exp (jw_e t).

Donner l’expression de X₀.

dérivées : X' = X₀ jw_e exp(jw_e t) ; X" = X ₀ (-w_e²) exp(jw_e t) ;

repport dans (2) :

X ₀ (-w_e²) exp(jw_e t) +a/m X ₀ jw_e exp(jw_e t) + w₀² X ₀ exp(jw_e t) =kF₀/m exp(jw_e t)

simplifcation par exp(jw_e t) :

X₀ (w₀² -w_e² +a/m jw_e ) = F₀/m

X₀ = F₀/m / [(w₀² -w_e² +a/m jw_e )]

module de ce nombre complexe : X₀=kF₀/m . [(w₀² -w_e² )²+(a w_e /m )²]^-½.

On fait varier w_e.

Que se passe-t-il quand w_e est proche de w₀ ? Comment appelle-t-on ce phénomène ?

X₀ tend vers un maximum X_maxi =kF₀/(a w₀) : phénomène de résonance d'amplitude.

Que se passe-t-il quand w_e est très différent de w₀ ?

X₀ tend vers zéro ( si w_e devient grand ) ou vers une valeur minimale ( si w_e devient très faible ).

Que représente le « facteur de qualité » Q du système ? Comment le définir ici en fonction de a et w₀ ?

Un facteur de qualité élevé indique une résonance aigue ( X_maxi très grand) ; par contre un facteur de qualité faible, indique une résonance floue.

Q = w₀ m/a

A quelle condition sur Q peut-on observer un maximum pour l’amplitude ? Pour la vitesse ?