Electrocinétique : fonction de transfert, diagramme de Bode Concours ITPE 2002. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

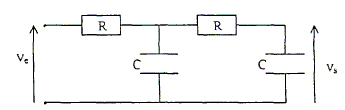
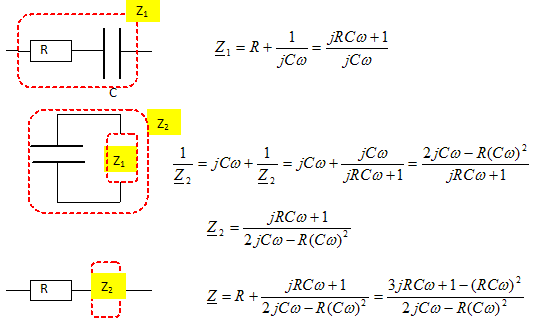
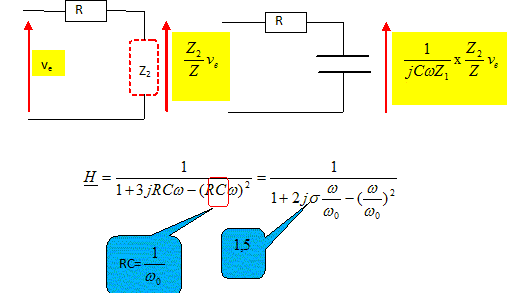
On étudie en régime sinusoïdal, le circuit ci-dessous constitué de deux résistor identiques R= 10 kiloohms et de deux condensateurs de même capacité C= 10 nF. La tension d'entrée est fournie par un générateur basse fréquence et s'écrit ve(t)=Em cos(wt) ; la tension de sortie est notée vs(t)=Vm cos(wt+F). L'étude du filtre sera effctuée en utilisant la notation complexe ve=Em e(jwt) et vs=Em e(jwt+F) avec j2=-1. Déterminer, de manière qualitative et sans calculs, en utilisant la notion d'impédance, la nature du filtre étudié. A très basse fréquence le condensateur se comporte comme un interrupteur ouvert ( impédance infinie). Vs diffère de zéro. A haute fréquence, le condensateur se comporte comme un interrupteur fermé ( impédance nulle). Vs est nulle. Donc filtre passe bas. Déterminer la fonction de transfert H(jw) = vs/ ve.   On mettra H sous la forme : H= 1 1+2j s w/w0 -[w/w0]2 w0 = 1 RC = 1 104*10*10-9 = 104 rad/s. On pose H= G exp(jF) et x = w/w0. Exprimer le gain G(x) puis le gain en décibels noté GdB = 20 log G. H(x) = 1 1+3jx-x2 = (1-x2)-3jx (1-x2)2+ 9x2   G (x) = 1 [(1-x2)2+ 9x2]½ ; GdB = -10 log [(1-x2)2+ 9x2] Déterminer le comportement asymptotique de GdB, c'est à dire l'expression simplifiée de GdB pour x<<1 ( basse fréquence) et pour x>>1 ( haute fréquence). x<<1 : GdB ~ -10 log 1 ~ 0. x>>1 : GdB ~ -10 log x4 ~ -40 log x. 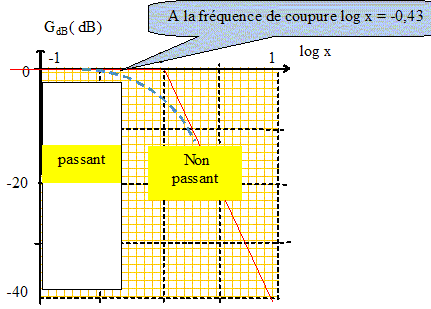Tracer le diagramme de Bode asymptotique en portant GdB en ordonnée et log x en abscisse.   Quelle est la nature du filtre ? Passe bas. GdB=0 ; F~ 0 : passant ; GdB= -40 log x ; F~ 90 : filtré. Calculer la fréquence de coupure fc à -3 dB. -3 = -10 log [(1-x2)2+ 9x2] ; 100,3 = 2 = (1-x2)2+ 9x2 Changement de variable X= x2 d'où en effectuant : X2+7X-1=0 Résoudre ( retenir la valeur positive ) : X = 0,14 et x = 0,374 ( log x = -0,43) Par suite la pulsation de coupure wc vaut : 0,374 w0 = 3,74 103 rad /s. fc= wc /(2p) = 3,74 103 / 6,28 = 596 Hz. Calculer le gain en décibels puis la valeur de G pour une tension d'entrée de fréquence 5 kHz. 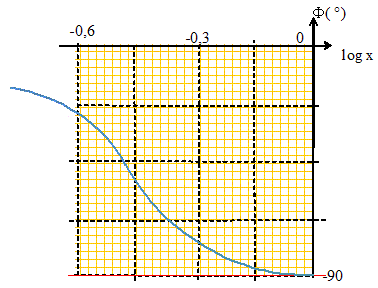w = 2p f = 6,28*5000 = 31400 rad/s ; x = w /w0 =3,14 ; G (x) = 1 [(1-3,142)2+ 9*3,142]½ = 7,7 10-2 GdB = -10 log [(1-3,142)2+ 9*3,142] = -22 dB Donner l'expression de tan F où F est le déphasage entre la tension de sortie et la tension d'entrée ainsi que son intervalle de variation lorsque x varie. tan F = -3x 1-x2 x 0 0,25 0,374 0,5 1- log x xxxxxx -0,60 -0,43 -0,3 0 tan F 0 -0,8 -1,3 -2 tend vers moins l'infini F (°) 0 -38 -52 -63 -90 Tracer l'allure du graphe de F en fonction de log x.

retour -menu