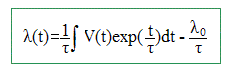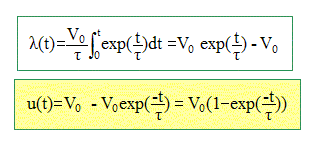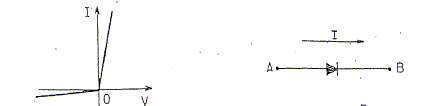régimes transitoires dans un circuit RC concours ITPE 2002 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

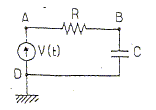
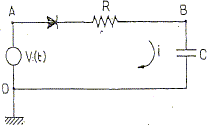
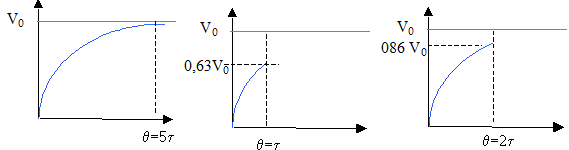
On considère le circuit ci-dessous comprenant un condensateur de capacité C, une résistance R et un générateur de tension. On pose VA-VD= V(t) , VB-VD = u(t). La tension aux bornes du générateur est v(t), fonction du temps à priori quelconque. Etablir l'équation différentielle reliant u(t) à v(t). Additivité des tensions : V(t) = R i + u(t) avec i= dq/dt et q= C u(t) soit i = Cdu(t)/dt). V(t) = RCdu(t)/dt + u(t). On pose t = RC d'où : du(t)/dt + 1/t u(t) = V(t) / t (1) On cherche la solution de cette équation sous la forme : u(t) = l(t) exp(-t/t). Etablir l'équation différentielle vérifiée par l(t) ? du(t) / dt = dl(t)/dt exp(-t/t) - l(t)/ t exp(-t/t) Repport dans (1) : dl(t)/dt exp(-t/t) - l(t)/t exp(-t/t) + l(t) /texp(-t/t) = V(t) /t. dl(t)/dt exp(-t/t) =V(t) /t. Comment choisir t pour que l (t) n'y intervienne plus que par sa dérivée dl/dt ? On pose t = RC. A.N : R= 1 MW ; C= 1 nF. Calculer t. 1 MW = 106 W C= 1 nF = 10-9 F ; RC = 10-3 s. Sachant qu'à t=0 on avait u(t) = u0, exprimer l(t) à l'aide d'une intégrale définie.  dl(t)/dt =V(t) /t exp(t/t) u(t) = l(t) exp(-t/t) ; u(0) = l0. On s'intéresse à une tension d'excitation V(t) en crénau. A l'instant t=0 la charge du condensateur est nulle. Calculer u(t). Donner l'allure de u(t) suivant la valeur du rapport q/t en particulier dans les cas limites q/t<<1 et q/t >>1.   q/t<<1 : u(t) = 0, le condensateur n'a pas le temps de se charger. q/t >>1 : le condensateur a le temps de se charger, après un régime transitoire, u(t) = V0.    Introduction d'une diode. On assimile la caractéristique d'une diode à deux demi-droites qui, dans le plan (V, I) ont pour équations : I= V/Ri pour V<=0 et I= V/Rd pour V>0 où V est la différence de potentiel VA-VB et où I est compté positivement de A vers B. 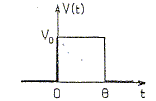Sauf avis contraire, on passera, après calculs avec Ri et Rd finies, aux limites Ri infinie et Rd nulle : le courant est très faible lorsque la diode est polarisée en inverse ( V<0) ; lorsque la diode est polarisée en direct ( V>0) elle se comporte comme une résistance négligeable par rapport aux autres résistances du circuit. On considère le montage suivant et on s'intéresse au cas de l'excitation en crénau. On note u(t) = VB-VD. A l'instant t=0, u(0) = 0. Etude de la charge : Entre t=0 et t= q, comment la diode est-elle polarisée ? Quelle est la valeur de u(q) ? A.N : R= 10 kW ; C= 1 mF ; q= 1 s ; V0= 30 V La diode est passante. RC = 104*10-6 = 10-2 s. La constante de temps étant très inférieure à q, le condensateur a le temps de se charger complétement : u(q ) =V0 = 30 V.  Etude de la décharge : Calculer u(t) à Ri finie. Que se passe t-il si Ri est infinie ? Le courant de décharge est de sens contraire au courant de charge ( discontinuité de l'intensité). à t > q : V(t) = 0 ;additivité des tensions : u(t) - (Ri +R) i = 0 avec i = - dq/dt = -Cdu(t)/dt d'où : u(t) + (Ri +R)C du(t)/dt = 0 On pose t'=(Ri +R)C ; u(t) = V0 exp(-t/t'). Si Ri est infinie, la diode est non passante : le condensateur ne se décharge pas et u(t) = V0.   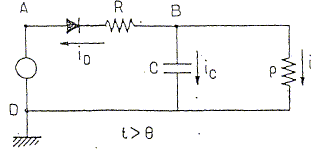Pour t >0 on branche en parallèle sur le condensateur une résistance de valeur r. On veut calculer la dépendance temporelle du courant i(t) circulant dans cette résistance. Etablir l'équation différentielle vérifiée par u(t). admittance complexe de l'ensemble R, r : Y1 = jCw + 1/r =( jCrw + 1)/r impédance complexe correspondante : Z1 = r / ( jCrw + 1). impédance complexe de l'ensemble : Z =R+Rd+ r / ( jCrw + 1). Z = [(R+Rd) ( jCrw + 1) +r ]/ ( jCrw + 1). Les grandeurs soulignées sont des nombres complexes V(t) = Z id ; u(t) = Z1id d'où : V(t) Z1 = u(t)Z. V(t) r = u(t) [(R+Rd) ( jCrw + 1) +r ]. V(t) r = u(t) [(R+Rd+r) + Crjw (R+Rd) ]. Or multiplier par jw correspond àla dérivation d/dt. d'où : V(t) r = (R+Rd+r) u(t) + Cr(R+Rd)du(t)/dt On pose : t' = Cr(R+Rd) / (R+Rd+r) du(t)/dt + 1/t' u(t) = V(t) / [C(R+Rd) ]. (2) Calculer u(t). solution particulière de (2) en régime permanent : u(t) = V(t) r / (R+Rd+r) solution générale de : du(t)/dt + 1/t' u(t) =0 : u(t) = A exp(-t/t') solution générale de (2) : u(t) = A exp(-t/t') + V(t) r / (R+Rd+r) A l'instant initial, u(0) = 0 d'où A = -V(t) r / (R+Rd+r) u(t) = V(t) r / (R+Rd+r) [1-exp(-t/t')] Dans le cas du signal créneau et de Rd =0 : u(t) = V0 r / (R+r) [1-exp(-t/t')]. Quelle est la nouvelle valeur de la constante de temps t' intervenant dans le circuit ? t' = Cr(R+Rd) / (R+Rd+r)  En déduire la dépendance temporelle des courants i et iD.  i(t) = u(t) / r ;( Rd+R)id (t) + u(t) = V0. id (t) = (V0-u(t) ) / ( Rd+R)

retour -menu