Moteur à courant continu à aimants permanents ; hacheur série à transistor bipolaire concours technicien laboratoire 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

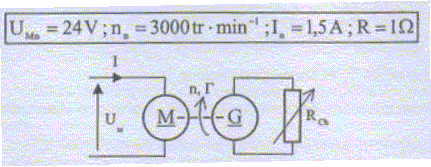
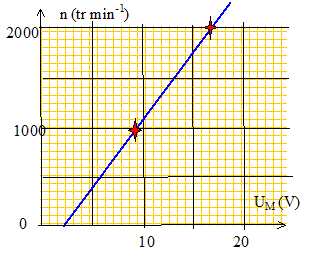
Le moteur est alimenté par un générateur de tension 24 V. Pour le point de fonctionnement nominal, calculer la force contre électromotrice (f.c.e.m) En. UM = En+RIn ; En = UM-RIn = 24-1*1,5 = 22,5 V. Sachant que la f.c.e.m est proportionnelle à la fréquence de rotation n, montrer que son coefficient de proportionnalité k vérifie : E= k n avec k = 0,45 V s tr-1. Pour le fonctionement nominal : k = En/ n avec n = 3000/60 = 50 tr /s. k = 22,5/50 = 0,45 V s tr-1.  Déterminer les valeurs en tr s-1 et en tr min-1 de la fréquence de rotation n pour les deux valeus suivantes de UM, 9 V et 16,5 V, l'intensité du courant d'induit gardant sa valeur nominale : I = In =1,5 A. UM = En+RIn = kn +RIn =0,45 n + 1,5. n = (UM-1,5) / 0,45 ; n1 = (9-1,5)/0,45 = 16,7 tr s-1 = 1000 tr min-1. n2 = (16,5-1,5)/0,45 = 33,3 tr s-1 = 2000 tr min-1. Tracer la caractéristique donnant le fréquence de rotation n en fonction de la tension UM à courant d'induit constant. n = (UM-1,5) / 0,45 = 2,22 UM-3,33 tr s-1 ; n = 133,33 UM-200 tr min-1.   Quelle est la puissance électrique, fournie par le générateur de tension 24 V, notée Pgéné lorsque le moteur est à son régime nominal ? Pgéné = 24*1,5 = 36 W. Quelle est la puissance électromagnétique, notée Pélec mise en jeu dans le moteur pour être convertie ensuite en puissance mécanique sur l'arbre ? Pélec = En In =22,5*1,5 = 33,75 W~ 33,8 W. On suppose que les pertes mécaniques et les pertes magnétiques sont négligeables. Que vaut la puissance mécanique notée Pméca du moteur en régime nominal ? Pméca = Pélec ~33,8 W. Déterminer la valeur du rendement hM du moteur. hM =Pméca /Pgéné =33,75/36 ~ 94 %. Sachant que la puissance mécanique disponible sur l'arbre du moteur peut se mettre sous la forme Pméca = G W où G est le moment du couple moteur exprimé dans le système S.I et W la vitesse angulaire de rotation exprimée en rad/s, déterminer ou rappeler : la relation entre W et n ( tr/s). W = 2p n. l'unité de G : mN. la valeur de G en régime nominal. G = Pméca / W =33,75 / (2*3,14*50)=0,107 ~0,11 mN. En déduire l'expression donnant G en fonction de k et I ; calculer la valeur du coefficient liant G et I. Pméca = En In = k n In = G W = G 2pn. On identifie : kIn = G 2p ; G =kIn /(2p) =0,45/6,28 In ; G =7,2 10-2 In. Quelle sera l'influence d'une augmentation de la résistance de charge Rch de la machine fonctionnant en génératrice sur la fréquence de rotation n du groupe tournant ? La génératrice crée un courant induit qui par ces effets électromagnétiques s'oppose à la cause qui lui donne naissance : ce courant a donc le sens contraire au courant du fonctionnement en moteur et il en résulte un couple résistant proportionnel à l'intensité. La charge impose la valeur de l'intensité ; la tension d'alimentation impose la vitesse de rotation.   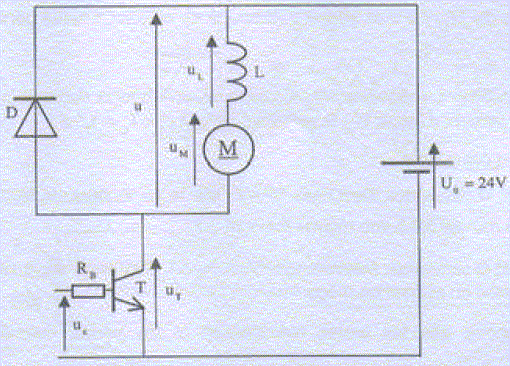Hacheur série à transistor bipolaire. On adopte les notations suivantes : u(t), uL(t), uM(t) et uT(t) désigne respectivement les valeurs instantanées des tensions u, uL, uM et ur. <u>, <uL> et <uM> désignent respectivement les valeurs moyennes des tensions u, uL et uM. La période du hacheur est notée T0 et son rapport cyclique a. Le transistor T fonctionne en commutation et se comporte comme un interrupteur commandé, supposé parfait. Dans l'intervalle [0; aT0], uc= 5 V, ur=0 V ( interrupteur fermé). Dans l'intervalle [ aT0 ; T0 ], uc= 0 V, iT=0 A ( interrupteur ouvert) ; iT étant l'intensité du courant collecteur du transistor T. La diode est supposée parfaite, elle ne possède que deux états : si u >0 V, iD= 0 A ( diode bloquée) ; si u =0 V, iD> 0 A ( diode passante) ; iDétant l'intensité du courant dans la diode. La bobine est supposée parfaite, d'inductance L et de résistance nulle. Dans cette partie du problème, la résistance de l'induit du moteur est négligée ; on peut donc considérer que la valeur moyenne de la tension d'induit est égale à la force électromotrice du moteur <uM> =E=kn avec k = 0,45 V s tr-1. Qu'appelle t-on un hacheur, quelle est sa fonction ? Le hacheur série est un convertisseur continu - continu . Alimenter l'induit du moteur par l'intermédiaire d'un hacheur permet d'obtenir une tension continue réglable aux bornes de l'induit, donc de réguler la vitesse de rotation du moteur. Le transistor bipolaire est ici utilisé comme interrupteur électronique. Quel(s) autre(s) composant(s) pourrait-on employer à la place du transistor bipolaire ? diode, thyristor .  Le hacheur sert à transporter de l'énergie entre deux dispositifs que nous désignerons sous le terme générique "source". D'un côté le générateur de tension constante U0=24 V, source1, de l'autre la machine à courant continu, source 2. En le justifiant par des considérations énergétiques, montrer que la f.c.e.m du moteur ainsi que la tension à ses bornes sont continues ( au sens mathématique dt terme). La tension de sortie du hacheur n'est pas continue, mais toujours positive. Si la rériode est assez faible, la charge ( le moteur) ne voit pas les crénaux, mais la valeur moyenne de la tension. On considère, en raison du résultat précédent, que la source 2 est équivalente à un générateur de tension. Quelles sont les conditions qui permettent de connecter directement deux sources de tension ? Sont-elles vérifiées ici ? Les sources de tension doivent avoir la même f.e.m : condition non vérifiée ici. Quelle est la grandeur électrique continue ( au sens mathématique) au sein d'une inductance ? L'intensité du courant est une fonction continue. Expliquer pourquoi on peut connecter directement la source 1 et l'ensemble machine à courant continu + inductance. Le moteur doit être traversé par un courant de valeur la plus continue possible : l'inductance assure la continuité de l'intensité.  Ecrire la relation entre les valeurs instantanées des tensions u(t), uL(t) et uM(t).  u(t) = uL(t) + uM(t). Montrer que les valeurs moyennes des tensions u et uM sont égales. Pour un signal périodique la valeur moyenne de la tension aux bornes de l'inductance est nulle.<uL>=0. Par suite : <u> = <uM>. 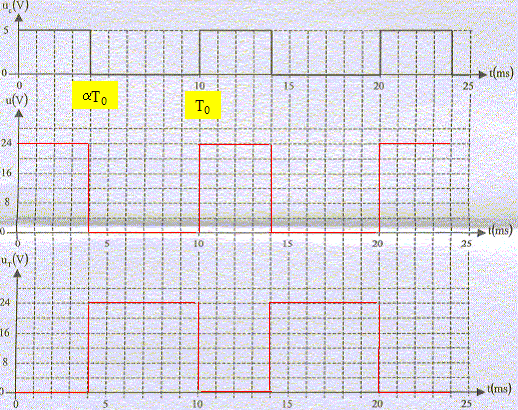La tension de commande uc(t) du transistor T est donnée ci-dessous. Déterminer la période T0 et le rapport cyclique a. T0 = 10 ms = 10-2 s ; a = 4/10 = 0,4. Compléter les chronogrammes en traçant les formes d'onde des tensions u(t) et uT(t).  Montrer que la valeur moyenne <u> de la tension délivrée par le hacheur est proportionnelle au rapport cyclique a. <u> = [ aT0 U0+(1-a) T0 *0] / T0 = aU0. En déduire que la fréquence de rotation n du moteur, exprimée en tr/s, peut s'écrire sous la forme n=ga. <u> =<uM> = aU0 ; de plus <uM> =E=kn avec k = 0,45 V s tr-1. D'où : aU0 = kn ; n = U0/ k a avec g = U0/ k Déterminer la valeur et l'unité de g. g = U0/ k; unité tr s-1 ; valeur 24/0,45 = 53 tr s-1. 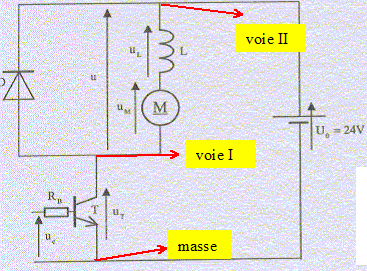On désire observer simultanément les tensions u(t) et uT(t) sur l'écran d'un oscilloscope. Indiquer les branchements des voies I et II et de la masse de l'appareil. u(t) = U0-uT ; il faut soustraire uT voie II : touche "ADD" et touche " opposée de la voie I". Préciser les valeurs choisies pour la base de temps ( ms/div) et les sensibilités ( V/div) sur les deux voies. La valeur maximale des tensions étant 24 V et l'écran mesurant 8 cm de haut : 5 V/div. La période est 10 ms et l'écran mesure 10 cm de large : 1 ms/div.

retour -menu