|
Loi de Kepler ; ester. Concours manipulateur électroradiologie médicale Nantes 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Données : Rayon terrestre 6370 km ; constante de gravitation G= 6,67 10-11 S.I ; g0 = 9,81 N /kg. Jour solaire : temps qui sépare deux passages successifs du soleil à la verticale d'un lieu : 24 heures. Jour sidéral : durée d'une rotation complète de la terre autour de son axe des pôles : 23 h 55 min 40 s. Une planète noté L possède trois satellites notés respectivementy A, B et C. On a reporté ci-dessous les périodes T et les rayons des orbites de ces satellites.
Parmi les propositions suivantes concernant un satellite géostationnaire, lesquelles sont vraies ? a). Sa période de révolution vaut T = 86400 s. Faux. Le satellite géostationnaire paraît fixe pour un observateur terrestre ; dans le plan équatorial, il tourne à la même vitesse angulaire que la terre et dans le même sens. Sa période est égal au jour sidéral soit 23*3600+55*60+40 =86140 s. b). Son altitude au dessus de la surface de la terre vaut z = 38600 km. Faux. altitude proche de 36 000 km. c). Il peut filmer ou photographier à tout moment la même région du globe terrestre. Vrai. Le satellite géostationnaire paraît fixe pour un observateur terrestre.
Utiliser la 3ème loi de Kepler
: T2/R3 =
4p2/(GM).
Calculer le champ gravitationnel crée par la planète L sur le satellite B considéré comme ponctuel ( en N/kg).
g = GM/ d2 . M= 8,83 1025 kg ; d= 192 106 m g = 6,67 10-11 *8,83
1025 / (192
106)2=
0,16 N
/kg.
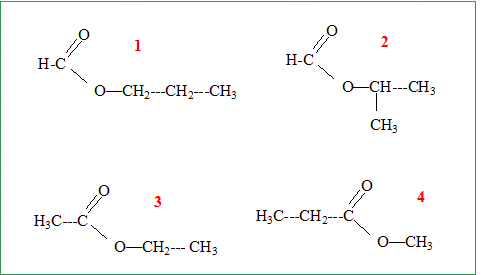
Un ester A a pour formule brute C4H8O2. Ecrire les formules semi développées de tous les esters ayant cette formule brute.
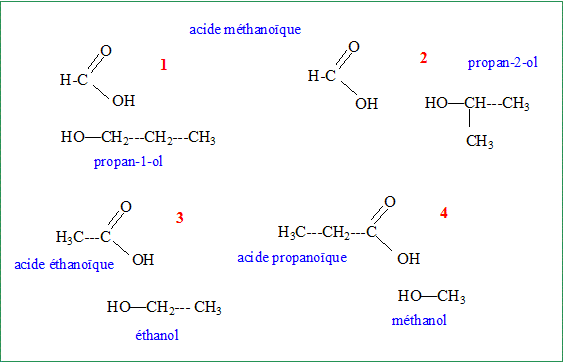
Préciser le nom et la formule de l'alcool et de l'acide que donne chacun des esters par hydrolyse.
Soit B l'acide carboxylique et C l'alcool utilisés pour la synthèse de A. Identifier A, B et C sachant que B peut être obtenu par oxydation ménagée de C. B et C comptent le même nombre d'atomes de carbone. C : éthanol ; B acide éthanoïque ; A est l'ester n°3 : éthanoate d'éthyle.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|