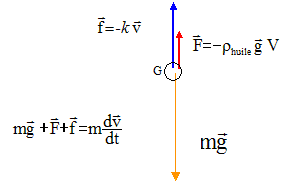Chute d'une bille dans deux liquides non miscibles concours kiné Nantes 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

On superpose dans une éprouvette deux liquides non miscibles : de l'huile de masse volumique rH= 0,92 g cm-3 et du sirop de grenadine de masse volumique rS = 1,20 g cm-3. Chaque colonne de liquide a une hauteur de 15 cm. On immerge totalement une petite bille d'acier de masse m dans l'huile, puis on la lâche sans vitesse initiale ; elle tombe alors verticalement. Les vecteurs sont écrits en gras et en bleu. On admet que dans les deux liquides, la force de frottement f est de la forme f = -kv ; k est le coefficient de frottement, il dépend de la viscosité de chacun des liquides et v est la vitesse du centre d'inertie de la bille. La masse volumique de l'acier est r=7,80 g cm-3 ; g = 9,81 m/s2. Effectuer l'inventaire des forces exercées sur la bille en mouvement ( faire un schéma). La bille est soumise à son poids, à la poussée d'Archimède et à la force de frottement.   En appliquant la seuxième loi de Newton montrer que l'équation différentielle se met sous la forme : dvz/dt = A-B vz où A et B sont des constantes. vz est la composante verticale de la vitesse sur un axe vertical orienté vers le bas.   Sur un axe vertical orienté vers le bas la seconde loi de Newton s'écrit, dans le cas de l'huile : mg - kvz - rHVg = mdvz/dt. avec m = r V, V étant le volume de la bille. r Vg - kvz - rHVg = r V dvz/dt ; on divise chaque terme par r V d'où : dvz/dt = g(1- rH/r) -k/(r V) vz. Calculer la valeur du coefficient A pour chaque liquide. Huile : A = g(1- rH/r) =9,81(1-0,92/7,80) =8,65m s-2. Sirop : A = g(1- rS/r) =9,81(1-1,2/7,80) =8,30m s-2. Le graphe ci-après donne vz(t) de la bille lorsqu'elle est dans l'huile. Déterminer la vitesse limite vl H de la bille dans l'huile. En déduire la valeur du coefficient BH. dvl H/dt = A-BH vl H = 0 soit BH = A/vl H = 8,65 / 0,4 = 21,6 s-1.   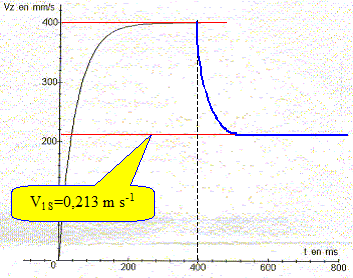A l'instant t = 400 ms la bille change de liquide. Le coefficient k du sirop est 1,8 fois plus important que celui de l'huile. Calculer la valeur du coefficient BS et la vitesse limite V l S atteinte dans le sirop de grenadine. kS=1,8 kH ; B=k/(r V) d'où BS=1,8 BH=1,8*21,6 ; BS= 38,9 s-1. AS-BS vl S = 0 soit vl S =AS/BS =8,30 / 38,9 ; vl S =0,213 m/s. Calculer les constantes de temps tH et t S des mouvements dans chacun des liquides. Donnée : (dx/dt + x/t = A avec t constante de temps et A une constante ) L'équation différentielle s'écrit :  dvz/dt +B vz = A. On identifie t à 1/B : tH =1/21,6 = 0,0463 s = 46,3 ms. tS =1/38,9 = 0,0257 s = 25,7 ms. Compléter le graphe ci-dessus en représentant vz entre 400 et 800 ms. 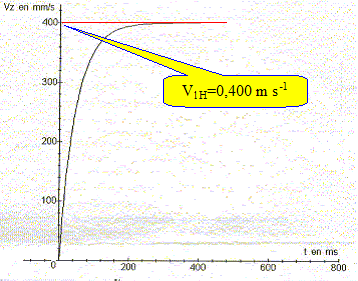Etablir les équations donnant l'expression de vz en fonction du temps dans l'huile et dans le sirop. Donnée : dx/dt + x/t = A avec t constante de temps et A une constant. Solution de cette équation x(t) = a exp(-t/t) + b où a et b sont des constantes. vz(t) = a exp(-t/t) + b. Dans l'huile : la vitesse initiale est nulle soit : 0 = a + b ; a =- b. si t devient très grand, la vitesse tend vers 0,4 m/s d'où : 0,4 = b. Par suite vz(t) = 0,4[1- exp(-t/0,0463) ] (1) Dans le sirop : vz(t) = a exp(-(t-0,4)/t) + b. Si t devient très grand, la vitesse tend vers 0,213 m/s d'où : 0,213 = b. La vitesse à t = 0,4 s est 0,4 m/s soit : 0,4 = a + 0,213 ; a =0,187 m s-1. Par suite vz(t) = 0,187exp(-(t-0,4)/0,0257) + 0,213. De quelle hauteur h par rapport à l'interface des deux liquides a t-on lâché la bille ? Primitive de (1) : z(t) = 0,4[ t +0,0463 exp(-t/0,0463)] + Cte. z(0) = 0,4*0,0463 + Cte = 0,0185 +Cte. La bille atteint la surface séparant les deux liquides à t = 0,4 s. 0,15 = 0,4[0,4+0,0463 exp(-0,4/0,0463)] + Cte. 0,15 = 0,4*0,4 + Cte d'où Cte = -0,01 m. Par suite z(0) = 0,0185-0,01 = 8,5 10-3 m = 0,85 cm par rapport à la surface libre de l'huile h = 15-0,85 = 14,1 cm par rapport à la surface de séparation des liquides.

retour -menu