Champ magnétique crée par un fil ; densimètre concours kiné Nantes 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

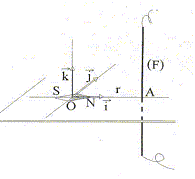
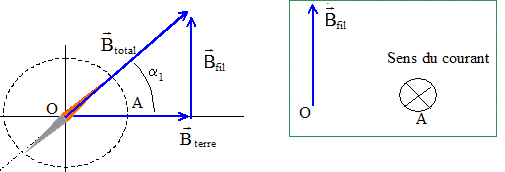
Un fil rectiligne infini, parcouru par un courant électrique I crée, en un point distant de r, un champ magnétique B = m0 I/(2pr) avec m0 = 4p 10-7 S.I. L'aiguille aimantée d'une boussole est orientée suivant l'axe (O i), la pointe nord N dans le sens de i. Un fil conducteur verticale très long F peut être déplacé autour de O sur une circonférence de rayon r = 10 cm. (F) est en A ( r,0, 0) lorsqu'on envoie un courant I0 = 10 A dans (F), l'aiguille aimantée tourne alors d'un angle a1 =(i , SN) =45° dans le plan horizontal. Préciser le sens du courant électrique dans (F). La boussole s'oriente suivant le champ magnétique total, somme vectorielle du champ magnétique terrestre et du champ crée par le fil. La règle de l'observateur donne le sens du courant, connaissant le sens du champ crée par le fil : le courant I descend le fil.   (F) étant toujours placé en A, on envoie dans le fil un courant de même sens mais d'intensité 2I0. 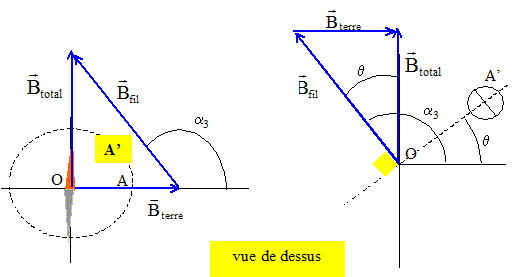Calculer l'angle a2. tana1 =tan 45 ° = 1 =B1 fil / Bterre d'où B1 fil = Bterre B1 fil = m0 I0/(2pr)   tan a2 =B 2 fil / Bterre = B 2 fil / B1 fil avec B2 fil = m0 2I0/(2pr) tan a2 =2 ; a2 = 63,4°. En quel point A', distant de OA'=r=10 cm du point O, doit-on placer (F) parcouru par le courant précédent I=2I0 pour que l'aiguille fasse un angle a3 = +90 °, c'est à dire s'orientant suivant j. On donnera la position de A' par l'angle q =(i, OA') et par ses coordonnées dans (O, i, j). sin q = Bterre / B 2 fil = B1 fil / B 2 fil = 0,5 ; q =30°. xA' = r cos 30 = 10 *0,866 = 8,67 cm. yA' = r sin 30 = 10 *0,5= 5 cm.   Un densimètre est constitué d'un flotteur de volume V0 surmonté d'une tige cylindrique de section s et de hauteur H. Le flotteur est lesté pour stabiliser l'appareil en position verticale. On plonge le densimètre, de mase M, dans un liquide de masse volumique m et on note h la hauteur immergée de la tige. 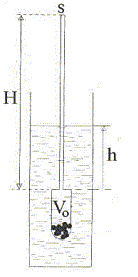Ecrire la condition d'équilibre du densimètre et établir la relation donnant m en fonction de M, V0, h et s. Le densimètre est en équilibre sous l'action de son poids ( valeur Mg) et de la poussée d'Archimède. Ces deux forces sont opposées et ont même valeur. Volume du densimètre immergé : V0+hs. Poussée d'Archimède = poids du volume de liquide déplacé : mg(V0+hs) d'où : Mg = mg(V0+hs) ; M = m(V0+hs) ; m = M/(V0+hs). Calculer V0 si dans l'eau h = 15,0 cm. M= 50,00 g ; s = 1,00 cm2 ; meau = 1000 kg m-3. V0+hs = M/m ; V0 = M/m- hs avec M = 0,05 kg ; s = 10-4 m2 ; h = 0,15 m. V0= 0,05/1000 -0,15 10-4 =3,50 10-5 m3 = 35,0 cm3.   On plonge le densimètre successivement dans deux liquides diférents ; les hauteurs immergées sont respectivement h1 = 19,3 cm et h2 = 6,7 cm. Calculer les densités d1 et d2 de ces liquides. g = 9,81 N/kg. m = M/(V0+hs) m1 =0,05 / (35 10-6 + 0,193 10-4) =921 kg m-3 = 0,921 g cm-3 ; d1 = 0,921. m2 =0,05 / (35 10-6 + 0,067 10-4) =1,20 103 kg m-3 = 1,20 g cm-3 ; d2 = 1,20.

retour -menu