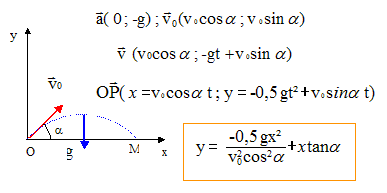Fronde, dipôle RLC, circuits dérivés.

Concours Officier 1ère classe de la Marine Marchande 08

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

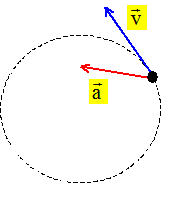
La fronde est une arme de jet constituée d'une pièce de matière souple attachée à deux lanières dans laquelle est placé le projectile. En faisant tourner cet ensemble autour de lui, le frondeur apporte une énergie cinétique importante au projectile ; lorsqu'il lâche les deux lanières le projectile s'échappe de la fronde.

Dans tout le problème le projectile est assimilé à un point matériel de masse m= 450 g et on négligera tous les frottements ; g = 9,8 m s^-2.

Le projectile est dans la fronde et on admet que sa trajectoire est un cercle de rayon r = 1,2 m

Représenter sur un schéma la trajectoire du projectile, l'allure des directions et le sens de son vecteur vitesse et de son vecteur accélération lorsque la vitesse de rotation de la fronde s'accroît.

Le vecteur vitesse a toujours le sens du mouvement est sa direction est la tangente au cercle au point considéré.

Le vecteur accélération n'est pas centripète car la valeur de la vitesse s'acroît.

Le projectile tourne maintenant à vitesse constante de 1,5 tr/s.

Calculer les valeurs suivantes se rapportant au projectile :

vitesse V : vitesse angulaire w = 1,5*2p = 3 p radian/s.

vitesse V = w r = 3*3,14*1,2 = 11,3 m/s ~11 m/s.

accélération a : accélération centripète a = V²/r = 11,3²/1,2 = 1,06 10² m/s²~ 1,1 10² m/s².

énergie cinétique Ec : Ec = ½mV2 = 0,5*0,45*11,32 =28,7 J ~ 29 J.

 

Lorsque le frondeur lâche une des lanières, le projectile est libéré en un point repèré O avec une vitesse initiale v0 de valeur 11,3 m/s, dirigée vers le haut et faisant un angle a=30 ° avec le plan horizontal. Le projectile tombe sur le sol en un point appelé A situé à une altitude plus basse de 3 m que le point O. A l'aide de la deuxième loi de Newton montrer que la trajectoire du projectile se situe dans un plan vertical. Le projectile n'est soumis qu'à son poids, verticale vers le bas : la deuxième loi de Newton indique que l'accélération est le champ de gravitation g. De plus la vitesse initiale v0 est dans un plan vertical. Le mouvement est dans le plan défini par le vecteur accélération et le vecteur vitesse initiale : c'est à dire le plan vertical. Etablir les équations horaires du mouvement du projectile dans le plan vertical en prenant le repère (O i j ). Etablir l'équation cartésienne de la trajectoire. indiquer le nom donné à cette trajectoire. La trajectoire est une branche de parabole. En déduire le type de mouvement suivant l'axe Ox puis suivant l'axe Oy. Mouvement uniforme suivant Ox à la vitesse v0 cos a ; Mouvement uniformément accéléré suivant Oy. Calculer l'altitude maximale y maxi atteinte par le projectile. Au sommet de la parabole le vecteur vitesse est horizontal ; sa composante verticale est nulle. 0 = -gt + v0 sin a ; t = v0 sin a / g. repport dans l'expression de y : ymaxi = -0,5 g (v0 sin a / g)2 + v0 sin a v0 sin a / g. ymaxi = (v0 sin a)2 / (2g) = (11,3*sin 30)2/19,6 =1,63 m ~ 1,6 m.

Abscisse x_A du point d'impact sachant que y_A= -3 m.

-3 = -0,5*9,8 x²_A /( 11,3 cos 30)² + x_A tan 30 ; -3 = -0,051 x²_A + 0,577 x_A.

x²_A -11,3 x_A - 58,8 = 0 ; D^½ =19,0 ; x_A = 15,2 m.

OA = (x²_A + y²_A )^½ =(15,2² + (-3)² )^½ =15,5 m.

Calculer le temps mis par le projectile pour aller de O à A.

x_A = v₀ cos a t soit t = x_A /( v₀ cos a) = 15,2 /(11,3 cos 30) = 1,55 s ~ 1,6 s.

Calculer la vitesse du projectile juste avant qu'il n'atteigne le point A.

v_x = v₀ cos a = 11,3 cos 30 =9,79 m/s ; v_y = -gt +v₀ sin a =-9,8*1,55 + 11,3 sin 30 = -9,54 m/s

v = (v²_x + v²_y )^½ =(9,79² + (-9,54)² )^½ =13,7 m/s ~14 m/s.

Calculer la valeur de l'angle b que fait le vecteur vitesse avec le plan horizontal juste avant d'atteindre A.

tan _b = |v_y|/v_x =9,54/9,79 =0,974 ; b = 44°.

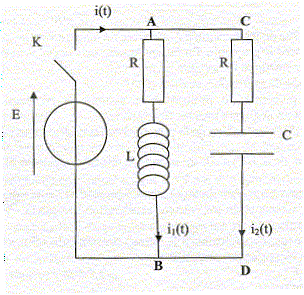
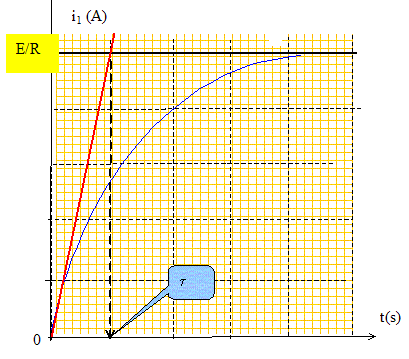
Le condensateur est initialement déchargé, on ferme l'interrupteur à t = 0 s.

Exprimer la tension U_AB aux bornes du dipôle RL en considérant la bobine comme idéale.

U_AB = Ri₁ + L di₁/dt = E

Etablir l'équation différentielle vérifiée par l'intensité du courant i₁.

di₁/dt +R/L i₁ =E/L. (1)

La solution de l'équation différentielle est de la forme i = a+b exp(-t/t) où a, b, t sont des constantes.

Déterminer a, b, t en fonction des paramètres du circuit. Donner l'expression de i₁(t) et l'allure de la courbe de variation de i₁(t) en fonction du temps.

di₁/dt = -b/t exp(-t/t)

repport dans (1) : -b/t exp(-t/t) +R/L a + R/L bexp(-t/t) =E/L

b(-1/t + R/L)exp(-t/t) +Ra/L=E/L.

Cette égalité est vérifiée quel que soit le temps si : t = L/R et si a = E/R.

De plus à l'instant initial i₁(0) = 0 = a+b soit b=-a ; b= -E/R

par suite i₁(t) = E/R (1- exp(-t/t).

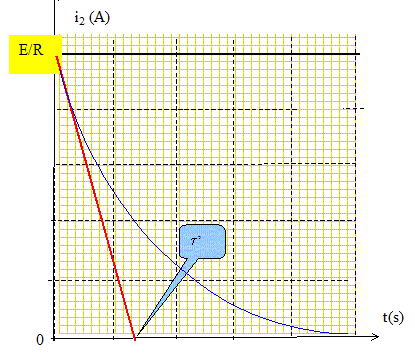
U_CD = Ri₂ + u(t) = E avec u(t) tension aux bornes du condensateur.

Etablir l'équation différentielle vérifiée par la tension u(t) aux bornes du condensateur.

Ri₂ + u(t) = E avec i₂ = dQ/dt et Q = Cu(t) soit i₂(t) = Cdu(t)/dt.

RCdu(t)/dt + u(t) = E (2)

La solution de l'équation différentielle est de la forme u = a'+b' exp(-t/t') où a', b', t' sont des constantes.

Déterminer a', b', t' en fonction des paramètres du circuit. Donner l'expression de u(t), en déduire l'expression de i₂(t) et l'allure de la courbe de variation de i₂(t) en fonction du temps.

du/dt = -b'/t' exp(-t/t')

repport dans (2) : -RCb'/t' exp(-t/t) + a + b exp(-t/t') =E

b'(-RC/t' +1)exp(-t/t') +a=E.

Cette égalité est vérifiée quel que soit le temps si : t' = RC et si a' = E.

De plus à l'instant initial u(0) = 0 = a'+b' soit b=-a' ; b'= -E

par suite u(t) = E (1- exp(-t/t').

i₂(t) = Cdu(t)/dt = CE/t'exp(-t/t') ; i₂(t) = E/R exp(-t/t').

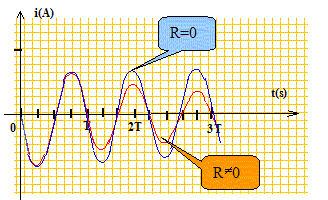
Après un temps suffisamment long pour que le régime permanent soit établi, on ouvre l'interrupteur K. On prend cet instant comme nouvelle origine des temps.

Etablir l'équation différentielle vérifiée par la tension u(t) aux bornes du condensateur. Etudier le cas où les résistances R sont négligeables.

2Ri + Ldi/dt + u =0 avec i = dq/dt = Cdu/dt , di/dt = Cd²u/dt²

par suite LC d²u/dt² +2RCdu/dt + u = 0.

Si R est négligeable : LC d²u/dt² + u = 0. (3)

du/dt = -U_m w sin (wt+j) ; d²u/dt² = -U_m w² cos (wt+j)

repport dans (3) : -LCU_m w² cos (wt+j) + U_m cos (wt+j) =0

égalité vérifiée quel que soit le temps si w² = 1/(LC).

A l'instant t=0, le condensateur est chargé u=E d'où : E= U_m cos j soit U_m =E et cos j = 1 ( j =0).

Déduire de l'expression de u(t) celle de l'intensité i(t). Donner l'allure de la courbe de variation de i(t) en fonction du temps. Donner l'allure de la courbe si R n'est plus négligeable.

i(t) = Cdu/dt = -CE w sin (wt).