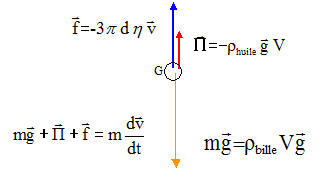Onde ultraonore ; planète Pluton ; chute verticale ; diffraction.

Concours Officier 1ère classe de la Marine Marchande 08

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

La quille d'un navire est équipée d'un sondeur acoustique comportant un émetteur et un récepteur d'onde ultrasonore de fréquence f = 200 kHz.

L'émetteur envoie des salves d'ultrasons verticalement en direction du fond à des intervalles de temps réguliers. L'onde sonore se déplace à célérité constante "v" et est réfléchie en partie vers le récepteur lorsqu'elle rencontre un obstacle. La mesure du retard entre l'émission et la réception permet de calculer la profondeur d'eau "h" sous la quille.

Pour cette question on prendra v = 1500 m/s.

Indiquer si l'onde ultrasonore est une onde longitudinale ou transversale. Justifier.

Les ondes ultrasonores sont des ondes mécaniques progressives longitudinales.( propagation d'une variation de pression)

La direction de propagation de l'onde et la direction de la propagation des variations de pression sont identiques.

Exprimer la durée Dt₁ séparant le début de l'émission de la salve, au début de la réception de son écho en fonction de h et v.

Aller + retour =2 h = v Dt₁ ; Dt₁ = 2h/v.

La durée de la salve émise est de 5 ms.

Calculer la profondeur minimale h_mini pour que la durée Dt₂ séparant la fin de l'émission de la salve et le début de la réception de l'écho ne soit pas nulle.

Si Dt₁= 5 10^-3 alors Dt₂ =0.

h_mini = ½v Dt₁ = 2,5 10^-3*1500 = 3,75 m.

On veut pouvoir mesurer des profondeurs jusqu'à 250 m avec cet appareil.

Dans ces conditions, calculer la durée Dt₃ entre les débuts de salves émises pour que la réception de l'écho d'une salve s'effectue toujours avant l'envoi de la salve suivante.

Dt ₃= 2h/v = 2*250/1500 = 1/3 =333 ms.

Planète Pluton. (3 pts) On considère une planète P en orbite circulaire autour du soleil S, centré en O, supposé fixe. On note m la masse de la planète, M la masse du soleil et R le rayon de l'orbite. Indiquer la condition sur m et M pour que l'hypothèse "O fixe "soit valable. Le barycentre des deux masses doit être pratiquement confondu avec le centre du soleil. Cela est possible si la masse M du soleil est bien supérieure à la masse m de la planète. m<< M.

 

Indiquer ce que représente en fait le point P. Préciser dans quel référentiel est étudié le mouvement. Le poit P représente le centre de la planète. Le mouvement de P est étudié dans le référentiel héliocentrique. Donner l'expression de la vitesse linéaire de P en fonction de R, M et G, constante de gravitation. v = [GM / R]½ avec M en kg, R en m. Donner l'expression de la vitesse angulaire w de P. En déduire l'expression de la période de révolution de P autour du soleil. v = wR soit w = v/R ; w =[GM / R3]½, exprimée en rad s-1. De plus la période T est égale à : T = 2p/w. T = 2p[R3/(GM )]½. (1) La loi de Kepler affirme que T2/R3 = constante. Donner l'expression de cette constante en fonction de G et M. Elever l'expression (1) au carré : T2 = 4 p2 R3/(GM) soit T2 /R3 = 4 p2/(GM). La planète Pluton, découverte en 1910, se trouve à une distance de 40 U.A du soleil ( où U.A, unité astronomique est la distance Terre Soleil ). Récrire la loi de Kepler dans le système d'unités ( années terrestres ; unités astronomiques). Montrer quelle prend une forme particulièrement simple. T2terre / R3terre = T2pluton / R3pluton T2pluton /T2terre = R3pluton / R3terre ; [ Tpluton /Tterre ]2 =[Rpluton / Rterre ]3.   Tpluton et Tterre doivent être dans la même unité ( par exemple année terrestre) Rpluton et Rterre doivent être dans la même unité ( par exemple U.A). Tterre = 1 an ; Rterre = 1 U.A d'où : T2pluton =R3pluton. Déterminer si la planète Pluton a décrit entièrement son orbite depuis sa découverte. Sinon exprimer en % la fraction parcourue depuis sa découverte. Rpluton = 40 U.A ; Tpluton = 403/2 = 253 ans. 2008-1910 = 98 ans. Pluton n'a pas encore décrit entièrement son orbite ; Pluton a seulement décrit 98/253*100 =38,7% de son orbite.

Pour déterminer la viscosité h d'une huile, on dispose d'un tube cylindrique transparent de 30 cm de haut et de 3 cm de diamètre et d'une bille de 5 mm de diamètre.La force de frottement fluide est de la forme f=-kv, expression dans laquelle v est la vitesse et k un coefficient tel que k = 3p h d, d étant le diamètre de la bille.

A l'instant t=0, on lâche la bille sans vitesse initiale du haut du tube que l'on à rempli avec l'huile à tester.

Lorsque la bille passe en face du premier repère gradué 10 cm sous le niveau d'huile, on met en route le chronomètre. Lorsqu'elle passe en face du deuxième repère gradué 25 cm sous le niveau d'huile, on arrête le chronomètre. La durée de la chute de la bille entre les deux repères est Dt = 7,5 s.

On donne : masse volumique de la bille : m_bille = 7800 kg m^-3 ; masse volumique de l'huile : m_huile= 900 kg m^-3 ;

g = 9,8 m s^-2 ; volume V de la bille V = pd³/6.

Indiquer les forces auquelles la bille est soumise pendant son mouvement dans l'huile ; les représenter sur un schéma.

Poids, vertical, vers le bas, valeur mg = V m_billeg = pd³/6 m_billeg

Poussée d'Archimède, verticale, vers le haut, valeur Vm_huileg = pd³/6 m_huileg

Force de frottement fluide , verticale, vers le haut, valeur 3p h d v

Etablir l'équation différentielle du mouvement liant la vitesse v et sa dérivée par rapport au temps.

pd³/6 m_billeg - pd³/6 m_huileg -3p h d v = pd³/6 m_bille dv/dt

d²/6 m_billeg -d²/6 m_huileg -3 h v = d²/6 m_bille dv/dt

dv/dt + 18 h / ( m_bille d²) v = ( 1-m_huile/m_bille)g. (2)

Calculer la valeur de cette vitesse.

Distance des repères / Dt = 0,15 / 7,5 ; v_lim =0,02 m/s.

Définir le type de mouvement de la bille entre les deux repères.

La valeur de la vitesse est constante ; le mouvement est rectiligne : mouvement rectiligne uniforme.

Calculer la valeur du coefficient k de la force de frottement fluide.

d v_lim/dt =0 ; (2) donne : v_lim = (1-m_huile/m_bille) g ( m_bille d²)/ ( 18 h).

v_lim = (m_bille-m_huile) g d²/ ( 18 h) = (m_bille-m_huile) g p d³/ (6*3p hd) ; Or k = 3p h d

v_lim = (m_bille-m_huile) g p d³/ (6k) ; k = (m_bille-m_huile) g p d³/(6 v_lim).

k = (7800-900)*9,8*3,14*(5 10^-3)³ / (6*0,02) =0,22 kg s^-1.

Déterminer la dimension de la viscosité h de l'huile. Calculer sa valeur en précisant l'unité utilisée.

k = 3p h d d'où h = k/( 3p d)

3p est sans dimension ; d est une longueur [d]= L ; [k] = M T^-1 d'où [h]= M T^-1 L^-1.

unité de h : kg m^-1 s^-1 = kg m s^-2 m^-2 s = N m^-2 s = Pa .s

h = 0,22 / (3*3,14 *5 10^-3) = 4,7 kg m^-1 s^-1 = 4,7 Pa s.

Calculer la valeur de T à partir de l'équation différentielle établie précédemment.

dv/dt + 18 h / ( m_bille d²) v = ( 1-m_huile/m_bille)g. (2)

Multiplier chaque terme par m_bille : m_bille dv/dt + 18 h / ( d²) v = ( m_bille -m_huile)g.

Multiplier chaque terme par p d³/ (6k) : m_bille p d³/ (6k) dv/dt + 3p h d / k v = ( m_bille -m_huile)gp d³/ (6k).

m_bille p d³/ (6k) dv/dt + v = v_lim.

On identifie T à m_bille p d³/ (6k).

T = 7800*3,14*0,005³ /(6*0,22) =2,3 10^-3 s.

Calculer le temps au bout duquel v = 0,98 v_lim ; en déduire que lorsque la bille passe devant le premier repère, sa vitesse est supérieure à cette valeur.

0,98 v_lim = v_lim( 1-exp(-t/T)) ; 0,98 = 1-exp(-t/T) ; exp(-t/T) =0,02 ; -t/T = ln 0,02 =-3,9

t = 1,7 T = 3,9*2,3 10^-3 = 9,0 10^-3 s.

La constante de temps T étant de l'ordre de 2 ms, la vitesse limite est très rapidement atteinte : lorsque la bille passe devant le premier repère la vitesse limite est atteinte.

Calculer la valeur de la tangente à l'origine de v(t) ; indiquer pour quelle valeur de t cette tangente coupe la droite d'équation v = v_lim.

v(t) = v_lim( 1-exp(-t/T)) ; dv(t) / dt = v_lim/T exp(-t/T) ; [ dv(t) / dt]₀ = v_lim/T = 0,02 / 2,3 10^-3 =8,7 m s^-2.

Cette tangente coupe la droite d'équation v = v_lim à t=T.

Représenter graphiquement l'allure de la courbe v(t). Indiquer sur le graphique les valeurs remarquables et les différentes zones du régime.