Mécanique de Newton, stimulateur cardiaque : radioactivité, condensateur : allumage. Marine marchande 07

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

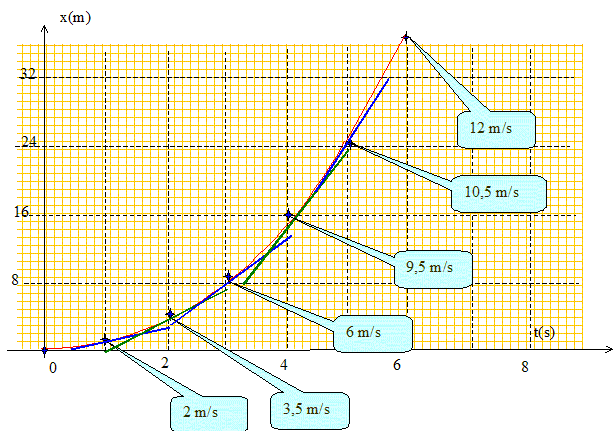
Une voiture de masse M = 980 kg se déplace sur une route horizontale rectiligne. Elle est soumise :

- à une action motrice, modélisée par un vecteur force F_m, parallèle à la route,

d’intensité constante F_m = 2800 N, appliquée au centre d’inertie ;

- à une action résistante, modélisée (tant que la vitesse est inférieure à 72 km.h^-1) par un vecteur force F_f d’intensité inconnue mais constante, de sens opposé à celui du déplacement et appliquée au centre d’inertie de la voiture.

Le tableau suivant donne les positions successives «x» de la voiture en fonction du temps «t» durant la phase où sa vitesse est inférieure à 72 km.h^-1 :

t(s)	0	1	2	3	4	5	6	7
x(m)	0	1	4	9	16	25	36	49

Indiquer une méthode pour évaluer la vitesse de la voiture à une date t donnée.

Tracer la courbe d'équation x=f(t) ; tracer les tangentes à cette courbe aux dates t demandées.

Le coefficient directeur de cette tangente est égal à la valeur de la vitesse à la date t.

Donner dans un tableau les valeurs de la vitesse aux dates 1s, 2s,…, 6s.

Les valeurs du tableau ci-dessus indiquent que x = t² ; d'où dx/dt = v = 2t.

t(s)	0	1	2	3	4	5	6	7
x(m)	0	1	4	9	16	25	36	49
v(m/s)	0	2	4	6	8	10	12	14

Valeurs en accord avec les valeurs déterminées graphiquement

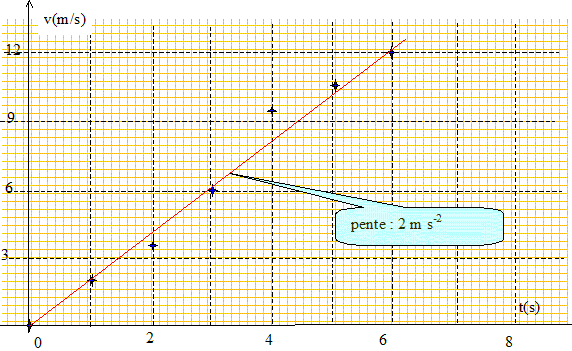
Représenter graphiquement les variations de cette vitesse v en fonction du temps t. 

Déterminer l’équation de la courbe v(t).

v= 2t.

Déduire de cette étude la valeur de l’accélération du mouvement.

L'accélération est la dérivée de la vitesse par rapport au temps : a = 2 m/s².

En déduire la valeur de la force F_f.

La seconde loi de Newton écrite sur un axe horizontal orienté dans le sens du mouvement donne :

F_m-F_f = Ma soit F_f = F_m-Ma.

F_f =2800-980*2 = 840 N.

La radioactivité.

Un stimulateur cardiaque contient une masse m = 130 mg de l’isotope 238 de plutonium Pu qui émet un rayonnement a lors de sa désintégration et dont la demi-vie vaut t_1/2 = 87,8 ans.

L’énergie libérée lors de chaque désintégration permet au stimulateur de produire del’électricité.

On donne un extrait de la classification des éléments : ₉₀Th, ₉₁Pa, ₉₂U, ₉₄Pu, ₉₆Cm, ₉₈Cf.

La masse molaire atomique du plutonium vaut M = 238 g.mol^-1. La constante d’Avogadro a pour valeur N = 6,02 10²³ mol^-1.

Définir ce qu’est la demi-vie.

Durée au bout de laquelle l'activité initiale est divisée par deux.

Définir ce qu’est un isotope.

Deux isotopes ne se différentient que par leur nombre de neutrons. Ils ont le même numéro atomique Z.

Préciser comment s’appelle le phénomène de désintégration du plutonium.

Radioactivité de type a, émission d'un noyau d'hélium. ( fission d'un gros noyau instable )

Définir ce qu’est l’activité A et à quoi correspond le Becquerel.

L'activité est le nombre de désintégrations par seconde.

1 Bq = 1 désintégration en 1 seconde.

Ecrire la réaction de désintégration du plutonium 238. Préciser quels sont les rayonnements émis lors de la désintégration si le noyau fils est émis dans un état excité.

²³⁸₉₄Pu --> ^A_ZX* +⁴₂He

Conservation de la charge : 94 = Z+2 soit Z = 92, élément uranium

Conservation du nombre de nucléons : 238=A+4 soit A = 234

²³⁸₉₄Pu -->²³⁴₉₂U* +⁴₂He (noyau d'hélium)

²³⁴₉₂U* -->²³⁴₉₂U + g ( photon g, de même nature que la lumière)

Calculer le nombre de noyaux N₀ initialement présents dans le stimulateur et en déduire l’activité initiale A₀ de ce stimulateur.

Quantité de matière (mol) = masse (g) / masse molaire (g/mol)

n = m/M = 0,130/238 =5,4162 10^-4 mol

N₀ = n N = 5,4162 10^-4 *6,02 10²³ = 3,29 10²⁰ noyaux.

Constante radioactive l = ln2/t_½ avec t_½ =87,8 ans = 87,8*365*24*3600 =2,769 10⁹ s.

l = 0,693 / 2,769 10⁹ =2,50 10^-10 s^-1.

A₀ = l N₀ = 2,50 10^-10 *3,29 10²⁰ =8,23 10¹⁰ Bq.

Donner la loi de décroissance de l’activité en fonction du temps. Tracer la courbe représentative de cette loi lorsque t varie de 0 à 100 ans.

A = A₀ exp(-lt)  = A₀ exp(-7,89 10^-3 t)  avec t en années.

t(an)	0	20	40	60	80	100
A(Bq)	8,24 1010	7,04 1010	6,00 1010	5,13 1010	4,38 1010	3,74 1010

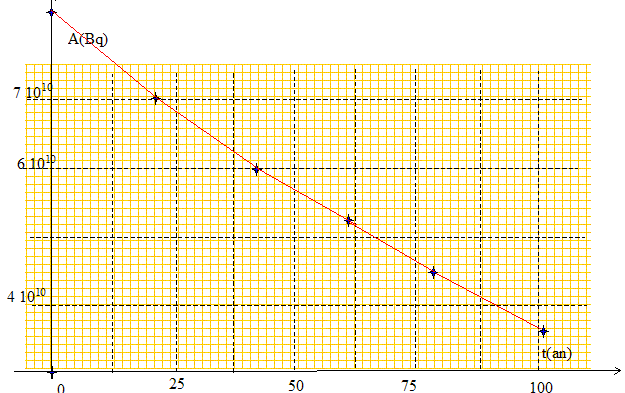
Le stimulateur fonctionne correctement jusqu’à une diminution de 30% de son activité.

Calculer sa durée de fonctionnement normal dans ces conditions et le nombre de noyaux N de plutonium restant à la fin de cette durée.

A_fin =0,7 A₀ ; A/ A₀ = exp(-lt)  ; ln 0,7 = -lt ; lt = 0,3567 ; l = 0,693/87,8 =7,8946 10^-3 an^-1.

t = 0,3567 / 7,8946 10^-3 = 45 ans.

A=lN ; A = 0,7 A₀ =0,7 lN₀ d'où N= 0,7 N₀ = 0,7*3,29 10²⁰ = 2,30 10²⁰.

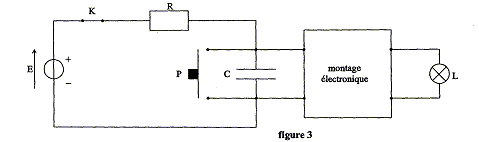
Le boîtier électronique M commande l’allumage de la lampe L lorsque la tension aux bornes du condensateur est inférieure à 20 volts. On admettra que ce boîtier ne consomme aucun courant provenant de R ou de C. On donne : E = 24 volts, R = 1500 kW, C = 100 µF.

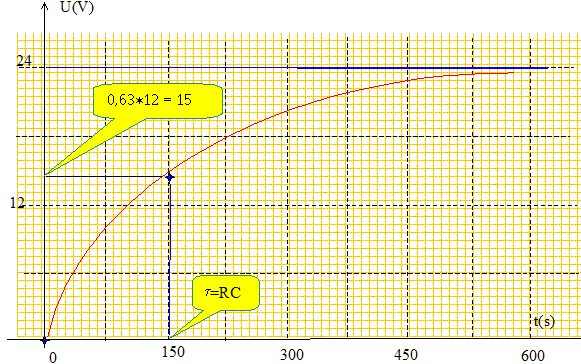
A l’instant t = 0, le condensateur C est complètement déchargé et le poussoir P est dans la position représentée sur la figure. A partir de l’équation différentielle de la tension u aux bornes du condensateur en fonction du temps, établir la relation : u = E(1 – exp(-t/RC)).

Additivité des tensions : E = Ri + u

De plus i = dq/dt et q=Cu soit dq/dt = Cdu/dt ; q étant la charge de l'armature supérieure du condensateur.

D'où : E = RCdu/dt + u ; du/dt + 1/(RC) u = E/(RC) ( équation différentielle (1))

Solution générale de l'équation sans second membre : u = Aexp(-t/(RC))

Solution particulière de (1) : u= E ( condensateur chargé)

Solution générale de (1) : u = Aexp(-t/(RC)) +E

0 t=0, le condensateur est déchargé : u(0)=0 d'où 0= A+E soit A=-E.

Par suite u= E(1-exp(-t/(RC)).

A partir des unités de t, R et C, montrer que t/(RC) est sans dimension.

Energie Joule : E = RI²t =U²/R t ; R = U² t / E

Energie stockée dans le condensateur E = ½CU² ; C = 2E / U²

Par suite RC a la dimension d'un temps et t/(RC) est sans dimension.

Représenter l’allure de l’évolution de la tension u aux bornes de C en fonction du temps. Indiquer sur votre graphe les valeurs caractéristiques.

Expliquer pourquoi la lampe s’allume lorsqu’on appuie sur le poussoir P.

On appuie sur le bouton poussoir P : on provoque la décharge instantanée du condensateur et u s'annule.

Or la lampe s'allume lorsque la tension u aux bornes du condensateur est inférieure à une valeur limite u_al =20 V : donc la lampe s'allume.

Calculer le temps pendant lequel la lampe reste allumée après qu’on ait relâché le poussoir P.

La lampe reste allumée tant que la tension u est inférieure à 20 V.

u= E(1-exp(-t/(RC)) ; 20 = 24 (1-exp(-t/150)) ; 1-20/24 = exp(-t/150) ;

0,1667 = exp(-t/150) ; ln0,1667= -t/150 ; t = 269 s.

En justifiant vos réponses, indiquer sur quels paramètres on peut jouer et dans quel sens on doit faire varier ces paramètres pour

obtenir le résultat voulu.

La tension E est constante ; la tension d'allumage est constante.

La durée d'allumage est proportionnelle au produit RC : en diminuant la capacité ou la résistance R, la durée d'allumage sera plus petite.