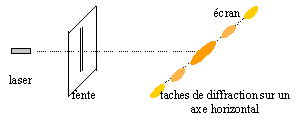Onde sonore ( Doppler) ; énergie mécanique ; ressort en rotation ; diffraction. Marine marchande 07

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

Pour cette question, on donne la vitesse de propagation du son dans l’air : v = 340 m.s^-1.

Le klaxon d’une automobile à l’arrêt émet un son dont la fréquence est de 500 Hz.

Indiquer le type d’onde auquel appartient le son.

Les ondes sonores sont des ondes mécaniques progressives longitudinales.( propagation d'une variation de pression)

Donner la relation qui lie fréquence, longueur d’onde et célérité ; calculer la longueur d’onde du son du klaxon.

l= c/f : l longueur d'onde (m) ; c : célérité (m/s) ; f : fréquence (Hz)

l = 340/500 = 0,68 m.

Un observateur est placé à 150 m de l’automobile.

Calculer l’intervalle de temps qui s’écoule entre le moment où le klaxon commence à retentir et celui où l’observateur commence à entendre le klaxon.

Dt = distance /célérité = 150 /340 = 0,44 s.

La voiture se déplace en direction d’un autre observateur à la vitesse de 40 km.h^-1 (en se rapprochant de lui). La distance entre voiture et observateur est de 150 m lorsque le klaxon de la voiture commence à retentir.

Indiquer si l’intervalle de temps qui s’écoule entre le moment où le klaxon commence à retentir et celui où l’observateur commence à entendre le klaxon a la même valeur qu’à la question précédente. Justifier.

Dt = distance /( célérité - vitesse de la voiture) ; v_em = 40/3,6 =11,1 m/s ;

Dt = 150/(340-11,1) = 0,456 s = 0,47 s.

Calculer la fréquence du son perçu par l’observateur. Préciser le nom donné à ce phénomène.

f = f_em / [ 1- v_em/c].

f_em : fréquence du klaxon émetteur( Hz) ; v_em : vitesse de la voiture (m/s) ; c : célérité du son dans l'air (m/s).

v_em = 40/3,6 =11,1 m/s ; f = 500 /[1-11,1/340]= 517 Hz ( son plus aigu)

Ce phénomène porte le nom d'effet Doppler.

Energie mécanique. Un solide S, de masse m = 0,15 kg, est attaché à l’extrémité d’un ressort horizontal à spires non jointives, de constante de raideur k = 10 N.m-1. Ce solide glisse sur une tige horizontale graissée et on négligera donc les frottements entre la tige et le solide. Le solide est écarté de 5 cm de sa position d’équilibre, dans le sens de l’allongement du ressort, puis il est lâché sans vitesse initiale à la date t = 0.

Calculer l’énergie cinétique du solide à la date t = 0.

Le solide étant lâché sans vitesse initiale, l'énergie cinétique initiale est nulle.

Calculer l’énergie potentielle élastique du système à la date t = 0.

E_pe = ½kx² avec x = 0,05 m et k = 10 N/m.

E_pe = 0,5*10*0,05² = 1,25 10^-2 = 1,3 10^-2 J.

Calculer l’énergie mécanique de l’oscillateur ainsi constitué.

L'énergie mécanique E_M est la somme de l'énergie cinétique et de l'énergie potentielle : E_M= 1,3 10^-2 J.

Indiquer ce que l’on peut dire de l’évolution de l’énergie mécanique au cours du mouvement.

En absence de frottement, l'énergie mécanique est constante.

Calculer la vitesse du solide lors du passage par la position d’équilibre du ressort. Au passage à la position d'équilibre, le ressort n'est pas déformé : x=0 L'énergie potentielle élastique est nulle ; l'énergie mécanique est sous forme cinétique : EM = ½mv2 ; v = [2EM/m]½. v = [2,5 10-2 / 0,15]½ =0,41 m/s.

L’ensemble tige, ressort, solide tourne autour d’un axe vertical à la vitesse constante de 1 tour par seconde de telle façon que le solide S décrit un cercle de rayon R = L + x, expression dans laquelle L est la distance entre l’axe de rotation et la position du solide au repos et x l’allongement du ressort.

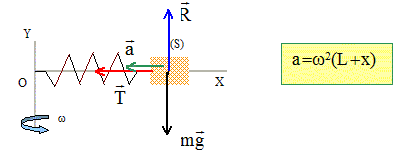
On donne L = 10 cm et le solide est assimilé à une masse ponctuelle.

Donner la direction et l’expression du vecteur accélération que subit le solide.

Donner l’expression de la force F due à l’allongement du ressort.

La seconde loi de Newton écrite sur l'axe horizontal donne : T = m w²(L+x) = kx.

Calculer l’allongement x du ressort.

w = 1 tour /s = 2 p = 6,28 rad /s ; m = 0,15 kg ; L= 0,10 m ; k = 10 N/m.

m w²(L+x) = kx ; x = m w²L / [k- m w² ] ;

x = L [ k/(m w²)-1].

x = 0,1 / [10/0,15*6,28²)-1] =0,145 m = 0,14 m.

Pour toute cette question, on prendra comme valeur de la vitesse de la lumière dans l’air et dans le vide : c = 3,00 10⁸ m.s^-1.

Définir le phénomène de diffraction.

Lorsque un faisceau de lumière monochromatique rencontre un obstacle, ou une fente, dont les dimensions sont de l'ordre de la longueur d'onde de cette lumière, on observe une tache centrale brillante et, de part et d'autre, une alternance de taches sombres et de moins en moins brillantes.

Un rayon laser, de longueur d’onde dans le vide l= 633 nm, traverse une fente de largeur" a ". On observe la figure de diffraction sur un écran placé perpendiculairement au rayon laser et à une distance D = 3,52 m de la fente.

Calculer la fréquence du rayon laser.

f = c/l avec l = 633 10^-9 m

f = 3,00 10⁸ / 633 10^-9 = 4,74 10¹⁴ Hz.

Tracer le schéma donnant l’aspect de la figure de diffraction.

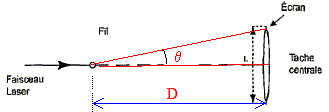
On mesure sur la figure de diffraction la distance «d₁» séparant le milieu de la frange centrale et l’apparition de la première extinction : d₁ = 46 mm.

Calculer la valeur de la largeur «a₁» de la fente utilisée.

tan q = ½L/D voisin de q radian pour les angles petits.

d'autre part q = l/a₁.

avec : l longueur d'onde (m) et a₁ : largeur de la fente (m)

2l/a₁=L/D soit a₁=2lD/ L où L représente "d₁".

a₁=2* 633 10^-9*3,52 / 46 10^-3 = 9,7 10^-5 m.

En utilisant d’autres fentes, les distances séparant le milieu de la frange centrale et le milieu de la première extinction ont pour valeur :

d₂ = 23 mm et d₃ = 15 mm.

Calculer les valeurs des largeurs des fentes correspondantes.

a₂=2* 633 10^-9*3,52 / 23 10^-3 = 1,9 10^-4 m.

a₃=2* 633 10^-9*3,52 / 15 10^-3 = 3,0 10^-4 m.

Donner une conclusion à propos de l’étalement des taches de diffraction.

La tache centrale est d'autant plus large que la largeur de la fente est plus faible.

La fréquence caractérise une onde. La fréquence est constante quel que soit le milieu de propagation.

Calculer l’indice de réfraction d’un morceau de verre si la célérité du rayon laser dans celui-ci a pour valeur c’ = 2,07 10⁸ m/s.

n = c/c' = 3,00 / 2,07 = 1,45.