Aurélie 17/01/08
 

Dipôle RL, Marine marchande 06

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts
. .
.
.

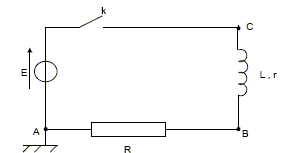
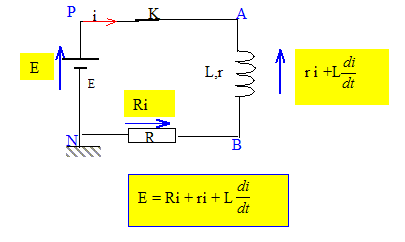
On considère le circuit série ci-dessous composé d’un générateur de f.e.m E, d’une bobine d’inductance L et de résistance r, d’un interrupteur K et d’une résistance R. L’interrupteur est fermé à l’instant t = 0 s.

Exprimer la relation entre E, L, r, R, i et di/dt.

Additivité des tensions :

Déduire de cette relation, une expression littérale de i(t).

di/dt + (R+r)/L i = E/L; on pose t = L/(R+r), constante de temps du dipôle.

di/dt +1/ t i = E/L (1)

Solution générale de l'équation sans second membre : i(t) = A exp(-t/ t).

Solution particulière de (1), régime permanent : I= E/(R+r).

Solution générale de l'équation de (1) : i(t) = A exp(-t/ t) +E/(R+r).

A t=0, l'intensité est nulle d'où : 0 = A+E/(R+r) soit A = -E/(R+r)

i(t) = E/(R+r)[1-exp(-t/ t)].
Préciser les unités usuelles des différentes grandeurs utilisées.

i : intensité (A) ; E : f.e.m du générateur (V)

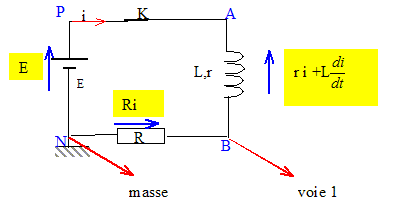
R, r : résistance (W) ; L : inductance (H)

t : temps (s)
On désire visualiser en voie A d’un oscilloscope les variations de l’intensité en fonction du temps.

Indiquer les branchements à effectuer. Justifier.

L'intensité qui traverse un résistor et la tension à ses bornes sont proportionnelles ;

visualiser la tension aux bornes d'un résistor, c'est voir l'image de l'intensité au facteur R près.
 


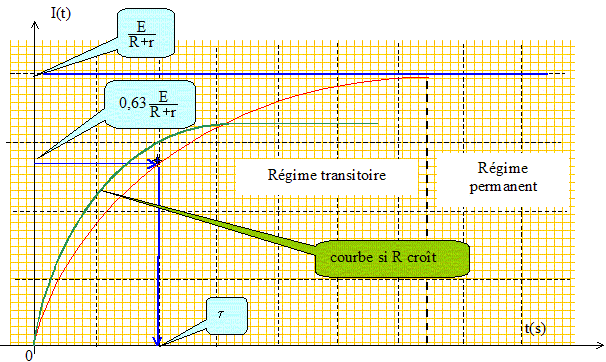
Etablir l’expression de l’intensité I du courant lorsque le régime permanent est établi dans le circuit.

En régime permanent di/dt =0 d'où, d'après (1) : I=E/(R+r).

La constante de temps du circuit est t = L / (R + r) .

Montrer que t est homogène au temps.

Energie stockée dans la bobine : E= ½LI2 soit L= 2E / I2.

Energie dissipée par effet Joule dans la résistance R+r : E = (R+r)I2t soit R+r = E/(I2t).

En conséquence L/(R+r) a la dimension d'un temps.

Tracer l’allure de la fonction i(t) en faisant apparaître la constante de temps, la fin du régime transitoire et la valeur caractéristique de l’intensité en fonction de sa valeur maximale.

Préciser comment évolue cette courbe si R augmente, la nouvelle valeur permettant de négliger r .

Si R augmente la constante de temps diminue. Le régime permanent est plus rapidement atteint ; l'intensité en régime permanent diminue.

Donner l’expression de l’énergie magnétique emmagasinée par la bobine lorsque le régime permanent est établi.

Energie= ½LI2 avec I= E/(R+r)

Energie = ½L[E/(R+r)]2.

 


retour -menu