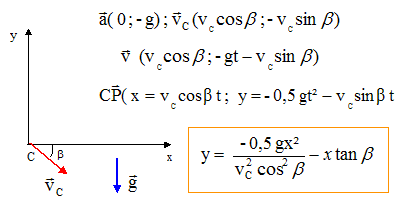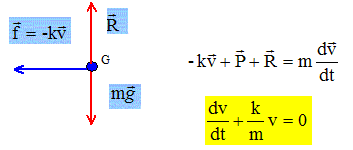acide butyrique, tremplin de saut à ski concours ingénieur Geipi ENI 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

L’acide butyrique, de formule semi développée CH3-CH2-CH2-COOH, est connu pour son odeur désagréable de beurre rance. Sa réaction avec le méthanol (CH3OH) permet d’obtenir un composé E, dont l’odeur et le goût sont au contraire très agréables, d’où son utilisation dans l’industrie alimentaire ou la parfumerie. Donner le nom systématique de l’acide butyrique. Acide butanoïque. Ecrire l’équation bilan de la réaction entre l’acide butyrique et le méthanol. CH3-CH2-CH2-COOH + CH3OH = CH3-CH2-CH2-COO -CH3 + H2O. Donner le nom de la fonction chimique caractéristique du composé E. Nommer E. ester : butanoate de méthyle. On souhaite réaliser la synthèse du composé E ; pour cela, on dispose d’une masse mA = 330 g d’acide butyrique. Calculer la masse de méthanol qu’il faut mettre en oeuvre pour mener la réaction dans des conditions stoechiométriques. M(acide butyrique) =4*12+8+2*16 = 88 g/mol n = mA/M = 330/88 =3,75 mol. M(méthanol) = 12+4+16 =32 g/mol. Masse de méthanol : 3,75*32 =120 g. L’acide butyrique et le méthanol sont introduits dans le réacteur et le mélange est porté à ébullition. Le volume total est V = 400 mL. Il est possible de suivre l’évolution de la réaction par le dosage de l’acide butyrique restant. Pour ce faire, on réalise périodiquement des prélèvements de 1,00 mL du mélange réactionnel. Chaque prélèvement est alors dilué dans de l’eau glacée, puis dosé par une solution de soude à 0,20 mol.L-1. Ecrire la réaction de dosage de l’acide butyrique par la soude. CH3-CH2-CH2-COOH + HO- = CH3-CH2-CH2-COO- + H2O.     Calculer la constante d’équilibre de la réaction de dosage. pKa( CH3-CH2-CH2-COOH / CH3-CH2-CH2-COO- ) =4,9. K = [CH3-CH2-CH2-COO- ] / ([CH3-CH2-CH2-COOH][HO-]) Or Ka = [CH3-CH2-CH2-COO- ] [H3O+] / [CH3-CH2-CH2-COOH] soit [CH3-CH2-CH2-COOH] / [CH3-CH2-CH2-COO- ] = Ka /[H3O+] par suite K s'écrit : K = Ka / ([H3O+][HO-]) =Ka /Ke = 10-4,9/10-14 = 109,1 =1,3 109. Quel volume de soude faut-il verser pour doser l’acide du premier prélèvement à t = 0 ? A l'équivalence les quantités de matière de réactifs mis en présence sont en proportions stoechiométriques : CaVa= CbVb ; Vb = CaVa/ Cb avec Ca = 3,75/0,4 = 9,375 mol/L ; Va= 1 mL ; Cb = 0,2 mol/L Vb = 9,375*1/0,2 =46,9 mL ~ 47 mL. Au bout de 120 heures, le système n’évolue plus ; les dosages à la soude permettent de déterminer l’avancement de la réaction : xmax = 2,50 mol. Calculer le rendement en produit E par rapport à la quantité de réactif de départ. h = xmax / ninitial / =2,50/3,75= 0,667 ( 66,7 % ) Il est recommandé, pour mener ce type de réaction, d’ajouter quelques millilitres d’acide sulfurique au mélange réactionnel. Préciser le rôle de l’acide sulfurique dans la réaction chimique : Obtenir un meilleur rendement en E ; rendre la réaction moins explosive ; rendre la réaction réversible ; augmenter l'avancement maximal ; diminuer le temps de demi-réaction ; empécher la formation de produits secondaires ; neutralyser l'acide butyrique ; détruire le méthanol.   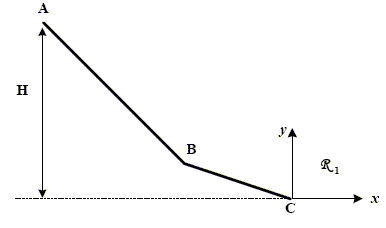Tremplin de saut à ski. On considère un petit tremplin de saut a ski dont le profil est présente sur la figure suivante. Il est techniquement constitué de trois zones : - une zône linéaire AB dont l'angle a par rapport a l'fhorizontale est égal à 45�°, - une zône circulaire de raccordement, - une seconde zône linéaire BC dont l'angle b par rapport a l'horizontale est égal à 30°. Le point de sortie C du tremplin est situe à une hauteur H par rapport à la cabine de départ. On supposera que le frottement des skis sur la piste du tremplin est négligeable et on néglige les frottements de l'air durant cette premiere phase du saut. Le skieur est considére comme un objet ponctuel de masse m = 75 kg. On donne l'accélération de pesanteur g = 9,80 m.s-2. On étudie l’envol du skieur. En appliquant la loi de conservation de l’énergie, donnez l’expression littérale du module de la vitesse VC au point C. En A l'énergie mécanique est sous forme potentielle de pesanteur : mgH. En C l'énergie mécanique est sous forme cinétique : ½mVC2. Conservation de l'énergie mécanique : mgH = ½mVC2 VC = [2gH]½. Quelle doit être la hauteur H pour que VC = 14 m.s-1 ? H =0,5 VC2 / g = 0,5*142/9,80 =10 m. Quel est l’angle de sortie lorsque le skieur s’élance du tremplin ? b=30°. Etablissez les équations horaires x(t) et y(t) du mouvement du skieur dans sa phase d’envol, dans le repère R1(C,x,y) en fixant t = 0 lorsque le skieur atteint le point C. Donnez l’expression y = f(x) de la trajectoire du skieur. 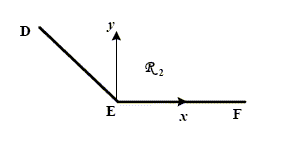Le skieur se réceptionne sur la partie DE. La zone d’arrêt EF comporte en surface des éléments qui permettent de ralentir le skieur. On supposera par ailleurs que le frottement de l’air n’est plus négligeable. On modélisera les effets du frottement par une force unique dont le module f est proportionnel à la vitesse du skieur. On appellera k le coefficient de proportionnalité. On étudie le mouvement du skieur lorsqu’il a atteint la zone d’arrêt EF. On travaillera dans le repère R2(E,x,y) en fixant t=0 lorsque le skieur atteint le point E. Etablissez l’équation différentielle en vitesse du mouvement du skieur sur la zone d’arrêt. On vérifiera que la vitesse (dans cette portion de la piste) peut se mettre sous la forme : v(t) = v0 exp(-t/t). On identifiera t. dv/dt = -tv0 exp(-t/t) ; repport dans l'équation différentielle : -tv0 exp(-t/t) + k/mv0 exp(-t/t) =0 égalité vérifiée quel que soit t si t = m/k. Le skieur a-t-il une chance de s'arrêter si l'on tient compte de cette seule expression de la vitesse ? Pourquoi ? Le skieur s'arrêterra à une date un peu supérieure à 5t ; si t est grand, il risque de ne pas s'arrêter à temps. Il faudrait penser à un autre modèle pour la force de frottement.

retour -menu